In example above, find the potential difference between points F and C.
To find the potential difference between points F and C, we will use Kirchhoff's laws to analyze the circuit. Here’s a step-by-step solution:
Step 1: Apply Kirchhoff's Second Law
We start by applying Kirchhoff's second law in the loop that includes points A, B, E, and F.
1. Assume the current flowing through the circuit is I.
2. The voltage drops and rises in the loop can be expressed as:
−4I+4+4−2I=0
Here, −4I is the voltage drop across a 4-ohm resistor, and +4 and +2 are the voltage rises from the sources.
Step 2: Simplify the Equation
Combine the terms:
−6I+6=0
From this, we can solve for I:
6I=6⟹I=1A
Step 3: Split the Current
Next, we note that the current I splits into two branches at point E, denoting them as I1 and I2.
Step 4: Apply Kirchhoff's Law in the Second Loop
We apply Kirchhoff's law in the loop that includes points E, F, and C:
−2I2−6−4I2−4=0
Combine the terms:
−6I2−10=0
From this, we can solve for I2:
6I2=−10⟹I2=−53A
Step 5: Find I1
Using the relationship I=I1+I2:
1=I1−53
Solving for I1:
I1=1+53=83A
Step 6: Calculate the Potential Difference VF−VC
Now we need to find the potential difference between points F and C. We apply Kirchhoff's law in the loop F, A, B, C:
VF−VC=2+(−4I)+(−2I2)
Substituting the values we have:
VF−VC=2−4(1)−2(−53)
Calculating this:
=2−4+103=−2+103=−2+103=−6+103=43V
Final Answer
Thus, the potential difference between points F and C is:
VF−VC=−43V
We start by applying Kirchhoff's second law in the loop that includes points A, B, E, and F.
2. The voltage drops and rises in the loop can be expressed as:
−4I+4+4−2I=0
Here, −4I is the voltage drop across a 4-ohm resistor, and +4 and +2 are the voltage rises from the sources.
Combine the terms:
−6I+6=0
From this, we can solve for I:
6I=6⟹I=1A
Next, we note that the current I splits into two branches at point E, denoting them as I1 and I2.
We apply Kirchhoff's law in the loop that includes points E, F, and C:
−2I2−6−4I2−4=0
Combine the terms:
−6I2−10=0
From this, we can solve for I2:
6I2=−10⟹I2=−53A
Using the relationship I=I1+I2:
1=I1−53
Solving for I1:
I1=1+53=83A
Now we need to find the potential difference between points F and C. We apply Kirchhoff's law in the loop F, A, B, C:
VF−VC=2+(−4I)+(−2I2)
Substituting the values we have:
VF−VC=2−4(1)−2(−53)
Calculating this:
=2−4+103=−2+103=−2+103=−6+103=43V
Thus, the potential difference between points F and C is:
VF−VC=−43V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
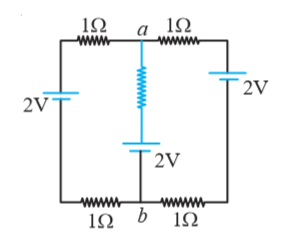
Find theh potential difference between points a and b.
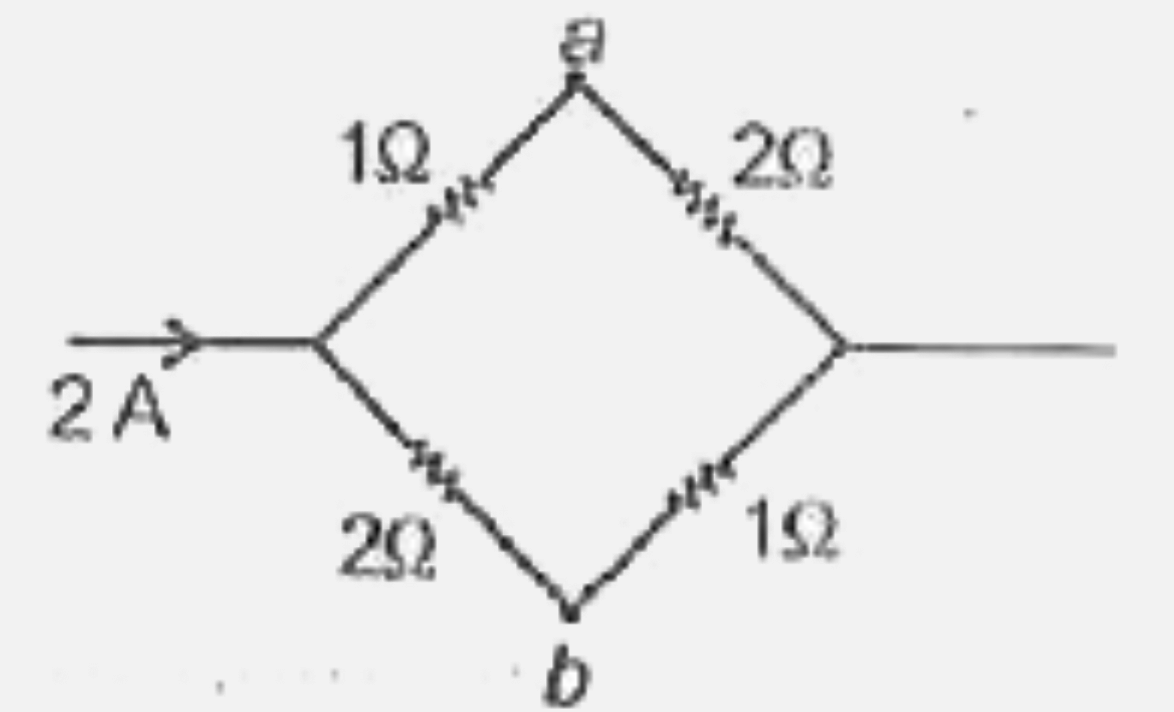
View SolutionThe potential difference between points A and B is
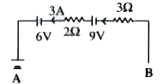
View SolutionThe potential difference between points A and B is
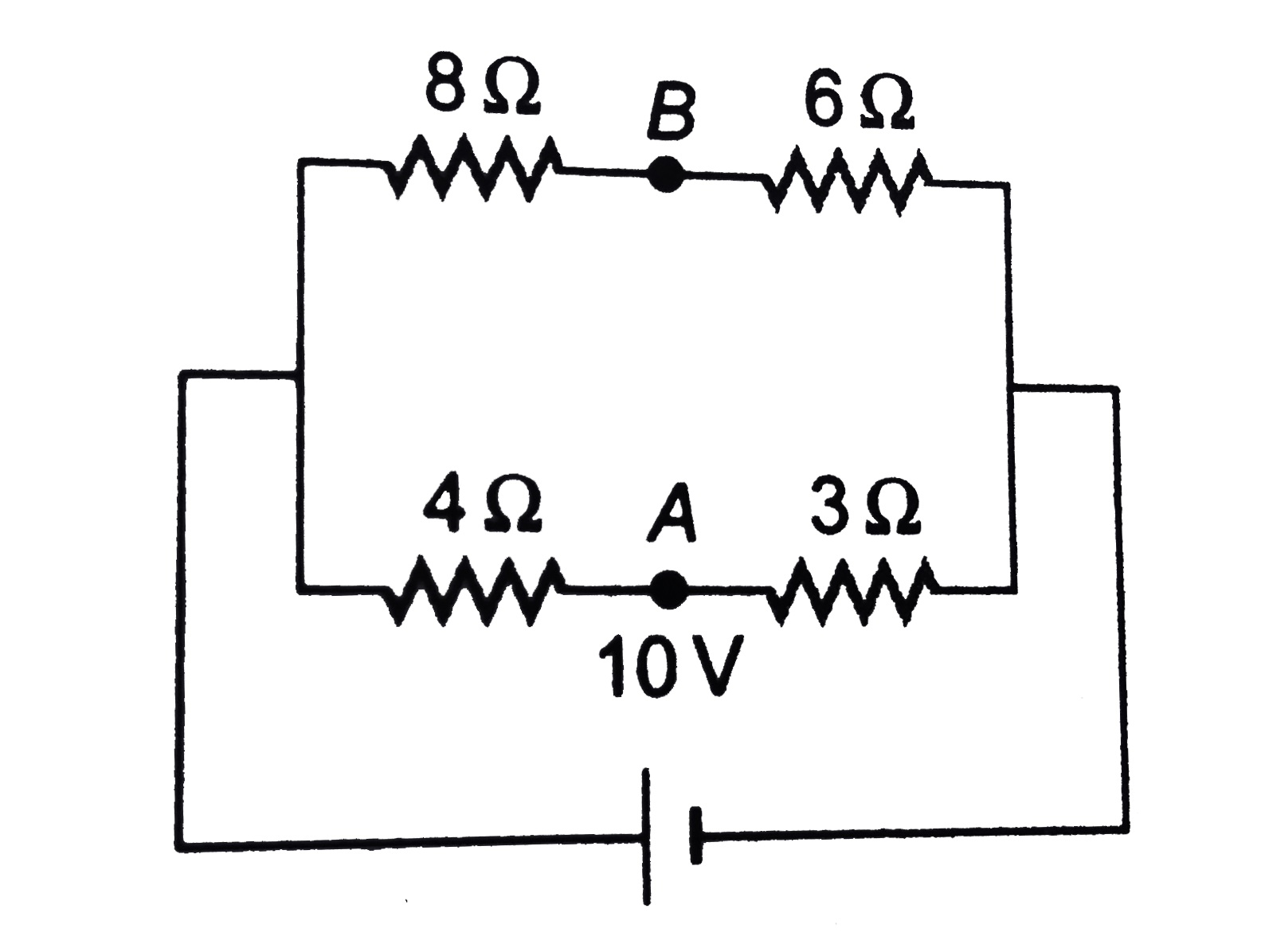
View SolutionThe potential difference between points A and B is

View Solution(i) Find the potential difference between A and B.

View SolutionZeta potential is the potential difference between
View SolutionIn the diagram shown find the potential difference between the points A and B and between the points B and C in the steady state.
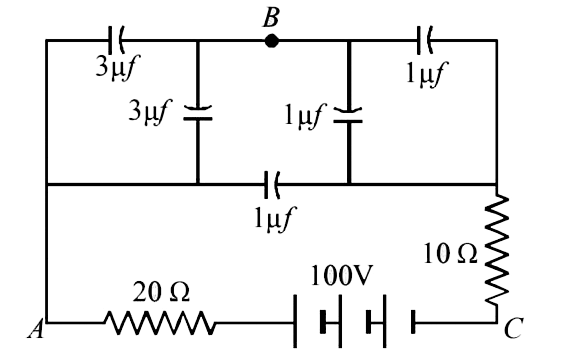
View SolutionFor the circuit in find the potential difference between points a and b.
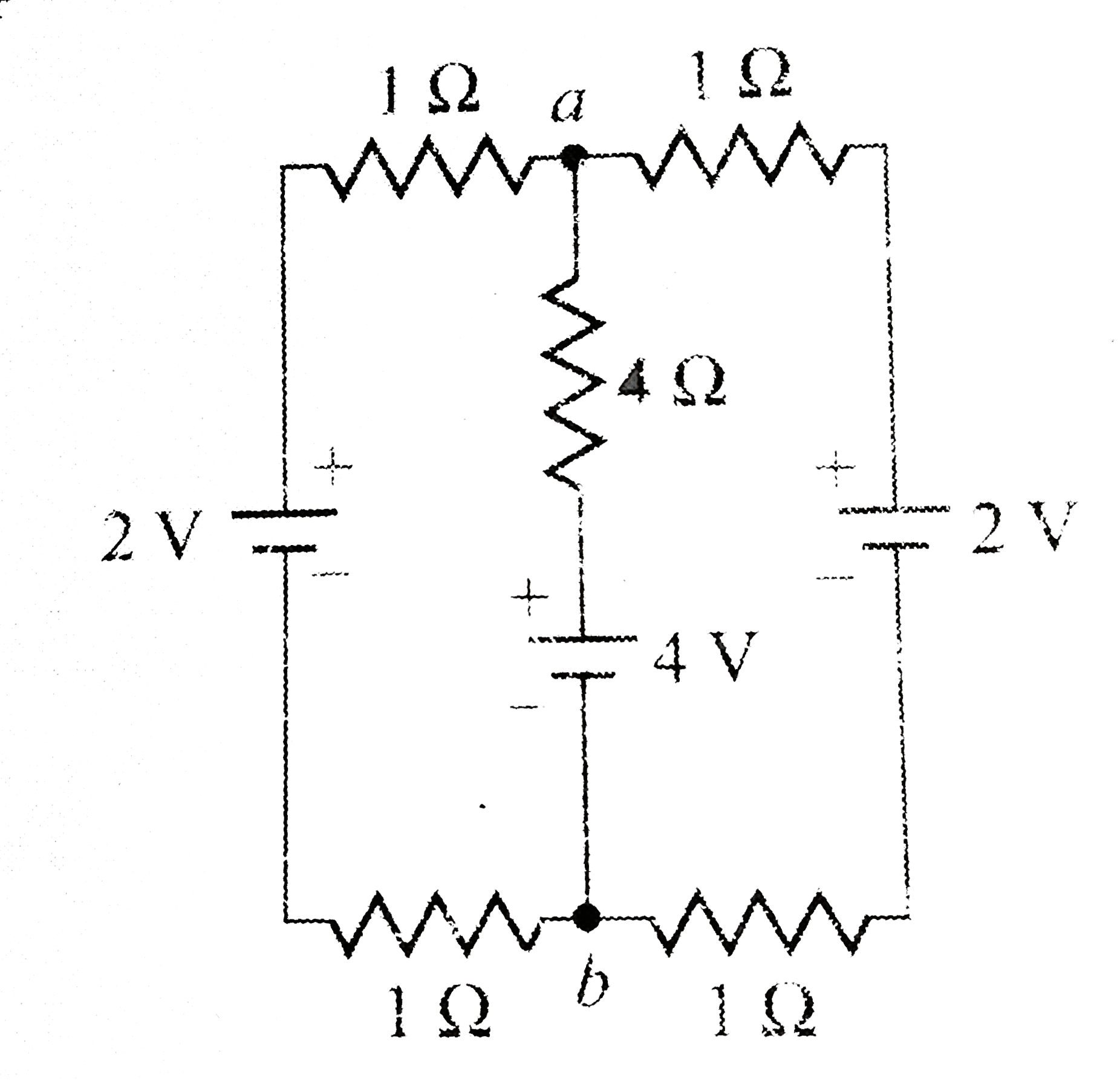
View SolutionFor the circuit figure, find the potential difference between points a and b:
View SolutionThe potential difference between points A and B adjoining figure is
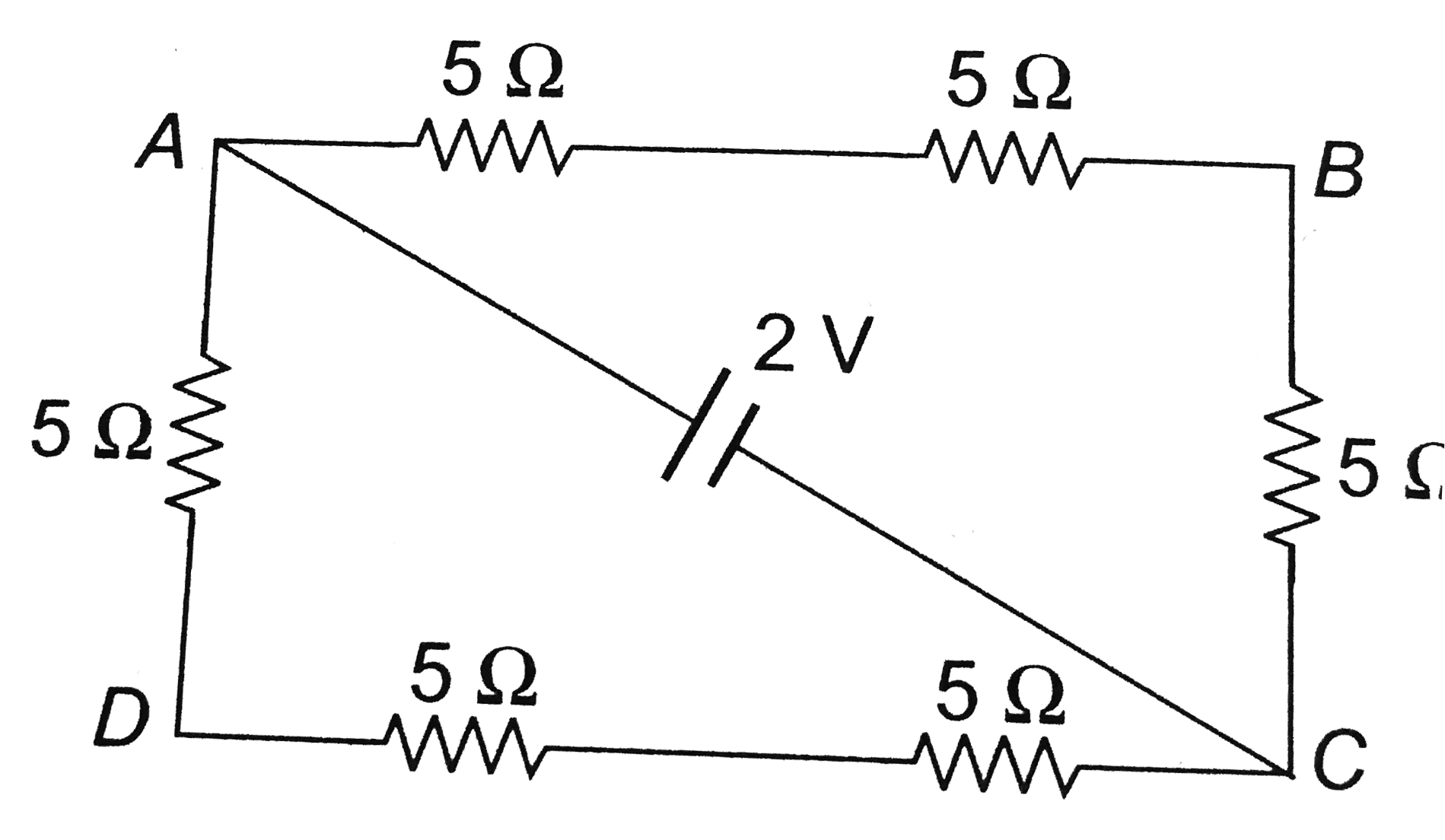
View Solution
