A beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Find the magnification and nature of the image when point O is 10cm behind the mirror.
2(virtual,inverted)
3(real, inverted)
5(virtual, enlarged)
2 (real, erect)
The correct Answer is:d.
To solve the problem step by step, we will use the mirror formula and the magnification formula for a convex mirror.
Step 1: Identify the given values
- Focal length of the convex mirror (F) = +20 cm (positive for convex mirrors)
- Distance of the point O behind the mirror (u) = -10 cm (negative because the object is virtual and located behind the mirror)
Step 2: Use the mirror formula
The mirror formula is given by:
1f=1v+1u
Substituting the known values into the formula:
120=1v+1−10
Step 3: Rearranging the equation
Rearranging the equation gives:
1v=120+110
To add these fractions, we need a common denominator. The common denominator for 20 and 10 is 20:
1v=120+220=320
Step 4: Solve for v
Now, taking the reciprocal to find v:
v=203≈6.67 cm
Since v is positive, this indicates that the image is formed on the same side as the object (in front of the mirror).
Step 5: Find the magnification (m)
The magnification (m) is given by the formula:
m=−vu
Substituting the values we found:
m=−6.67−10=6.6710=0.667
Step 6: Determine the nature of the image
Since the magnification is positive, the image is erect. The value of magnification being less than 1 indicates that the image is smaller than the object.
Final Results
- The image distance (v) is approximately 6.67 cm in front of the mirror.
- The magnification (m) is approximately 0.667, indicating that the image is erect and smaller than the object.
- Focal length of the convex mirror (F) = +20 cm (positive for convex mirrors)
- Distance of the point O behind the mirror (u) = -10 cm (negative because the object is virtual and located behind the mirror)
The mirror formula is given by:
1f=1v+1u
Substituting the known values into the formula:
120=1v+1−10
Rearranging the equation gives:
1v=120+110
To add these fractions, we need a common denominator. The common denominator for 20 and 10 is 20:
1v=120+220=320
Now, taking the reciprocal to find v:
v=203≈6.67 cm
Since v is positive, this indicates that the image is formed on the same side as the object (in front of the mirror).
The magnification (m) is given by the formula:
m=−vu
Substituting the values we found:
m=−6.67−10=6.6710=0.667
Since the magnification is positive, the image is erect. The value of magnification being less than 1 indicates that the image is smaller than the object.
- The image distance (v) is approximately 6.67 cm in front of the mirror.
- The magnification (m) is approximately 0.667, indicating that the image is erect and smaller than the object.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Similarly, as in above question when point O is 30cm behind the mirror.View SolutionA body of length 6 cm is placed 10cm from a concave mirror of focal length 20cm. Find the position, size, and nature of the image.
View SolutionAn object of height 2 cm is placed at a distance 20cm in front of a concave mirror of focal length 12 cm. Find the position, size and nature of the image
View SolutionObject is placed 15 cm from a concave mirror of focal length 10 cm, then the nature of the image formed will be
View SolutionObject is placed 15 cm from a concave mirror of focal length 10 cm, then the nature of the image formed will be
View Solutiona. An object 1 cm high is placed at 10cm in front of a concave mirror of focal length 15 cm. Find the position, height, and nature of the image.
b. A point source S is placed midway between two converging mirrors having equal focal length f as shown in Figure. Find the value of d for which only one image is formed.
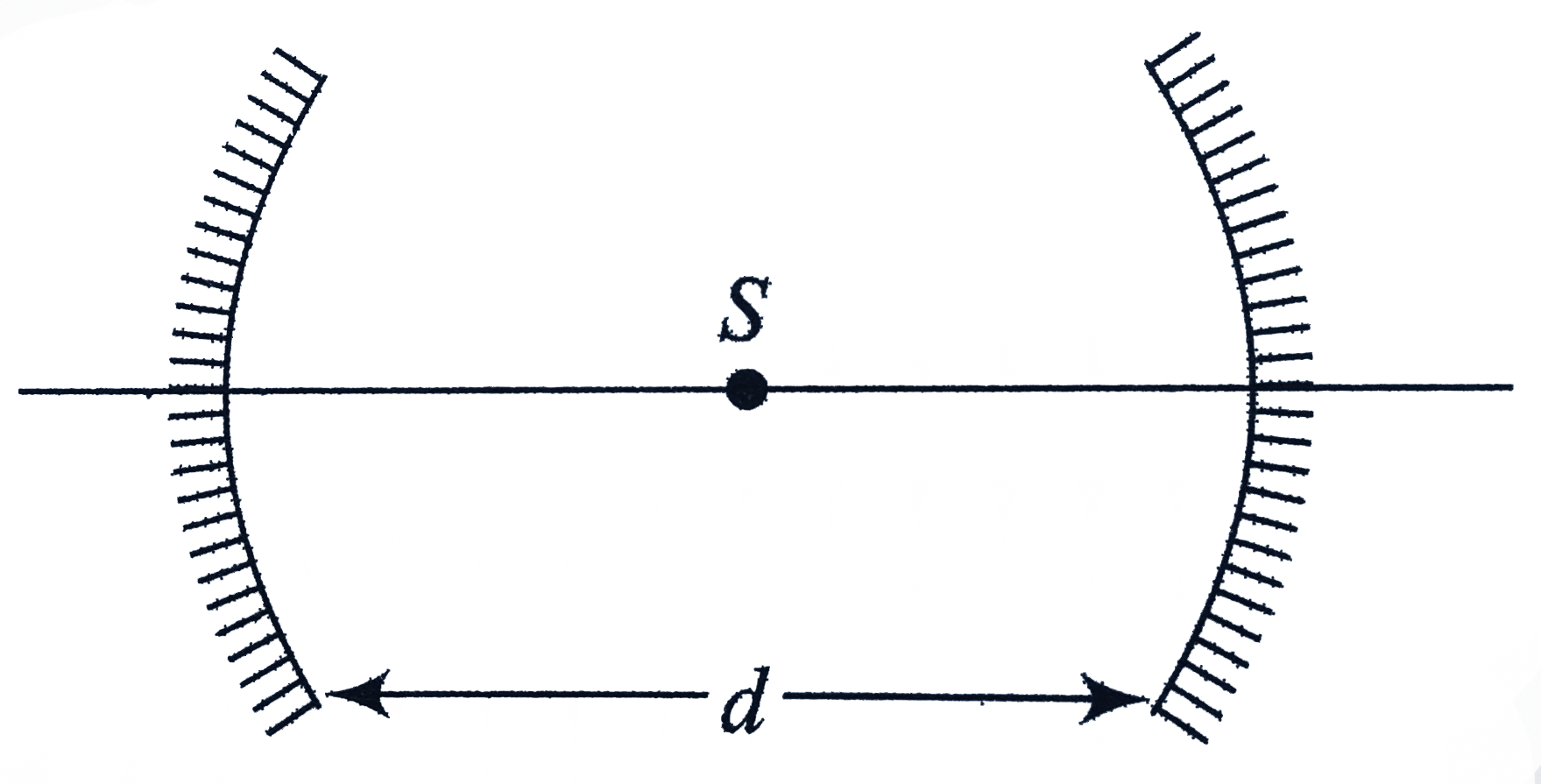 View Solution
View SolutionAn object 10 mm high is placed 30 cm from a convex mirror whose focal length is 20 cm. Find the position (in cm), size (in mm) and nature of the image.
View SolutionAn object is at 20 cm from a concave mirror of focal length 10 cm, the nature of image is
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by a mirror is
View Solution

