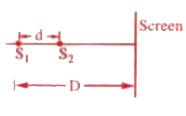
In Young's doulbe-slit experiment the separation between two coherent sources $S_{1}$ and $S_{2}$ is d and the distance between the source and screen is D. In the interference pattern, it is found that exactly in front of one slit, there occurs a minimum. Then the possible wavelengths used in the experiment are

A

$λ = \frac{d^{2}}{D}, \frac{d^{2}}{3 D}, \frac{d^{2}}{5 D}$

B

$λ = \frac{d^{2}}{D}, \frac{d^{2}}{5 D}, \frac{d^{2}}{9 D}$

C

$λ = \frac{d^{2}}{D}, \frac{d^{2}}{2 D}, \frac{d^{2}}{3 D}$

D

$λ = \frac{d^{2}}{3 D}, \frac{d^{2}}{7 D}, \frac{d^{2}}{11 D}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

$y = \frac{d}{2} = \frac{2 (n - 1) D λ}{2 d}$
$\Rightarrow λ = \frac{d^{2}}{D (n - 1)}, n = 1, 2, 3$

Updated on:21/07/2023

|

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

In Young's double slit experiment, the distance d between the slits $S_{1}$ and $S_{2}$ is 1 mm. What should the width of each slit be so as to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern ?
A0.9 mm
B0.8 mm
C0.2 mm
D0.6 mm

CENGAGE PHYSICS ENGLISH-WAVE OPTICS-Single Correct

Home
Ask Doubt
Profile