A π−meason hydrogen atom is a bound state of negative charged pion (denoted by π¯,mπ=273me) and a proton. Estimate the number of revolutions a π−meason makes (averagely ) in the ground state on the atom before , it decays (mean life of a π−meason≅10−8s, mass of proton =1.67×10−27kg).
The correct Answer is:1.77×1010 revolutions
To estimate the number of revolutions a pi meson makes in a hydrogen atom before it decays, we can follow these steps:
Step 1: Understand the Problem
We have a pi meson (negative charged pion) with a mass of mπ=273me (where me is the mass of the electron) and a proton. The mean life of the pi meson is given as τ=10−8 seconds. We need to find out how many revolutions it makes before it decays.
Step 2: Calculate the Reduced Mass
The reduced mass μ of the system (pi meson and proton) is calculated using the formula:
μ=mπmpmπ+mp
Where:
- mπ=273me
- mp=1.67×10−27 kg
- me=9.1×10−31 kg
Substituting the values:
μ=(273×9.1×10−31)(1.67×10−27)(273×9.1×10−31)+(1.67×10−27)
Step 3: Calculate the Frequency of Revolution
The frequency f of the pi meson in a hydrogen-like atom can be expressed as:
f=4π2k2e4μh2
Where:
- k=14πϵ0≈9×109N m2/C2
- e=1.6×10−19C (charge of the electron)
- h=6.63×10−34Js (Planck's constant)
Substituting the reduced mass μ calculated in Step 2 into the frequency formula.
Step 4: Calculate the Total Number of Revolutions
The total number of revolutions N before the pi meson decays can be calculated as:
N=f⋅τ
Where τ=10−8 seconds is the mean life of the pi meson.
Step 5: Final Calculation
After calculating f and substituting it into the equation for N, we can find the total number of revolutions.
Solution Summary
1. Calculate the reduced mass μ.
2. Calculate the frequency f using the reduced mass.
3. Calculate the total number of revolutions N using the mean life.
We have a pi meson (negative charged pion) with a mass of mπ=273me (where me is the mass of the electron) and a proton. The mean life of the pi meson is given as τ=10−8 seconds. We need to find out how many revolutions it makes before it decays.
The reduced mass μ of the system (pi meson and proton) is calculated using the formula:
μ=mπmpmπ+mp
Where:
- mπ=273me
- mp=1.67×10−27 kg
- me=9.1×10−31 kg
μ=(273×9.1×10−31)(1.67×10−27)(273×9.1×10−31)+(1.67×10−27)
The frequency f of the pi meson in a hydrogen-like atom can be expressed as:
f=4π2k2e4μh2
Where:
- k=14πϵ0≈9×109N m2/C2
- e=1.6×10−19C (charge of the electron)
- h=6.63×10−34Js (Planck's constant)
The total number of revolutions N before the pi meson decays can be calculated as:
N=f⋅τ
Where τ=10−8 seconds is the mean life of the pi meson.
After calculating f and substituting it into the equation for N, we can find the total number of revolutions.
1. Calculate the reduced mass μ.
2. Calculate the frequency f using the reduced mass.
3. Calculate the total number of revolutions N using the mean life.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Single Correct187videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct13videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.212videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct10videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
Similar Questions
An isolated hydrogen atom emits a photon of 10.2eV.
(i) Determine the momentum of photon emitted (ii) Calculate the recoil momentum of the atom
(iii) Find the kinetic energy of the recoil atom [Mass of proton =mp=1.67×10−27kg]View SolutionA hydrogen atom in its ground state is irradiated by light of wavelength 970Å Taking hc/e=1.237×10−6eV m and the ground state energy of hydrogen atom as −13.6eV the number of lines present in the emmission spectrum is
View Solution
Knowledge Check
- Question 1 - Select One
if muonic hydrogen atom is an atom in which a negatively charged muon (μ) of mass about 207me revolves around a proton, then first bohr radius of this atom is (re=0.53×10−10m)
A2.56×10−10mB2.56×10−11mC2.56×10−12mD2.56×10−13m
Calculate the wavelength ( in nanometer ) associated with a proton moving at 1.0×103 m/s (Mass of proton =1.67×10−27kg and h=6.63×10−34is) :
View SolutionA non-relativistic proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic fields with E=120kVm−1andB=50mT. Then the beam strikes a grounded target. Find the force which the beam acts on the target if the beam current is equal to i=0.8mA.
Mass of protons =1.67×10−27kg.View SolutionIf the average life time of an excited state of hydrogen is of the order of 10−8s, estimate how many rotations an electron makes when it is in the state n=2 and before it suffers a transition to staten=1(Bohrradiusa0=5.3×10−11m)?
View SolutionConsider a system containing a negatively charge poin (π,mπ=273∘me) orbital around a staionary nucleus of atomic number Z .The total energy (En) of ion is half of its potential energy (PEn) in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The longest wavelength radiation emitted in the emission spectrum when the pion de-excited from n=3 to ground state lies which of the following region ?View SolutionA neutron moving with a speed u strikes a hydrogen atom in ground state in ground toward it with the same speed Find the minimum speed of the neutron for which ineleastic (completely or perially) collision may take place .The mass of neutron = mass of hydrogen =1.67×10−27kg
View SolutionThe figure shows a region of length ‘l’ with a uniform magnetic field of 0.3 T in it and a proton entering the region with velocity 4×105 ms−1 making an angle 60∘ with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘l’ is close to (mass of proton =1.67×10−27 kg , charge of the proton =1.6×10−19 C )
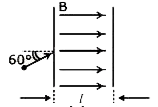 View Solution
View SolutionConsider a system containing a negatively charge poin (π,mπ=273∘me) orbital around a staionary nucleus of atomic number Z .The total energy (En) of ion is half of its potential energy (PEn) in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The wavelength (λn) of the pion orbital in nth stationarry state is ggiven by :View Solution

