A non-relativistic proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic fields with E=120kVm−1andB=50mT. Then the beam strikes a grounded target. Find the force which the beam acts on the target if the beam current is equal to i=0.8mA.
Mass of protons =1.67×10−27kg.
The correct Answer is:A, B
To solve the problem, we will follow these steps:
Step 1: Understand the conditions for the proton beam
The proton beam passes through a region with electric field E and magnetic field B without deviation. This means that the force due to the electric field is equal to the force due to the magnetic field.
Step 2: Set up the equation for force balance
The force due to the electric field FE is given by:
FE=qE
The force due to the magnetic field FB is given by:
FB=qvB
Setting these equal gives:
qE=qvB
We can cancel q (the charge of the proton) from both sides (as long as q≠0):
E=vB
Step 3: Solve for the velocity v
Rearranging the equation gives:
v=EB
Substituting the given values E=120×103V/m and B=50×10−3T:
v=120×10350×10−3=2.4×106m/s
Step 4: Calculate the number of protons hitting the target per second
The current I is related to the charge q and the number of protons n hitting the target per second:
I=nq
Where q (the charge of a proton) is approximately 1.6×10−19C. Rearranging gives:
n=Iq
Substituting I=0.8×10−3A:
n=0.8×10−31.6×10−19=5×1015protons/s
Step 5: Calculate the mass of protons hitting the target per second
The mass of the protons hitting the target per second is given by:
mass=n⋅mp
Where mp is the mass of a proton =1.67×10−27kg:
mass=5×1015⋅1.67×10−27=8.35×10−12kg
Step 6: Calculate the force acting on the target
The force F can be calculated using the change in momentum per unit time:
F=ΔpΔt=m⋅vt
Since we are considering 1 second:
F=mass⋅v
Substituting the values:
F=8.35×10−12⋅2.4×106=20×10−6N=20μN
Final Answer
The force with which the beam acts on the target is 20μN.
---
The proton beam passes through a region with electric field E and magnetic field B without deviation. This means that the force due to the electric field is equal to the force due to the magnetic field.
The force due to the electric field FE is given by:
FE=qE
The force due to the magnetic field FB is given by:
FB=qvB
Setting these equal gives:
qE=qvB
We can cancel q (the charge of the proton) from both sides (as long as q≠0):
E=vB
Rearranging the equation gives:
v=EB
Substituting the given values E=120×103V/m and B=50×10−3T:
v=120×10350×10−3=2.4×106m/s
The current I is related to the charge q and the number of protons n hitting the target per second:
I=nq
Where q (the charge of a proton) is approximately 1.6×10−19C. Rearranging gives:
n=Iq
Substituting I=0.8×10−3A:
n=0.8×10−31.6×10−19=5×1015protons/s
The mass of the protons hitting the target per second is given by:
mass=n⋅mp
Where mp is the mass of a proton =1.67×10−27kg:
mass=5×1015⋅1.67×10−27=8.35×10−12kg
The force F can be calculated using the change in momentum per unit time:
F=ΔpΔt=m⋅vt
Since we are considering 1 second:
F=mass⋅v
Substituting the values:
F=8.35×10−12⋅2.4×106=20×10−6N=20μN
The force with which the beam acts on the target is 20μN.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic field with E and B Then the beam strikes a grounded target. Find the force imparted by the beam on the target if the beam current is equal to I .
View SolutionNon-relativistic protons move reactilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields with E and B. The trajectory of the protons lie in the plane X-Y as shown in Fig. 1.107 and forms an angle ϕ with X-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.
 View Solution
View SolutionProtons move rectilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields E and B. The trajectory of protons lies in the plane xz as shown in the figure and forms an angle 9 with x-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.
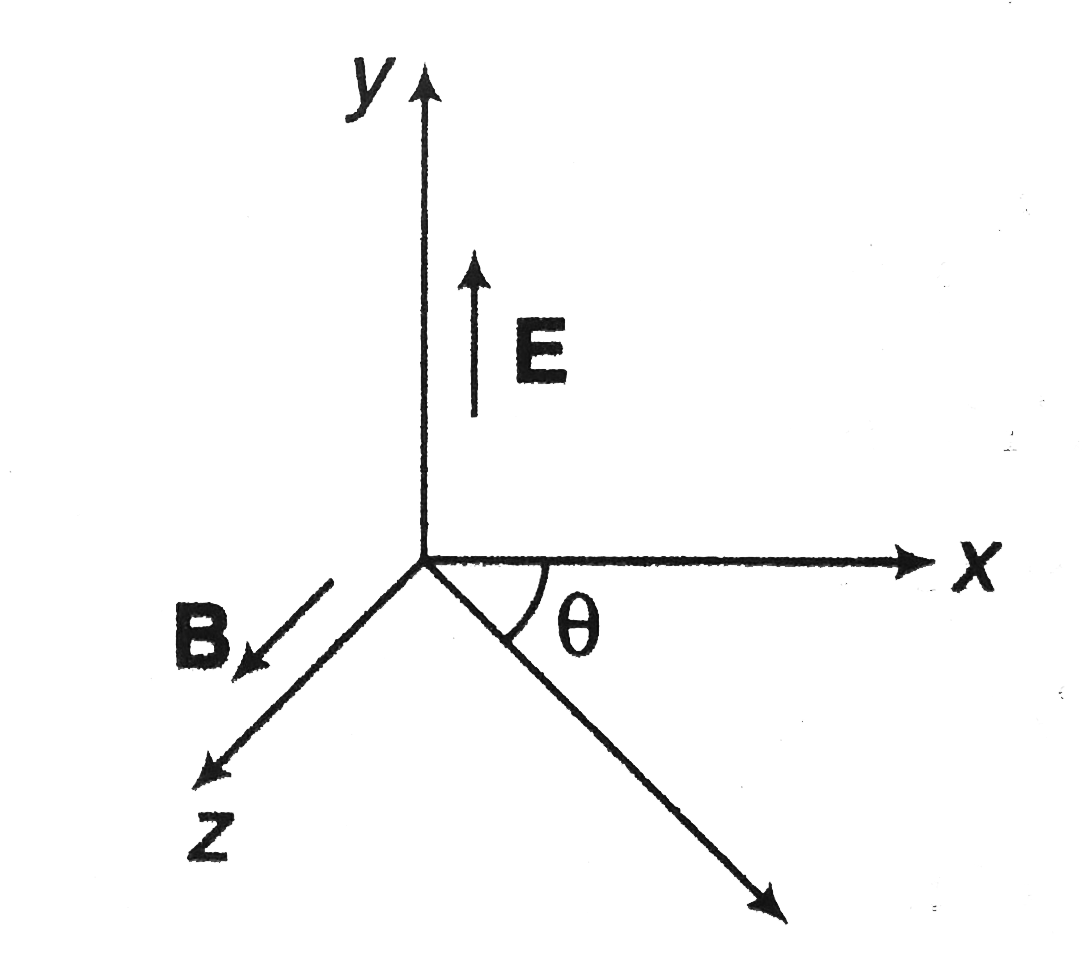 View Solution
View SolutionThere is a constant homogeneous electric field of 100Vm−1 within the region x=0andx=0.167m pointing in x-direction. There is a constant homogeneous mangetic field B within the region x=0.167mandx=0.334m pointing in the z-direction. A proton at rest at the origin is released in positive x-direction. Find the minimum strength of the magnetic field B, so that the proton is detected back at x=0,y=0.167m. (mass of proton =1.67×10−27kg)
View SolutionA narrow beam of singley charged carbon ions, moving at a constant velocity of 6.0X104ms−1, is sent perpendicularly in a rectangular region having uniform magnetic field B=0.5 T . It is found that two beams emerge from the field in the backward derection, the separations from the incident beam being 3.0 cm and 3.5cm. Identify the isotopes persent in the ion beam. Take the mass of an ion = A(1.6X10−27 kg, where A is the mass number.
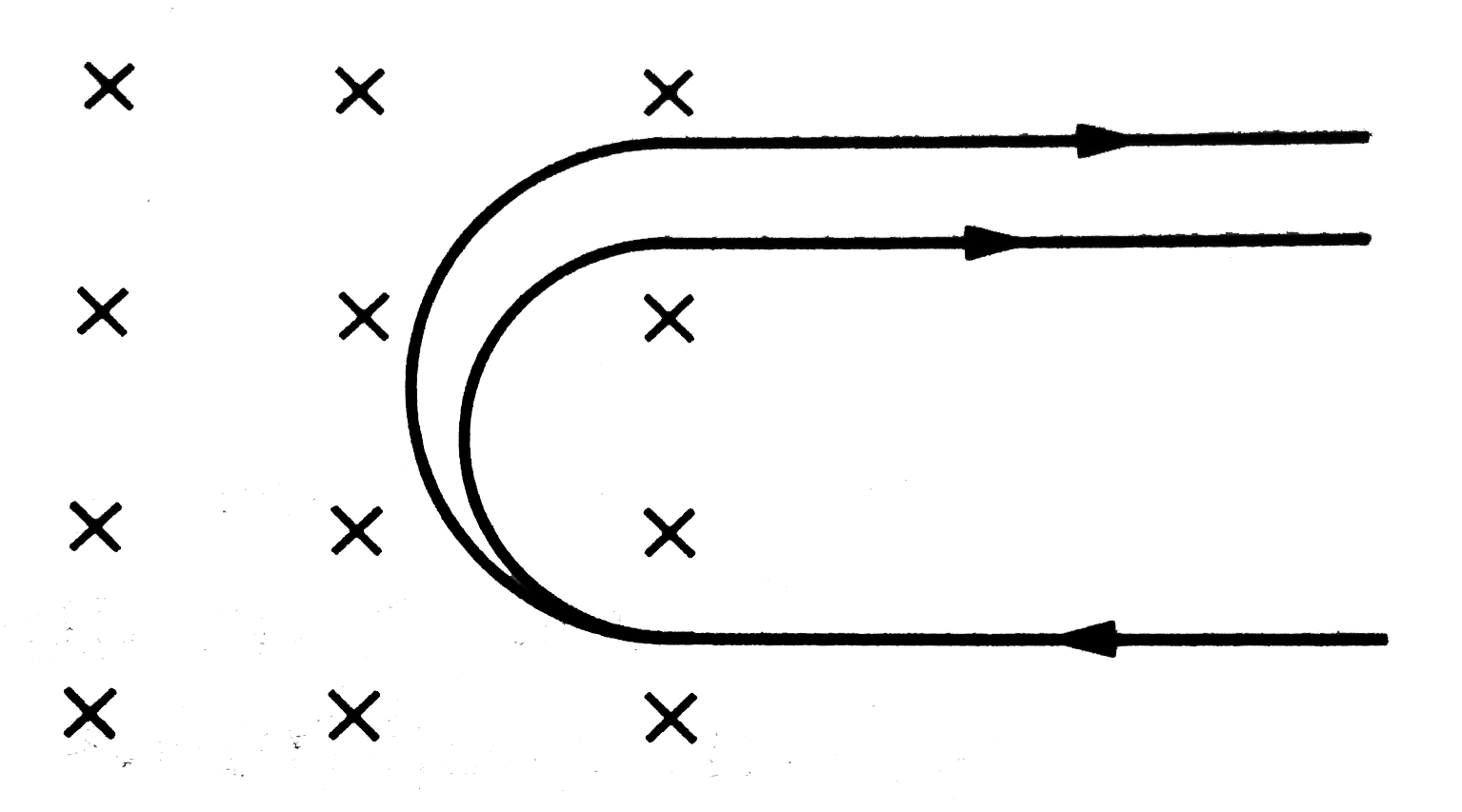 View Solution
View SolutionThe figure shows a region of length ‘l’ with a uniform magnetic field of 0.3 T in it and a proton entering the region with velocity 4×105 ms−1 making an angle 60∘ with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘l’ is close to (mass of proton =1.67×10−27 kg , charge of the proton =1.6×10−19 C )
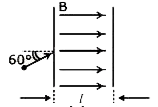 View Solution
View SolutionThe magnetic field in a certain region of space is given by B=8.35×10−2ˆiT.A proton is shot into the field with velocity v=(2×105ˆi+4×105ˆj)m/s. the proton follows a helical path in the field. The distance moved by proton in the x-direction during the period of one revolution in the yz-plane will be ( mass of proton=1.67×10−27kg)
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
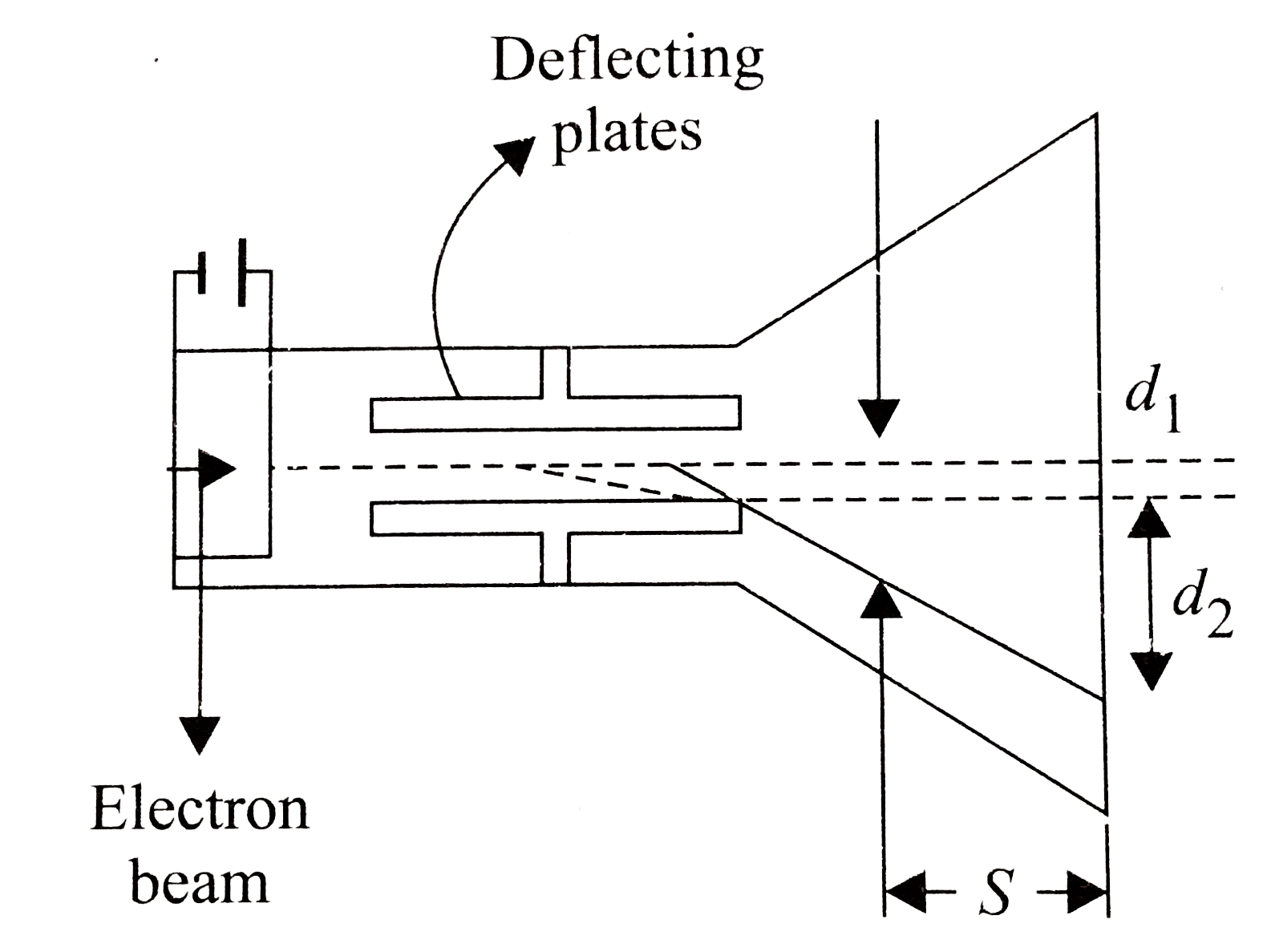
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron isView SolutionAn electron accelerated by a potential difference 2.5 kV moves horizontally into a region of space in which there is a downward directed uniform electric field of magnitude 10kVm−1.
(a) In what direction must a magnetic field be applied so that the electron moves undeflected? Ignore the gravitational force. What is the magnitude of the smallest magnetic field possible in this case?
(b) What happens if the charge is a proton that passes through the same combination of fields ?View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
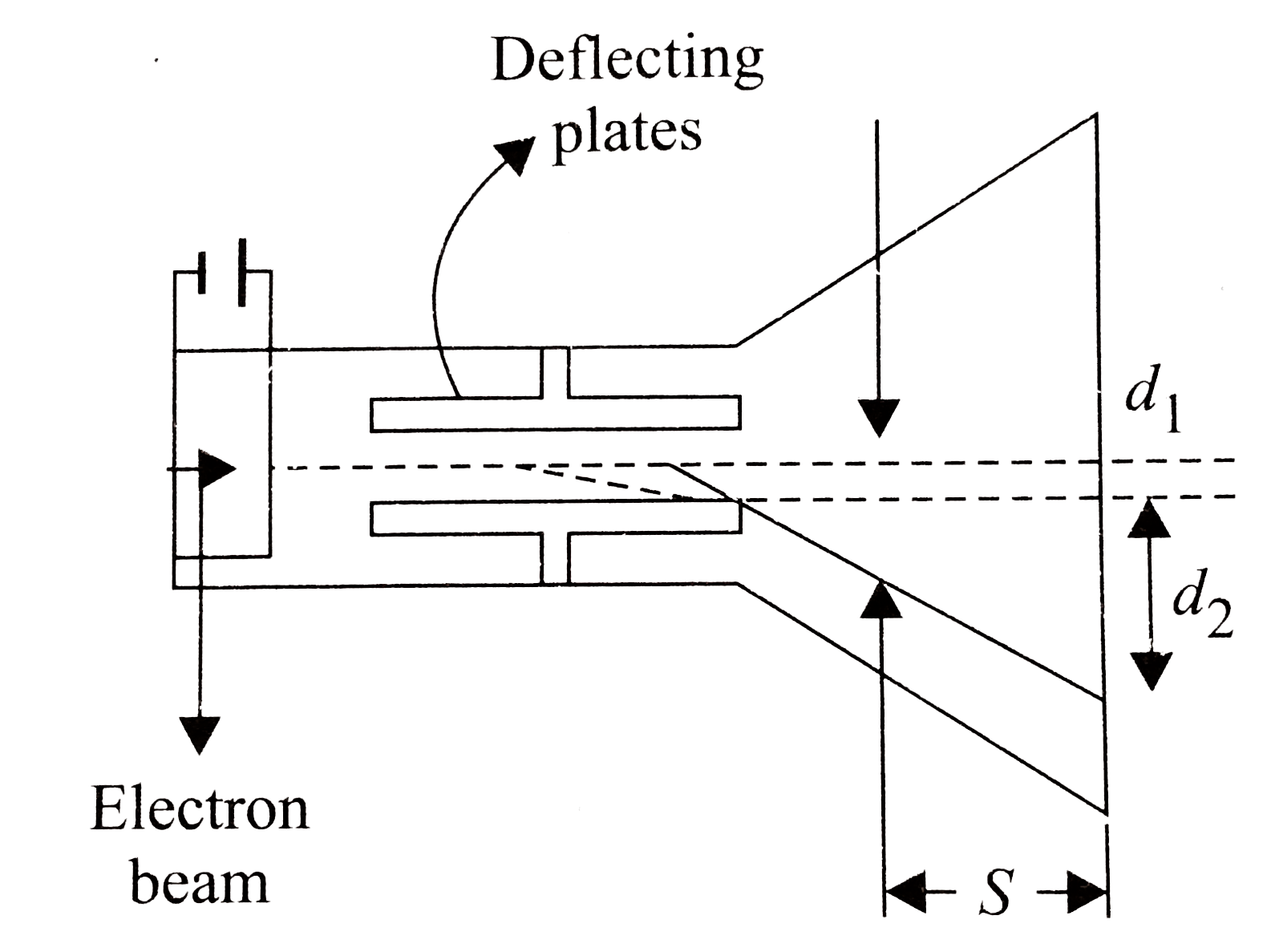
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experimentView Solution

