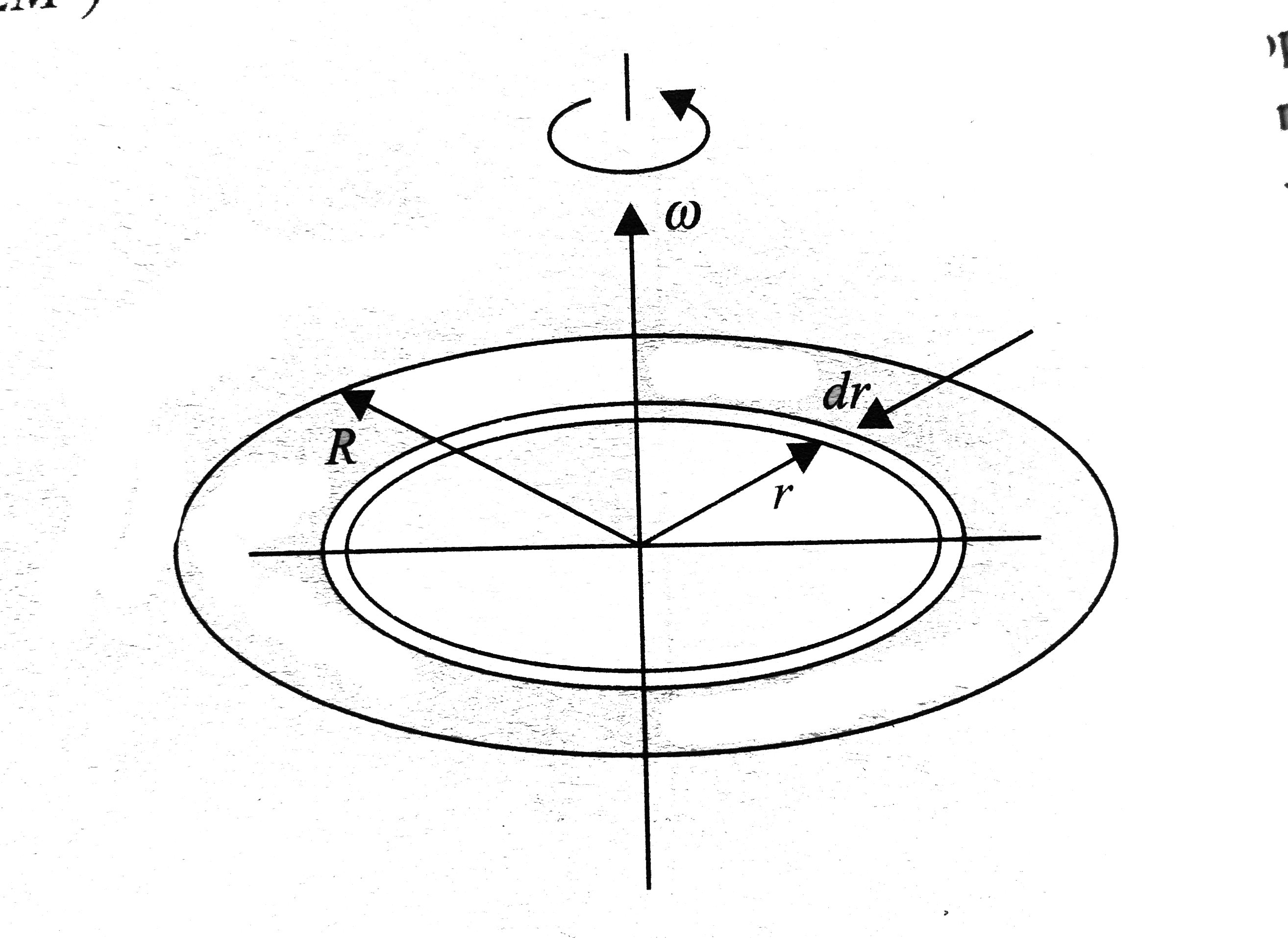
Consider a nonconducting plate of radius r and mass m which has a charge q distributed uniformly over it. The ring is rotated about its axis with an angular speed ω Show that the magnetic moment μ and the angular momentum I of the plate are rlated as μ=q2ml.
The charge is distributed on the surface of the disk.
We consider a differential ring of radius r and thickness dr.
The charge on the element is dq=σdA=σ(2πrdr)
The magnetic moment of the ring dμ=(dI)A=(dI)πr2
The current in the differential ring
dI=(dq)f=(σdA)ω2π=(σ2ωrdr)=σωrdr
The magnetic moment of the differential ring,
dμ(σωrdr)πr2=πσωr3dr
μ=∫dμ=∫R0πσωr3dr=14πσωR4
The magnetic vector →μ is parallel to →ω if charge is
positive.
→μ=14πσR4→ω
In terms of total charge Q=σπR2, the magnetic moment is
→μ=14QR2→ω
The angular momentum of disk is veL=(12MR2)→ω and
→μ=(Q2M)→L.
This is a general result for any rigid body of any arbitrary shape
having mass M and charge Q.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
Consider a non conducting plate of radius a and mass m which has a charge q distributed uniformly over it, The plate is rotated about its own axis with a angular speed ω. Show that the magnetic moment M and the angular momentum L of the plate are related as ML=q2m.
View SolutionConsider a non conducting plate of radius a and mass m which has a charge q distributed uniformly over it, The plate is rotated about its own axis with a angular speed ω. Show that the magnetic moment M and the angular momentum L of the plate are related as ML=q2m.
View Solutionconsider a nonconducting ring of radius r and mass m which has a total charge q distributed uniformly on it the ring is rotated about its axis with an angular speed ω. (a) Find the equivalent electric current in the ring (b) find the magnetic moment μ of the . (c) show thatμ=q2m where l is the angular momentum of the ring about its axis of rotation.
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View SolutionA thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity ω. Find the ratio of its magnetic moment and angular momentum.
View SolutionA thin circular disk of radius R is uniformly charged with density σ>0 per unit area.The disk rotates about its axis with a uniform angular speed ω.The magnetic moment of the disk is :
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
View SolutionThe ratio of magnetic dipole moment and angular momentum of charged body of charge q and mass m is
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution
