A particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

(a) The particle circulates under the influence of magnetic field. As the magnetic field is uniform , the charge comes out symmetrically. The angle subtended at the centre is (180−2θ).
(b) The length of the arc traced by the particle, l=R(π−2θ)
Time spent in the field, t=lv=R(π−2θ)v and R=mvBq
which gives t=mBq(π−2θ)
As time period: T=2πmBq, hence t=T2π(π−2θ)

we can generalize this result, If ϕ is the angle subtended by the arc traced by the charged particle is the magnetic field, the time spent is t=T(ϕ2π)
(c) Intercept EF=2Rcosθ.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercise 1.1
Explore 22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercise 1.2
Explore 13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Concept Based
Explore 8 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
Similar Questions
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B as shown in (a) Find The radius of the circular arc it describes in the magnetic field. (b) find the angle subtended by the arc at the center. (c ) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.

View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
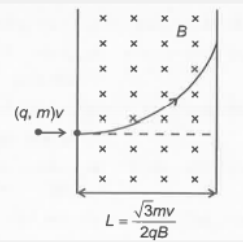
View SolutionA proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B.The radius of curvature of the resulting path is
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find
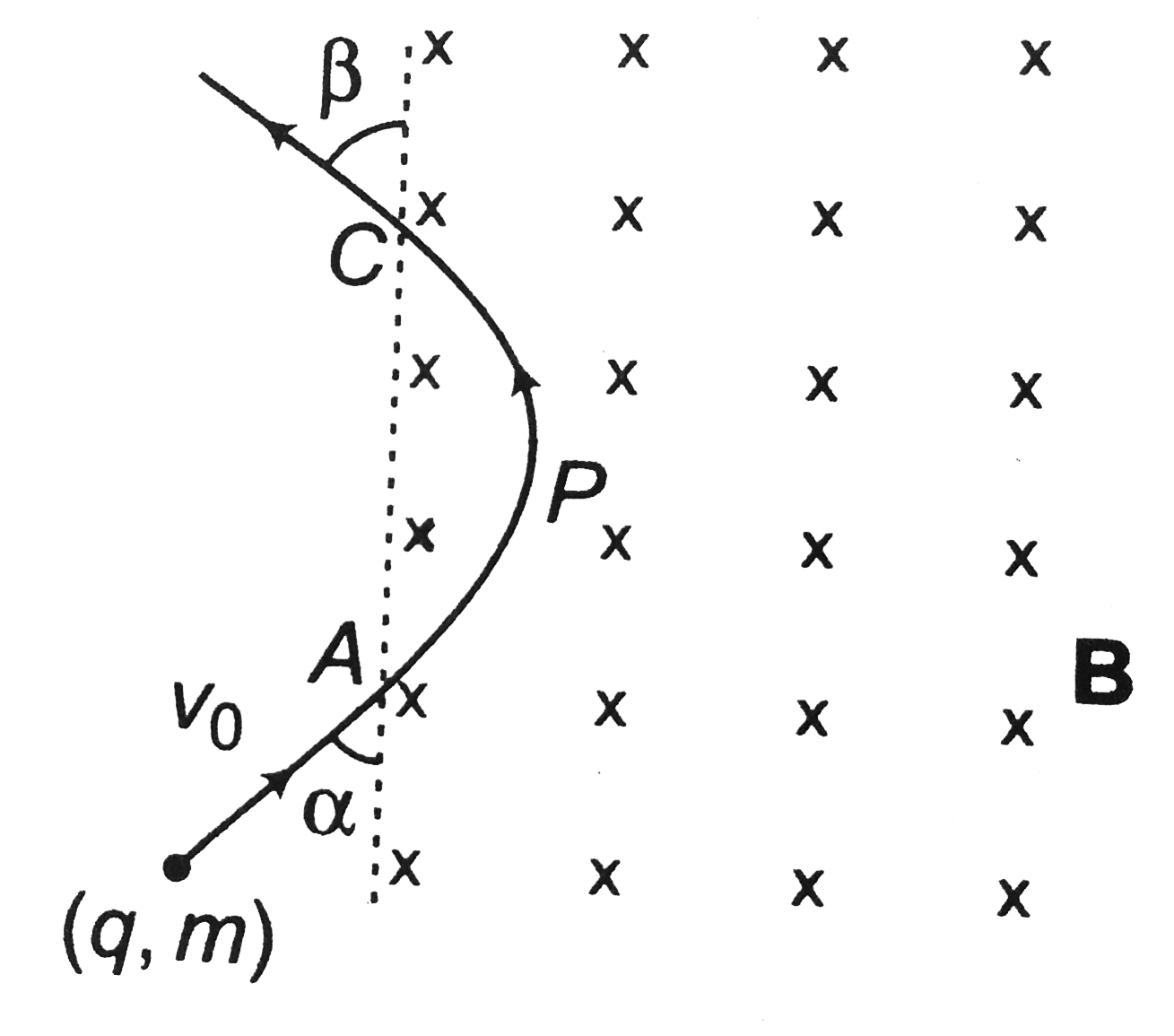
a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find

a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA proton of mass m and charge q enters a region of uniform magnetic field of a magnitude B with a velocity v directed perpendicular to the magnetic field. It moves in a circular path and leaves the magnetic field after completing a quarter of a circle. The time spent by the proton inside the magnetic field is proportional to:
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View Solution