An inductor 20×10−3 a capacitor 100(μ)F and a resistor 50Ω are connected in series across a source of emf V=10sin314t.
If resistance is removed from the circuit and the value of inductance is doubled, the variation of current with time in the new circuit is
0.52cos314t
0.52sin314t
0.52sin(314t+π/3)
none of these.
The correct Answer is:A
To solve the problem step by step, we will analyze the given circuit and apply the relevant formulas for an LCR circuit, followed by the modifications made to the circuit.
Given Data:
- Inductance, L=20×10−3H
- Capacitance, C=100μF=100×10−6F
- Resistance, R=50Ω
- Voltage source, V(t)=10sin(314t)
Step 1: Determine the Angular Frequency
The angular frequency ω can be directly obtained from the voltage source:
ω=314rad/s
Step 2: Calculate the Impedance of the Original Circuit
The impedance Z of an LCR circuit is given by:
Z=√R2+(XL−XC)2
Where:
- XL=ωL=314×(20×10−3)=6.28Ω
- XC=1ωC=1314×(100×10−6)≈31.84Ω
Now substituting the values:
Z=√502+(6.28−31.84)2
Calculating Z:
Z=√2500+(−25.56)2=√2500+653.6336≈√3153.6336≈56.14Ω
Step 3: Calculate the RMS Voltage
The RMS voltage Vrms is given by:
Vrms=V0√2=10√2≈7.07V
Step 4: Calculate the RMS Current
Using Ohm's law for AC circuits:
Irms=VrmsZ=7.0756.14≈0.126A
Step 5: Remove Resistance and Double Inductance
When the resistance is removed, R=0, and the new inductance L′=2L=40×10−3H.
Step 6: Calculate New Reactance Values
Calculate the new inductive reactance:
X′L=ωL′=314×(40×10−3)=12.56Ω
The capacitive reactance remains the same:
XC=31.84Ω
Step 7: Calculate New Impedance
The new impedance Z′ is:
Z′=√02+(XC−X′L)2=|XC−X′L|=|31.84−12.56|=19.28Ω
Step 8: Calculate New Current Amplitude
The new current amplitude I0 is given by:
I0=V0Z′=1019.28≈0.518A
Step 9: Determine Phase Angle
Since XC>X′L, the circuit behaves as capacitive, leading to a phase angle:
ϕ=tan−1(XC−X′LR)=tan−1(31.84−12.560)=π2
Step 10: Write the Current Equation
The instantaneous current can be expressed as:
I(t)=I0sin(ωt+ϕ)=0.518sin(314t+π2)
This can be simplified to:
I(t)=0.518cos(314t)
Final Answer:
The variation of current with time in the new circuit is:
I(t)=0.518cos(314t)
- Inductance, L=20×10−3H
- Capacitance, C=100μF=100×10−6F
- Resistance, R=50Ω
- Voltage source, V(t)=10sin(314t)
The angular frequency ω can be directly obtained from the voltage source:
ω=314rad/s
The impedance Z of an LCR circuit is given by:
Z=√R2+(XL−XC)2
Where:
- XL=ωL=314×(20×10−3)=6.28Ω
- XC=1ωC=1314×(100×10−6)≈31.84Ω
Z=√502+(6.28−31.84)2
Calculating Z:
Z=√2500+(−25.56)2=√2500+653.6336≈√3153.6336≈56.14Ω
The RMS voltage Vrms is given by:
Vrms=V0√2=10√2≈7.07V
Using Ohm's law for AC circuits:
Irms=VrmsZ=7.0756.14≈0.126A
When the resistance is removed, R=0, and the new inductance L′=2L=40×10−3H.
Calculate the new inductive reactance:
X′L=ωL′=314×(40×10−3)=12.56Ω
The capacitive reactance remains the same:
XC=31.84Ω
The new impedance Z′ is:
Z′=√02+(XC−X′L)2=|XC−X′L|=|31.84−12.56|=19.28Ω
The new current amplitude I0 is given by:
I0=V0Z′=1019.28≈0.518A
Since XC>X′L, the circuit behaves as capacitive, leading to a phase angle:
ϕ=tan−1(XC−X′LR)=tan−1(31.84−12.560)=π2
The instantaneous current can be expressed as:
I(t)=I0sin(ωt+ϕ)=0.518sin(314t+π2)
This can be simplified to:
I(t)=0.518cos(314t)
The variation of current with time in the new circuit is:
I(t)=0.518cos(314t)
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Integer
4 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Archives Subjective
1 Video
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
An inductor 20×10−3 a capacitor 100(μ)F and a resistor 50Ω are connected in series across a source of emf V=10sin314t.
Then the energy dissipated in the circuit in 20 mim is
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View Solution
Knowledge Check
An inductor 200 mH, capacitor 500μF and resistor 10Ω are connected in series with a 100 V variable frequency ac source. What is the frequency at which the power factor of the circuit is unity?
A10.22HzB12.4HzC19.2HzD15.9Hz
An inductor 20mH, a capacitor 50μF and a resistor 40Ωare connected in series across of emf V=10sin340t. The power loss in A.C. circuit is
View SolutionAn inductor 2/π Henry, a capacitor 100/TμF and a resistor 75Ω are connected in series across a source of emf V=10sin100πt. Here t is in second. (a) find the impedance of the circuit. (b) find the energy dissipated in the circuit in 20 minutes.
View SolutionAn inductance L , a capacitor of 20μF and a resistor of 10Ω are connected in series with an AC source of frequency 50 Hz . If the current is in phase with the voltage, then the inductance of the inductor is
View SolutionA 25(μ)F capacitor, a 0.1 H inductor and a 25Ω resistor are connected in series with an ac source of emf E=310sin314t. Find
(a) the frequency of the emf
(b) the impedance of the circuit
(c) the current in the circuit.
(d) the phase angle
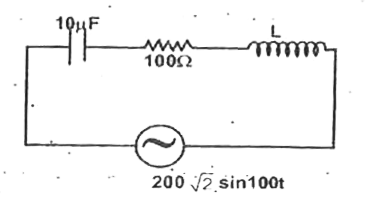
View SolutionA 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
View SolutionA resistance and inductance are connected in series across a voltage,
V=283sin314t
The current is found to be 4sin(314t−π/4). Find the value of the inductance and resistance.
View SolutionA resistance and inductance are connected in series across a voltage,
V=283sin314t
The current is found to be 4sin(314t−π/4). Find the value of the inductance and resistance.
View Solution