A particle is released from the origin with a velocity vˆe(i). The electric field in the region is Eˆe(i) and magnetic field is Bˆk. Then
If v=0andE=0 then particle will execute a circular path.
If v=0,E≠0 then particle is positively charged then it executes clockwise
If v=0 and E≠0 then the particle will execute a cycloidal motion in the x-y plane.
If v>0 and E≠0 and the particle is positievely charged and B>0 then the particle wil excute anticlockwise anticlock wise circle as seen from +z direction.
The correct Answer is:C, D
if v=0,E=0 then no force will act on particle, hence partcle remains at rest
(b) here v=0,E≠0, due to E the particle will gain velocity in x direction. Due to this velocity it will experience force due to magnetic field along negative y axis. As a result of it, the particle will move in curved path that will not be a circle.
(c) If v=0,E≠0, then particle will execute cycloidal motion.
(d) If E=0, then path will be circular.
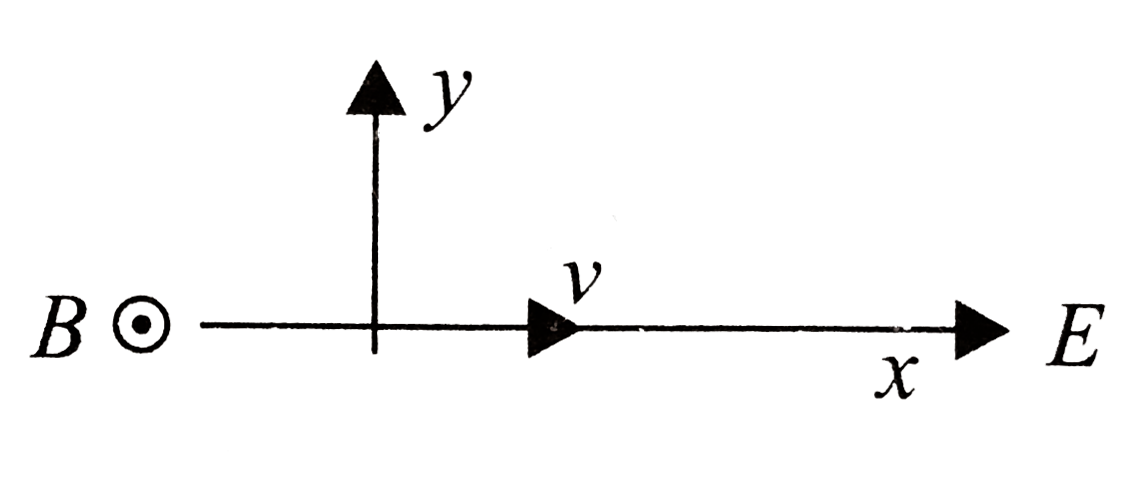
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
A particle of charge q and mass m released from origin with velocity →v=v0ˆi into a region of uniform electric and magnetic fields parallel to y-axis. i.e., →E=E0ˆjand→B=B0ˆj. Find out the position of the particle as a functions of time
Strategy : Here →E∣∣→B
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
ay=Fym=Fem=qE0m
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
→v(t)=vxˆi+vyˆj+vzˆk
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are given by
→B=−B0→Jand→E−E0→K.
Find the speed of the particle as a function of its z-coordinate.
View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionA particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionIf a charged particle at rest experiences no electromagnetic force, then electric field in that region
View SolutionIf a charged particle goes unaccelerated in a region containing electric and magnetic fields,
View SolutionIf a charged particle goes unaccelerated in a region containing electric and magnetic fields,
View SolutionSTATEMENT -1 : When a charged particle is released from a rest in a region of electric field ,its path will represent the electric field lines in the region.
and
STATEMENT-2 : The force experienced by the charged particle will be along a tangent drawn to the electric fieldline at a point.
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View Solution
