A source of sound emits 200πW power which is uniformly distributed over a sphere of radius 10 m. What is the loudness of sound on the surface of the sphere?
70 dB
107 dB
80 dB
117 dB
The correct Answer is:D
To find the loudness of sound on the surface of a sphere with a given power, we can follow these steps:
Step 1: Understand the given data
We have a sound source emitting a power P=200π watts, and the sound is uniformly distributed over a sphere of radius R=10 meters.
Step 2: Calculate the area of the sphere
The area A of a sphere is given by the formula:
A=4πR2
Substituting the value of R:
A=4π(10)2=4π×100=400π m2
Step 3: Calculate the intensity I
Intensity I is defined as power per unit area:
I=PA
Substituting the values of P and A:
I=200π400π=200400=0.5 W/m2
Step 4: Use the formula for loudness
The loudness L in decibels is given by:
L=10log10(II0)
where I0=10−12 W/m2 is the reference intensity.
Step 5: Substitute the values into the loudness formula
Substituting I=0.5 W/m² and I0=10−12 W/m²:
L=10log10(0.510−12)
This simplifies to:
L=10log10(0.5×1012)=10log10(5×1011)=10(log105+11)
Step 6: Calculate log105
Using a calculator or logarithm table, we find:
log105≈0.699
Thus:
L≈10(0.699+11)=10×11.699=116.99 dB
Step 7: Round to the nearest whole number
Rounding 116.99 gives us:
L≈117 dB
Conclusion
The loudness of sound on the surface of the sphere is approximately 117 decibels.
We have a sound source emitting a power P=200π watts, and the sound is uniformly distributed over a sphere of radius R=10 meters.
The area A of a sphere is given by the formula:
A=4πR2
Substituting the value of R:
A=4π(10)2=4π×100=400π m2
Intensity I is defined as power per unit area:
I=PA
Substituting the values of P and A:
I=200π400π=200400=0.5 W/m2
The loudness L in decibels is given by:
L=10log10(II0)
where I0=10−12 W/m2 is the reference intensity.
Substituting I=0.5 W/m² and I0=10−12 W/m²:
L=10log10(0.510−12)
This simplifies to:
L=10log10(0.5×1012)=10log10(5×1011)=10(log105+11)
Using a calculator or logarithm table, we find:
log105≈0.699
Thus:
L≈10(0.699+11)=10×11.699=116.99 dB
Rounding 116.99 gives us:
L≈117 dB
The loudness of sound on the surface of the sphere is approximately 117 decibels.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct
44 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A dog while barking delivers about 1 mW of power. If this power is uniformly distributed over a hemispherical area, what is the sound level at a distance of 5 m? What would the sound level be if instead of 1 dog, 5 dogs start barking at the same time each delivering 1 mW of power
View SolutionA ring of radius 'R' having change 'q' uniformly distributed over it passes through a sphere lies at circumference of ring the centre of ring lies at surface of sphere.Then flux linked with sphere is
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be

View SolutionWhat is the level of loudness of a sound of intensity 10−12W/m2 ?
View SolutionSurface charge density of a sphere of a radius 10 cm is 8.85×10−8c/m2. Potential at the centre of the sphere is
View SolutionA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.

View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View SolutionA charger Q is distributed uniformly on a ring of radius of r. A sphere of equal radius r is constructed with its centre a t the periphery of the ring. The flux of the electric field through the surface of the sphere is Qnε0 , The value of n is
View SolutionA Charge Q is distributed uniformly on a ring of radius r. A sphere of equal r is constructed with its centre at the periphery of the ring (figure 30.12) Find the flux of the electric field through the surface of the sphere.
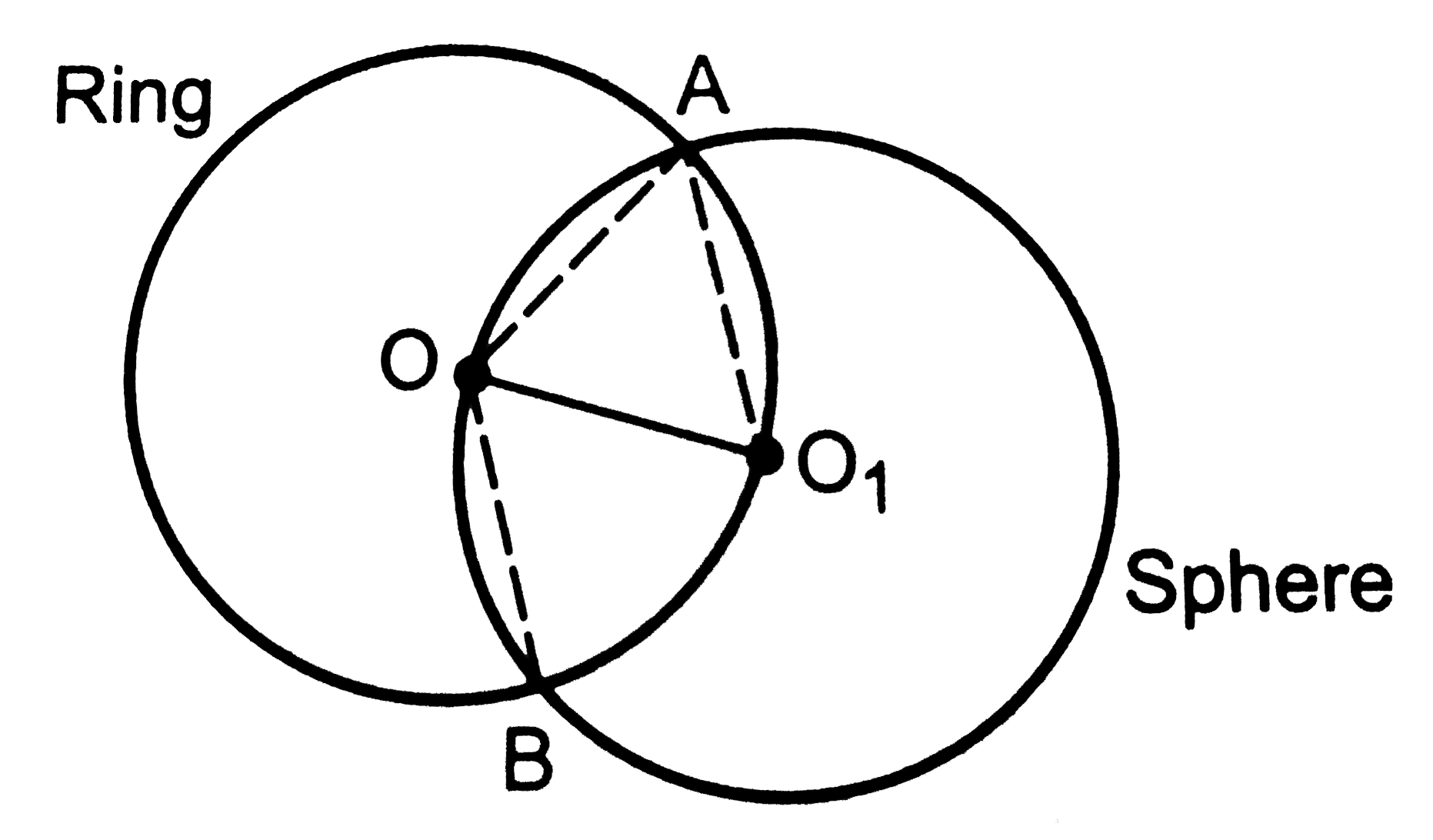
View SolutionA source emits 31.4 W of radiant flux distributed uniformly in all directions. The luminous efficiency is 60 lumen watt. What is the luminous intensity of the source ?
View Solution
