A uniform copper bar 100 cm long is insulated on side, and has its ends exposed to ice and steam respectively. If there is a layer of water 0.1 mm thick at each end, calculate the temperature gradient in the bar. KCu=1.04 and Kwater=0.0014 in CGS units.
To solve the problem, we will calculate the temperature gradient in the copper bar by considering the thermal resistances of the water layers and the copper bar itself.
1. Identify the Given Data:
- Length of the copper bar, L=100cm
- Thickness of water layer at each end, d=0.1mm=0.01cm
- Temperature at one end (steam), T1=100°C
- Temperature at the other end (ice), T2=0°C
- Thermal conductivity of copper, KCu=1.04cal/cm⋅s⋅°C
- Thermal conductivity of water, Kwater=0.0014cal/cm⋅s⋅°C
2. Calculate the Thermal Resistance of the Water Layers:
- The thermal resistance Rwater for one water layer is given by:
Rwater=dKwater⋅A
- Since there are two water layers, the total thermal resistance for the water layers is:
Rtotal_water=2⋅Rwater=2⋅dKwater⋅A
3. Calculate the Thermal Resistance of the Copper Bar:
- The thermal resistance RCu of the copper bar is given by:
RCu=LKCu⋅A
4. Set Up the Heat Transfer Equation:
- The heat transfer through the entire system can be expressed as:
Q=T1−T2Rtotal_water+RCu
- Substituting the expressions for Rtotal_water and RCu:
Q=1002⋅0.010.0014⋅A+1001.04⋅A
5. Simplify the Equation:
- This simplifies to:
Q=100⋅A0.020.0014+1001.04
6. Calculate the Total Resistance:
- Calculate 0.020.0014 and 1001.04:
0.020.0014≈14.2857and1001.04≈96.1538
- Therefore, the total resistance is:
Rtotal≈14.2857+96.1538≈110.4395
7. Substitute Back to Find Q:
- Now substituting back:
Q=100⋅A110.4395
8. Relate Q to Temperature Gradient:
- The heat transfer through the copper bar can also be expressed as:
Q=KCu⋅A⋅dTdx
- Setting the two expressions for Q equal gives:
100⋅A110.4395=1.04⋅A⋅dTdx
9. Solve for the Temperature Gradient:
- Cancel A from both sides:
100110.4395=1.04⋅dTdx
- Rearranging gives:
dTdx=1001.04⋅110.4395
- Calculate dTdx:
dTdx≈0.87°C/cm
Final Answer:
The temperature gradient in the copper bar is approximately 0.87°C/cm.
- Length of the copper bar, L=100cm
- Thickness of water layer at each end, d=0.1mm=0.01cm
- Temperature at one end (steam), T1=100°C
- Temperature at the other end (ice), T2=0°C
- Thermal conductivity of copper, KCu=1.04cal/cm⋅s⋅°C
- Thermal conductivity of water, Kwater=0.0014cal/cm⋅s⋅°C
- The thermal resistance Rwater for one water layer is given by:
Rwater=dKwater⋅A
- Since there are two water layers, the total thermal resistance for the water layers is:
Rtotal_water=2⋅Rwater=2⋅dKwater⋅A
- The thermal resistance RCu of the copper bar is given by:
RCu=LKCu⋅A
- The heat transfer through the entire system can be expressed as:
Q=T1−T2Rtotal_water+RCu
- Substituting the expressions for Rtotal_water and RCu:
Q=1002⋅0.010.0014⋅A+1001.04⋅A
- This simplifies to:
Q=100⋅A0.020.0014+1001.04
- Calculate 0.020.0014 and 1001.04:
0.020.0014≈14.2857and1001.04≈96.1538
- Therefore, the total resistance is:
Rtotal≈14.2857+96.1538≈110.4395
- Now substituting back:
Q=100⋅A110.4395
- The heat transfer through the copper bar can also be expressed as:
Q=KCu⋅A⋅dTdx
- Setting the two expressions for Q equal gives:
100⋅A110.4395=1.04⋅A⋅dTdx
- Cancel A from both sides:
100110.4395=1.04⋅dTdx
- Rearranging gives:
dTdx=1001.04⋅110.4395
- Calculate dTdx:
dTdx≈0.87°C/cm
The temperature gradient in the copper bar is approximately 0.87°C/cm.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Single Correct
148 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A uniform copper rod 50 cm long is insulated on the sides, and has its ends exposedto ice and steam,respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionA copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at 100∘C and the other at 0∘C. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient dTdx and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 W/m−K.
View SolutionA copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at 100∘C and the other at 0∘C. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient dTdx and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 W/m.K.
View SolutionA plate of area 10cm2 is to be electroplated with copper (density9000kgm−3 to a thickness of 10 micrometres on both sides, using a cell of 12V. Calculate the energy spend by the cell in the process of deposition. If this energy is used to heat 100g of water, calculate the rise in the temperature of the water. ECE of copper =3×10−7kgC−1 and specific heat capacity of water =4200Jkg−1K−1.
View SolutionA steel bar 10.0 cm long is welded end to end to a copper bar 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100∘C by placing it in contact with steam and free end of the copper bar is maintained at 0∘C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel =50.2Wm−1K−1.thermal conductivity of copper =385Wm−1K−1.
View SolutionIn an experiment to determine the thermal conductivity of copper with Searle's apparatus, 100 gm of water flowed in 4.2 minutes past the cold end of the copper bar, its initial and final temperatures being 25°C and 52°C respectively. If the temperature difference between two points in the bar 10 cm apart is 23°C and the area of cross-section of the bar is 5 cm2, calculate the coefficient of thermal conductivity of copper. Specific heat capacity of water 4,200J kg−1K−1
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
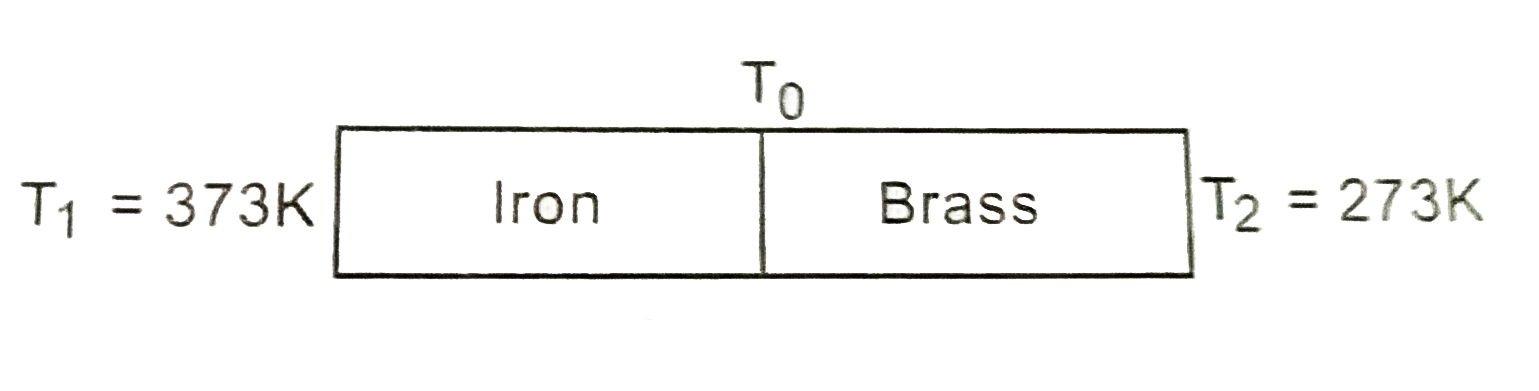 .
.
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View Solution
