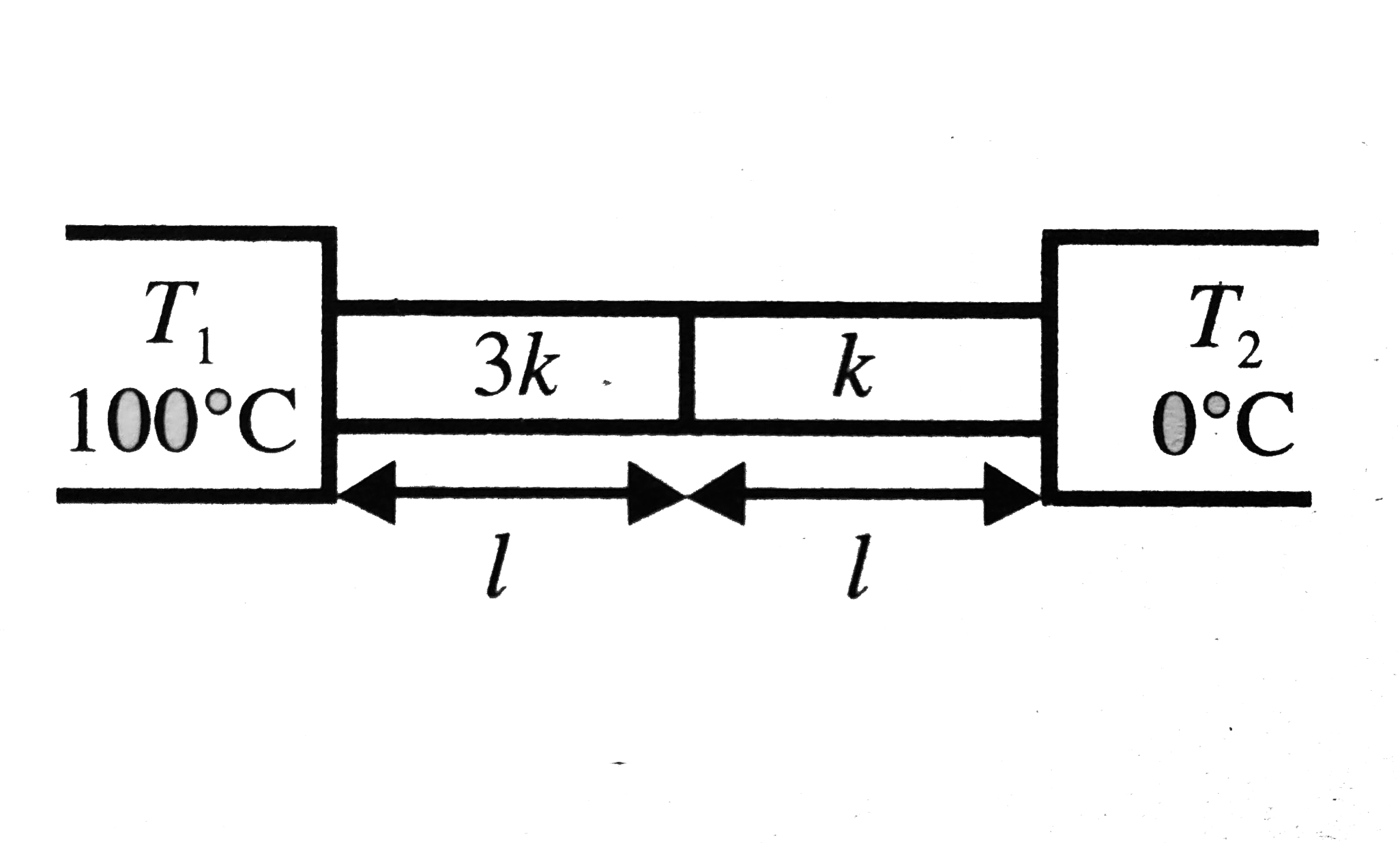
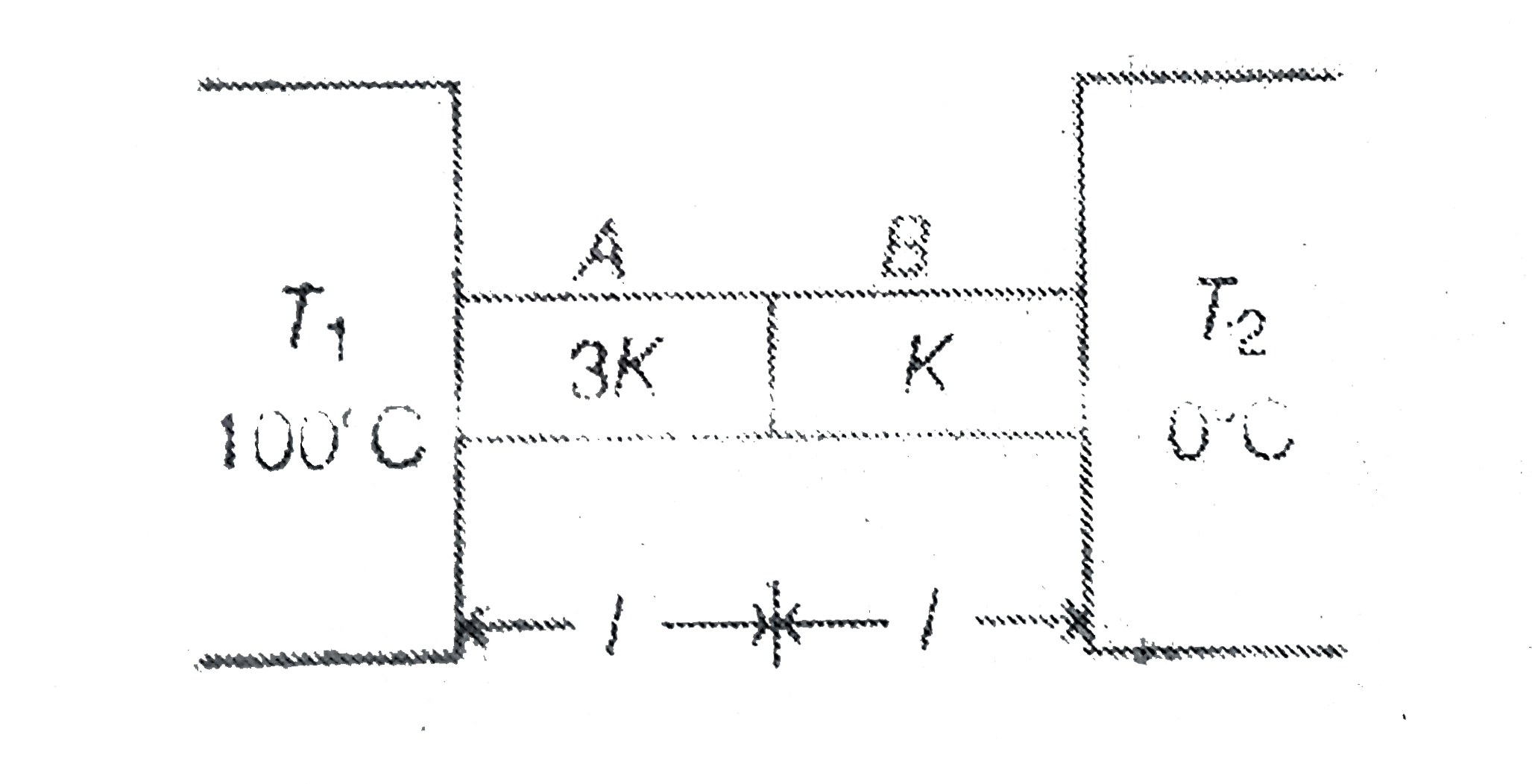
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
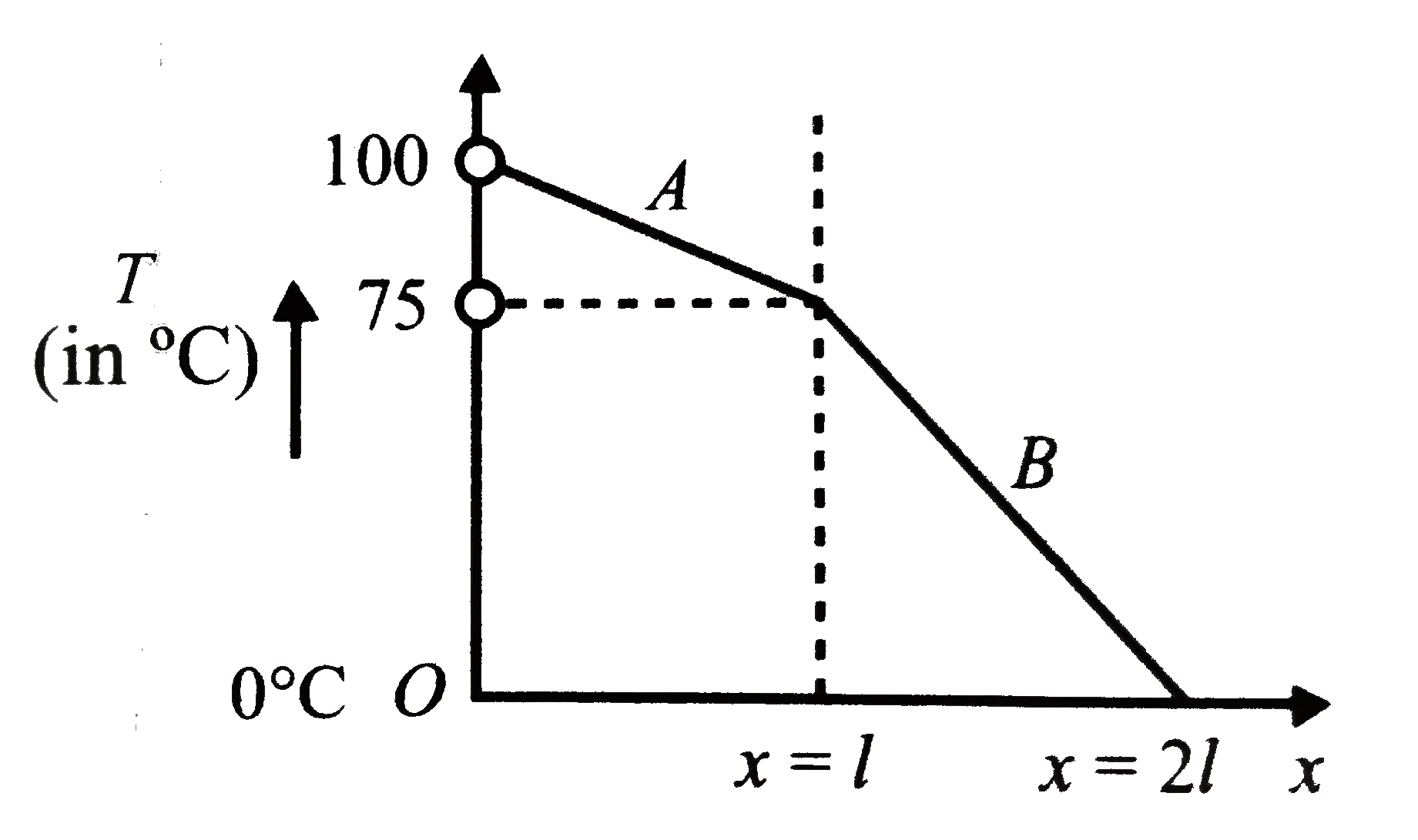
iv. plot the variation of temperature along the length of the rod.
i. Thermal resistance is defined as R=l/kA
For rod A RA=lkAA=l3kA
For rod B RB=lkBA=lkA
ii. Using electrical analogy, the given problem may be modified as The equivalent resistance is R=RA+RB=43lkA
The heat current is given by
I=T1−T2R=100−043lkA=73(kAl)
iii. The temperature of the junction is given by
T=T1−IRA=100−75kAl(l3kA)=75∘C
iv. The variation of temperature along the length of the conductor is shown in Fig.

Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Single Correct
148 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
The thermal conductivity of a rod depends on
View SolutionThe thermal conductivity of a rod depends on
View SolutionThe thermal conductivity of a rod depends on
View Solution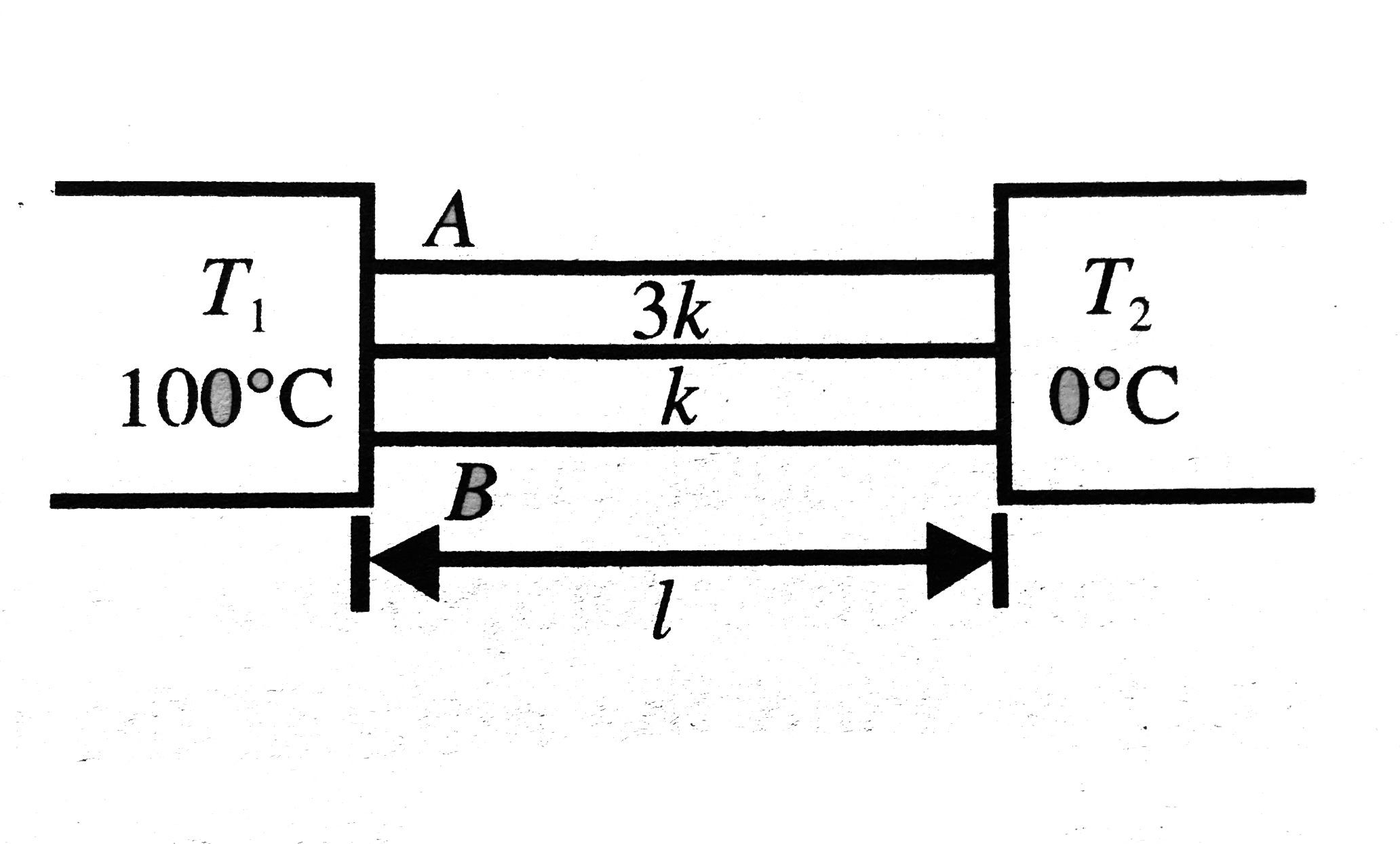
Two conductors A and B are connected in parallel as shown in Fig.
i. Determine the equivalent thermal resistance.
ii. Determine the heat current in each rod.
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
The ratio of the thermal resistance of the rods is
View SolutionThe ratio of the thermal conductivities of two different materials is 1:2. The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionTwo rods A and B of same area of cross-section are joined together end to end The free end of the rod A is kept in melting ice at 300 K and free end of B rod at 400 K. The rods are of the same length. The conductivity of A is 3 times that of B. Calculate the temperature of the junction of the rods.
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.

If TA and TB are the temperature drops across the rod A and B, then
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
If GA and GB are the temperature gradients across the rod A and B, then
View Solution