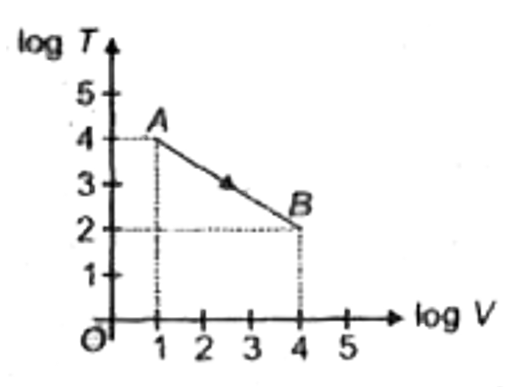
Figure shows the adiabatic curve for n moles of an ideal gas, the bulk modulus for the gas corresponding to the point P will be

5nRT03V0
nR(2+T0V0)
nR(1+T0V0)
2nRT0V0
The correct Answer is:D
d. For adiabatic process :
Bulk modulus : B=γP
for point p:P=nRTV=nR3T03V0=nRT0V0
⇒B=γnRT0V0
Now TVγ−1= constant
⇒(γ−1)TdV+VdT=0
⇒dVdT=−V(γ−1)T
for point P→
−3V03T0=−(3V0)(γ−1)(eT0)0
⇒γ=2
so from Eq. (i) B=2nRT0V0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects29videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning6videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective22videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
In an adiabatic expansion of an ideal gas -
A(a) W=−ΔUB(b) W=ΔUC(c) ΔU=0D(d) W=0
For n moles of ideal gas, the equation of state may be written as
View SolutionFor adiabatic process of an ideal gas the value of dPP is equals to
View SolutionDuring an adiabatic reversibly expansion of an ideal gas
View SolutionThe bulk modulus of an ideal gas at constant temperature
View SolutionAdiabatic expansion of an ideal gas is accompanied by
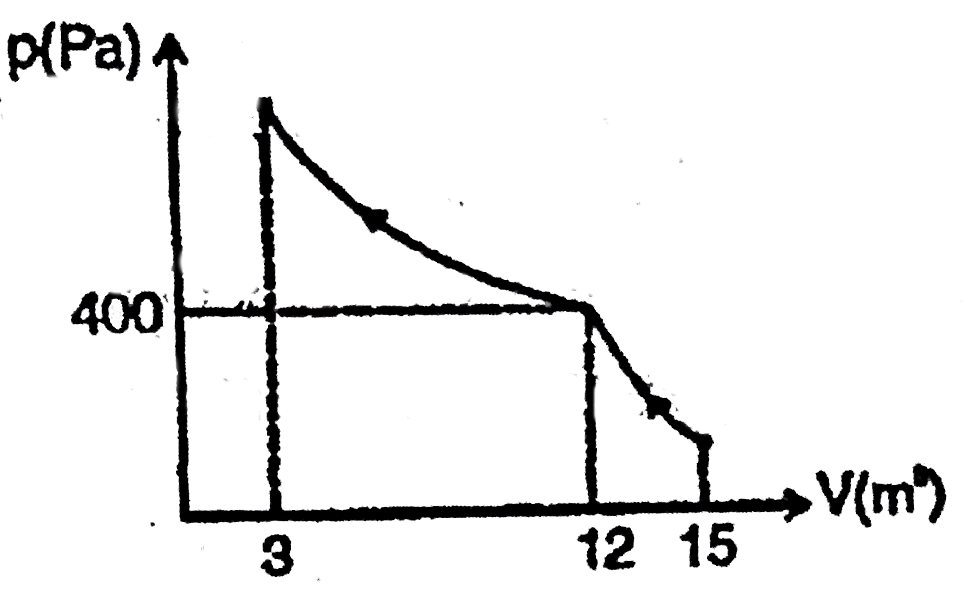
View SolutionCurve in the figure shows an adiabatic compression of an ideal gas from 15m3 to 12m3, followed by an isothermal compression to a final volume of 3.0m3. There are 2.0 moles of the gas. Total heat supplied to the gas is equal to: (ln2= 0.693)
 View Solution
View SolutionFor a reversible adiabatic expansion of an ideal gas dp/p is equal to
View Solution


_S01_085_Q01.png)