A particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
The kinetic energy of the partical when it is mean position. It is also its total energy as the potential energy is zero here .
E=12mv2=12(0.50kg)(10m/s)2=25J
As the maximum displacement x=A, the speed is zero and hence the kinetic energy here is 1/2kA2. At this position it will also its total energy . Hence
12kA2=25J (i)
The force on the partical is gives by F=−(50N/m)x
Thus, the spring constant is k=50N/m
Equation (i) gives
12(50N/m)A2=25J⇒A=1m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example15videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A particle of mass 0.1 kg executes SHM under a for F=(−10x) N. Speed of particle at mean position 6m/s. Then amplitude of oscillations is
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle executes simple harmonic motion of period 16s. Two seconds later after it passes through the center of oscillation its velocity is found to be 2m/s. Find the amplitude.
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA partical of mass 0.2kg executes simple harmonic motion along a path of length 0.2m at the rate of 600oscillations per minute. Assum at t=0. The partical start SHM in positive direction. Find the kinetic potential energies in joules when the displacement is x=A/2 where, A stands for the amplitude.
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
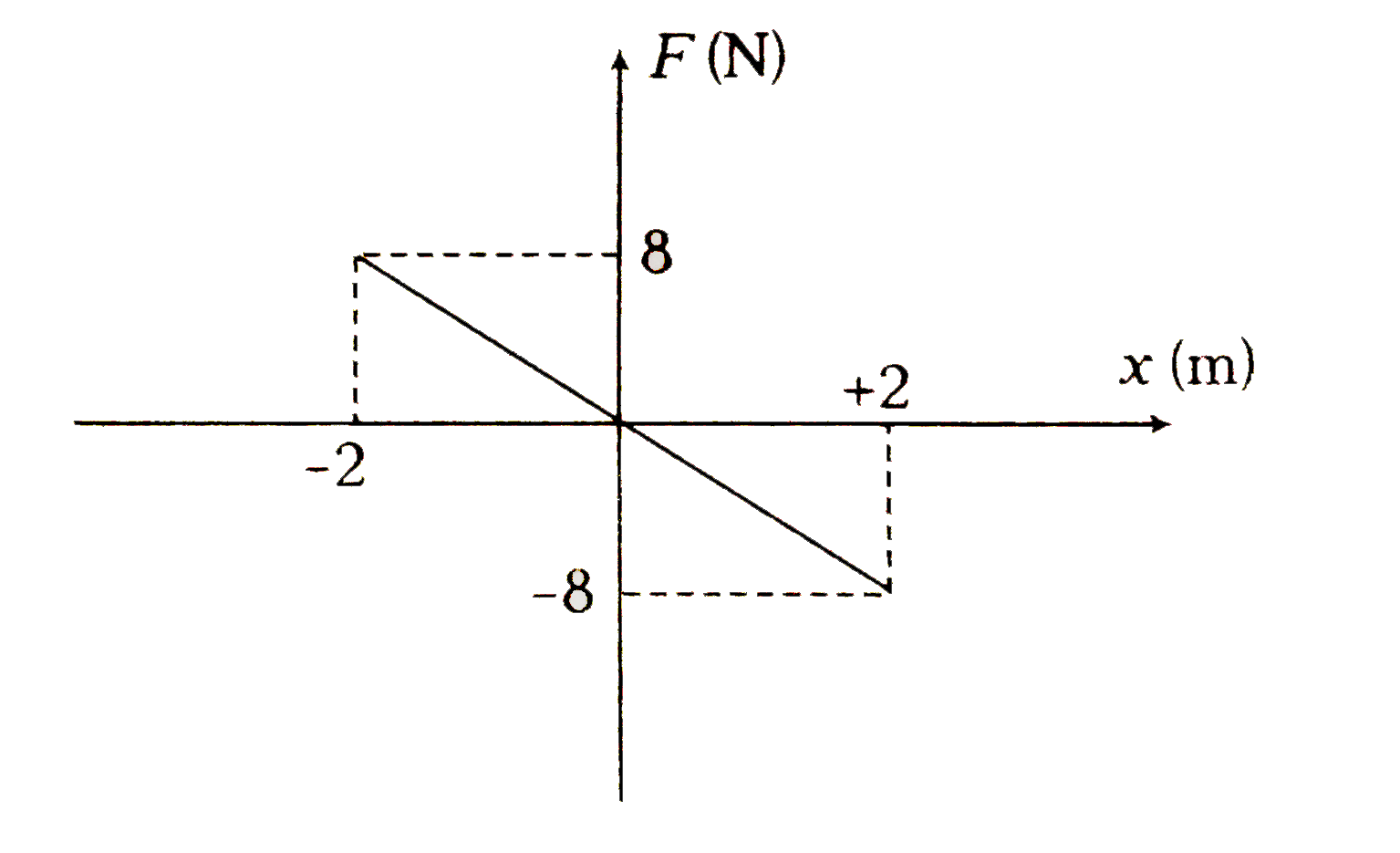 View Solution
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
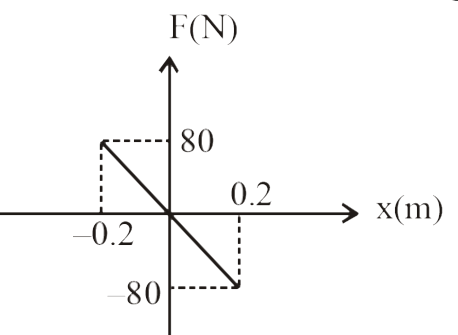 View Solution
View SolutionA particle executing simple harmonic motion of amplitude 5cm has maximum speed of 31.4cm/s. The frequency of its oscillation is
View Solution

