A body of mass 100 g attached to a spring executed SHM of period 2 s and amplitude 10 cm. How long a time is required for it to move from a point 5 cm below its equilibrium position to a point 5 cm above it, when it makes simple harmonic vertical oscillation (take g=10ms2)?
0.6 s
13s
1.5s
2.2s
The correct Answer is:B
To solve the problem, we need to determine the time taken for a body executing simple harmonic motion (SHM) to move from a point 5 cm below its equilibrium position to a point 5 cm above it. Here’s a step-by-step solution:
Step 1: Understand the parameters of the SHM
- Mass of the body, m=100g=0.1kg
- Period, T=2s
- Amplitude, A=10cm=0.1m
Step 2: Determine the angular frequency ω
The angular frequency ω can be calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π2=πrad/s
Step 3: Set up the displacement equation
The displacement x in SHM can be expressed as:
x(t)=Acos(ωt)
For our case:
x(t)=0.1cos(πt)
Step 4: Calculate the time t1 to reach 5 cm below the equilibrium position
At 5 cm below the equilibrium position:
x=−5cm=−0.05m
Setting up the equation:
−0.05=0.1cos(πt1)
This simplifies to:
−0.5=cos(πt1)
Taking the inverse cosine:
πt1=cos−1(−0.5)
The angle corresponding to cos−1(−0.5) is 2π3 (in the second quadrant). Therefore:
t1=23s
Step 5: Calculate the time t2 to reach 5 cm above the equilibrium position
At 5 cm above the equilibrium position:
x=5cm=0.05m
Setting up the equation:
0.05=0.1cos(πt2)
This simplifies to:
0.5=cos(πt2)
Taking the inverse cosine:
πt2=cos−1(0.5)
The angle corresponding to cos−1(0.5) is π3 (in the first quadrant). Therefore:
t2=13s
Step 6: Calculate the time taken to move from point P to point Q
The total time taken to move from point P (5 cm below) to point Q (5 cm above) is:
Δt=t2−t1=13−23=13s
Final Answer
The time required for the body to move from a point 5 cm below its equilibrium position to a point 5 cm above it is 13 seconds.
---
- Mass of the body, m=100g=0.1kg
- Period, T=2s
- Amplitude, A=10cm=0.1m
The angular frequency ω can be calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π2=πrad/s
The displacement x in SHM can be expressed as:
x(t)=Acos(ωt)
For our case:
x(t)=0.1cos(πt)
At 5 cm below the equilibrium position:
x=−5cm=−0.05m
Setting up the equation:
−0.05=0.1cos(πt1)
This simplifies to:
−0.5=cos(πt1)
Taking the inverse cosine:
πt1=cos−1(−0.5)
The angle corresponding to cos−1(−0.5) is 2π3 (in the second quadrant). Therefore:
t1=23s
At 5 cm above the equilibrium position:
x=5cm=0.05m
Setting up the equation:
0.05=0.1cos(πt2)
This simplifies to:
0.5=cos(πt2)
Taking the inverse cosine:
πt2=cos−1(0.5)
The angle corresponding to cos−1(0.5) is π3 (in the first quadrant). Therefore:
t2=13s
The total time taken to move from point P (5 cm below) to point Q (5 cm above) is:
Δt=t2−t1=13−23=13s
The time required for the body to move from a point 5 cm below its equilibrium position to a point 5 cm above it is 13 seconds.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A particle executes SHM of period 1.2s and amplitude 8cm. Find the time it takes to travel 3cm from the positive extremity of its oscillation. [cos−1(5/8)=0.9rad]
View SolutionA particle executes SHM with amplitude of 20 cm and time period of 12 s. What is the minimum time required for it to move between two points 10 cm on either side of the mean position?
View Solution
Knowledge Check
A particle is executing simple harmonic motion of amplitude 5 cm and period 6 s. How long will it take to move from one end of its path on one side of mean position to a position 2.5 cm on the same side of the mean position ?
A1 sB1.5 sC3 sD3.5 s
A body is in simple harmonic motion with time period T = 0.5 s and amplitude A = 1 cm. Find the average velocity in the interval in which it moves from equilibrium position to half of its amplitude.
View SolutionA particle executes shm with an amplitude of 10 cm and a period of 5 s. Find the velocity and acceleration of the particle of a distance 5 cm from the equilibrium position.
View SolutionA body of mass 0.10kg is attached to vertical massless spring with force constant 4.0×103N/m. The body is displaced 10.0cm from its equilibrium position and released. How much time elapses as the body moves from a point 8.0cm on one side of the equilibrium position to a point 6.0cm on the same side of the equilibrium position ?
View SolutionA particle executing SHM of amplitude 4 cm and T=4s .The time taken by it to move from positive extreme position to half the amplitude is
View Solution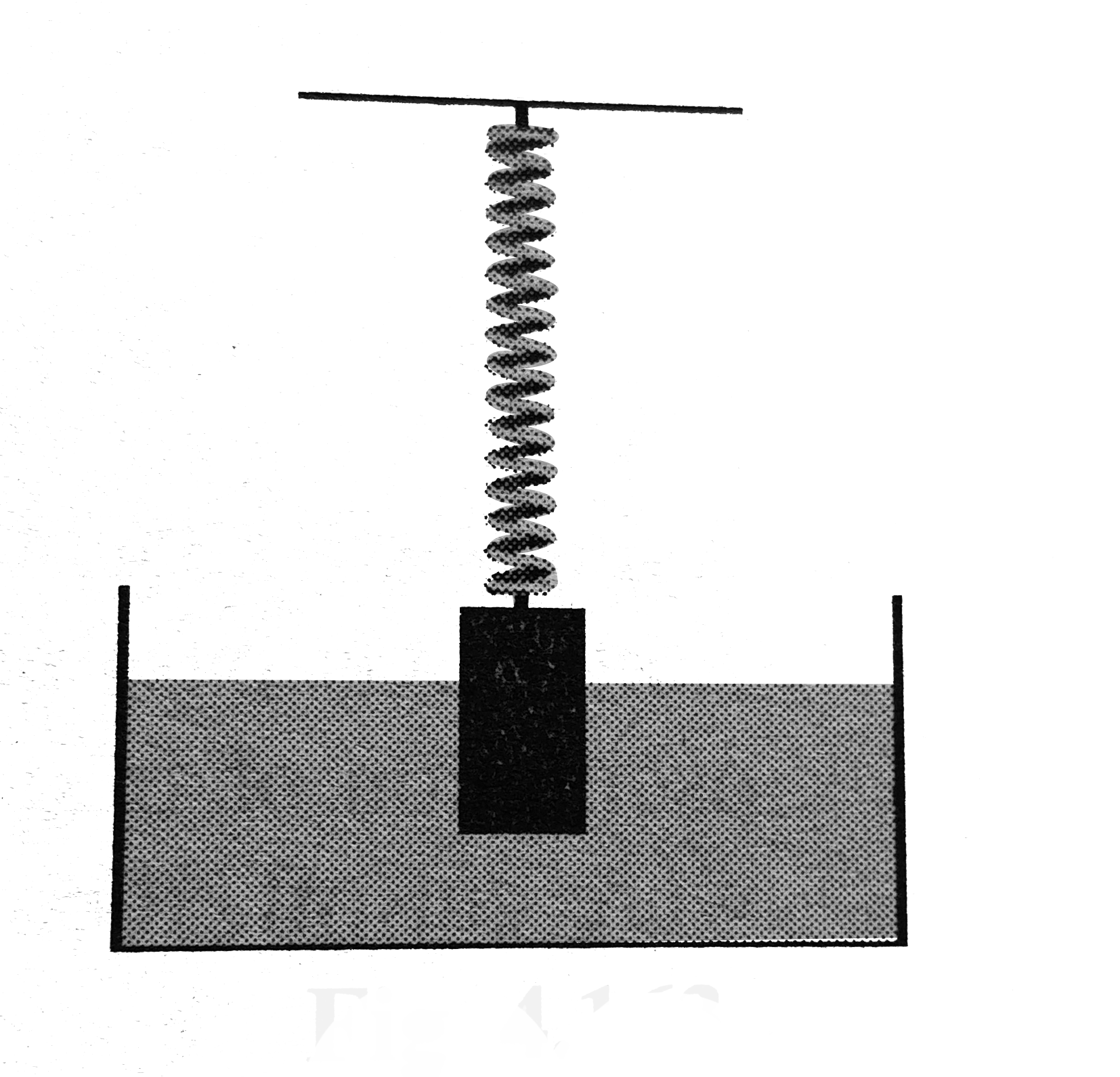
A solid right circular cylinder of weight 10 kg and cross sectional area 100cm2 is suspended by a spring, where k=1kgcm, and hangs partially submerged in water of density 1000kgm3 as shown in Fig. What is its perod when it makes simple harmonic vertical oscillations? (Take g=10ms2)
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View SolutionA particle executes SHM with a time period of 2s and amplitude 10 cm . Find its (i) Displacement (ii) Velocity (iii) Acceleration after 1/6 s, Starting from mean position.
View Solution
