A block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.

The correct Answer is:A
At mean position, acceleration, a=0
⇒N=mg (N = normal reaction)
Below the mean positon, acceleration is upwards (towards the mean position)
∴N−mg=ma or N=m(g+a)
Above the mean position, acceleration is downwards (towards the mean position)
∴mg−N=ma or N=m(g−a)
In this case, N decreases as 'alpha' increases. At the extreme position acceleration is maximum (=ω2A) so N is minimum. When the block leaves contact with the plank N becomes zero.
∴0=m(g−ω2A) or A=gω2
Therfore, the maximum value of amplitude A for not leaving the contact is gω2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 6
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 7
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 4
1 Video
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionIn Fig. A is a large block which executes shm by sliding across a frictionless surface with a frequency n. The block B is at rest on the surface of the block μs The coefficient of static friction between the two is H. Find the maximum amplitude of oscillation of the system so that the block B does not slip.
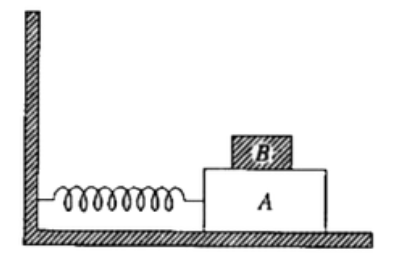
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionFind minimum value of l so that truck can avoid the dead end, without toppling the block kept on it.

View SolutionMaximum amplitude of SHM so block A will not slip on block B, K=100N/m

View SolutionA particle performing SHM with angular frequency ω=5000 radian/second and amplitude A=2 cm and mass of 1 kg. Find the total energy of oscillation.
View SolutionA block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
View SolutionA particle of mass m executing SHM with angular frequency ω0 and amplitude A0, The graph of velocity of the particle with the displacement of the particle from mean position will be(ω0=1)
View SolutionA small block is kept on a platform executing SHM in the horizontal plane, described by x=Asinωt. The time period of SHM is T and the coefficient of friction between the block and the platform is μ. The condition that the block does not slip on the platform at any instant is μ≥xπ2AgT2 then write the value of 'x'

View SolutionA horizontal platform with an object placed on it is executing SHM in the vertical direction. The amplitude of oscillation is 4×10−3m. The least period of these oscillations, so that the object is not detached from the platform is π5x second. Find value of x. Take g=10m/s2
View Solution