
Q. Statement I: Two cubical blocks of same material and of sides a and 2a, respectively are attached rigidley and symmetrically to each other as shown. The system of two blocks is floating in water in such a way that upper surface of bigger blocks is just submerged in the water . If the system of blocks is displaced slightly in vertical directions, then the amplitude of oscillation on either side of equilibrium position would be different. Statement II: The force constant on two sides of equilibrium position in the above described situation is different.
Statement I is true statement II is true, Statement II is a correct explanation for Statement I.
Statement I is true statement II is true, Statement II is NOT a correct explanation for Statement I.
Statement I is true, Statement II is false
Statement I is false, Statement II is true
The correct Answer is:A
Let us assume that density of material of cubes be ρ0 and density of liquid be ρ. Then from equilibrium condition (8a2+a2)ρ0g=(8a2)ρg
⇒9ρ0=8ρ
When the block is displaced down by x, the restoring force is F1=(8a3+a3x)ρg−9a30=ρa2g×x When the block is displaced by x above the mean position, the restoring force is
F2=9a3ρ0g−(8a3−4a2x)ρg=4a2ρgx
As force constant on two sides of equilibrium position are not same, amplitudes of oscillations on the two sides are different.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension33videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer10videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
figure (a) and (b) represent spring- block system. If m is displacement slightly , find the time period of ascillation of the system.
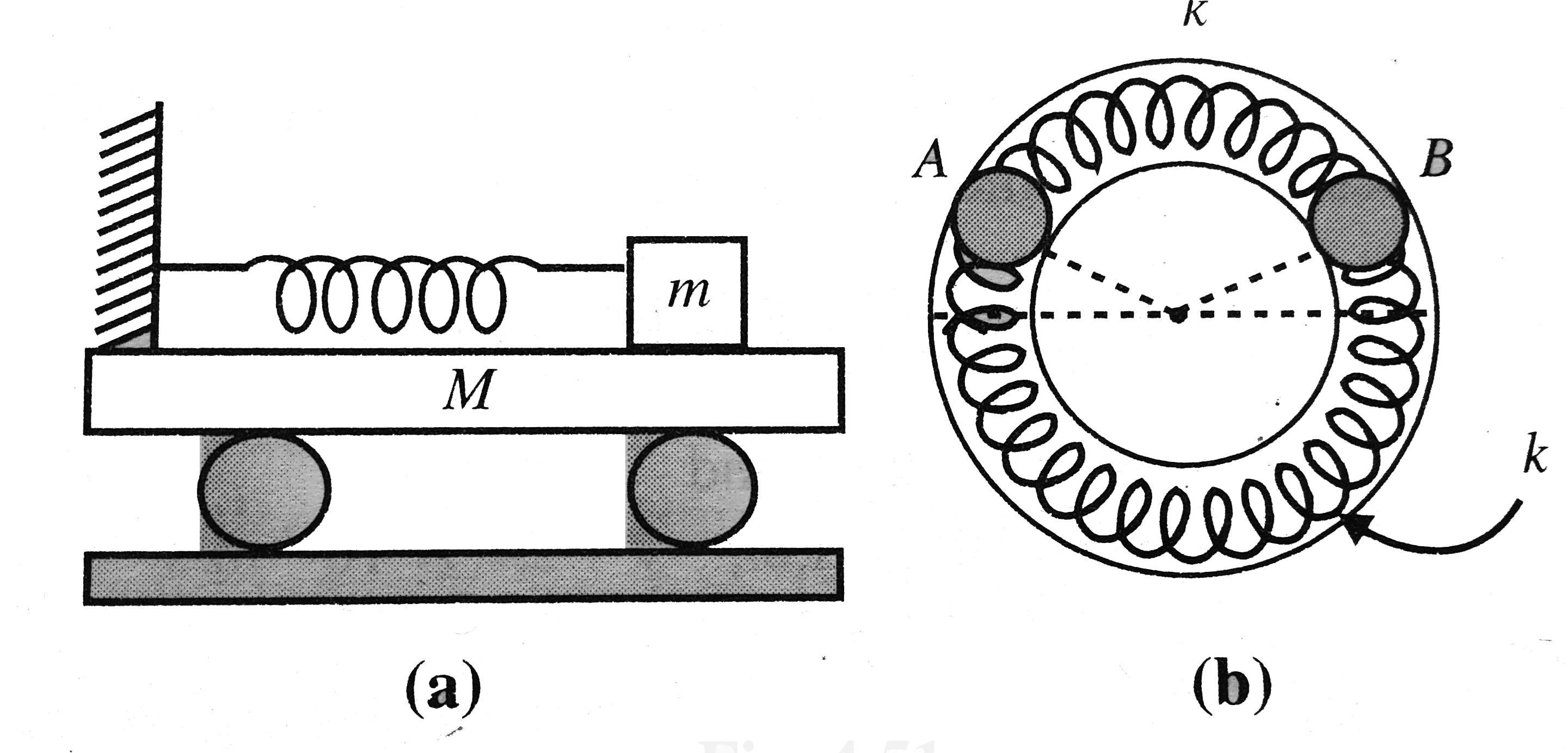 View Solution
View SolutionTwo cubical blocks identical in dimensions float in water in such a way that 1st block floats with half part immersed in water and second block floats with 3/4 of its volume inside the water. The ratio of densities of blocks is
View SolutionA block of mass 1 kg is placed inside a car of mass 5 kg , as shown . The block can slide smoothly along horizontal direction. If block is displaced slightly and released , then time period of osciallation is
 View Solution
View SolutionA wooden block is floating on water kept in a beaker. 40% of the block is above the water surface. Now the beaker is kept inside a lift that starts going upward with acceleration equal to g/2. The block will then
View SolutionA wooden block floats in water with two third of its volume submerged. A. Calculate the density of wood.b. When the same block is placed in oil, three - quarter of its volume in immersed in oil. Calculate the density of oil.
View SolutionA cubical block of density ρ is floating on the surface of water. Out of its height L, fraction x is submerged in water. The vessel is in an elevator accelerating upward with acceleration a. What is the fraction immersed ?
View SolutionA block of wood is floating in water such that 1/2 of it is submerged in water when the same block is floated in alcohol, 1/3rd of it's volume is submerged Now a mixture of water and alcohol is made taking equal volume of both and block is floated in it. What is the % of it's volume that is now submerged?
View SolutionA block of wood is floating in water such that 1/2 of it is submerged in water when the same block is floated in alcohol, 1/3rd of it's volume is submerged Now a mixture of water and alcohol is made taking equal volume of both and block is floated in it. What is the % of it's volume that is now submerged?
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
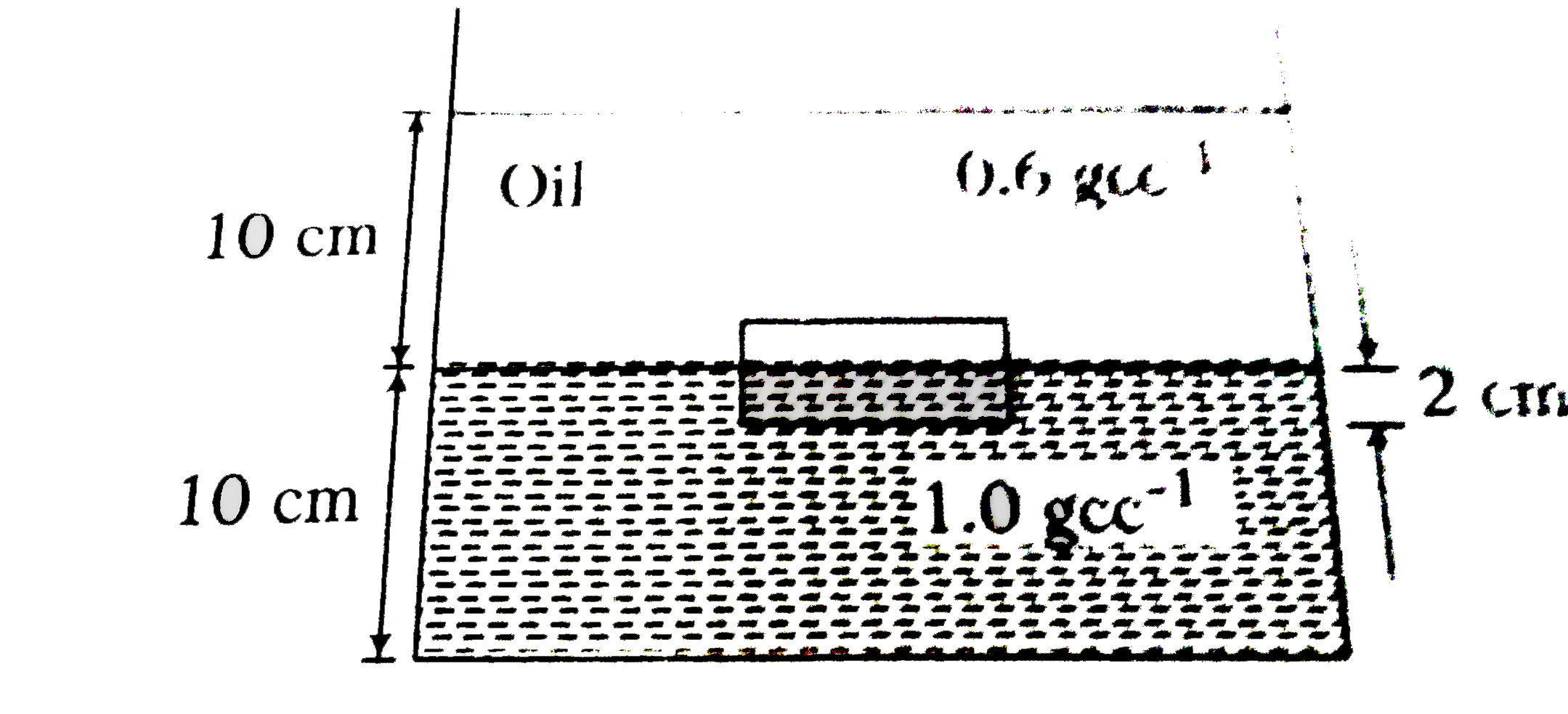 View Solution
View SolutionA system is shown in the figure. The force The time period for small oscillations of the two blocks will be
 View Solution
View Solution

