How long will it take sound waves to travel the distance l between the point A and B if the air temperature between them varies linearly from T1→T2? The velocity of sound propagation in air is equal to va√T where a is a constant.
To solve the problem of how long it will take sound waves to travel the distance L between points A and B, where the air temperature varies linearly from T1 to T2, we can follow these steps:
Step 1: Understand the relationship between temperature and distance
The temperature T varies linearly from T1 to T2 as we move from point A (at x=0) to point B (at x=L). We can express this relationship mathematically as:
T(x)=T1+(T2−T1L)x
This equation represents the temperature as a function of the distance x.
Step 2: Write the velocity of sound as a function of temperature
The velocity v of sound in air is given by:
v=a√T
where a is a constant.
Step 3: Relate distance, velocity, and time
We know that the velocity can also be expressed in terms of distance and time:
v=dxdt
Thus, we can write:
dxdt=a√T
Step 4: Substitute for T in terms of x
From the equation of temperature, we can substitute T into the velocity equation:
dxdt=a√T1+(T2−T1L)x
Step 5: Rearrange and integrate
We can rearrange the equation to separate variables:
dx√T1+(T2−T1L)x=adt
Now, we will integrate both sides. The limits for x will be from 0 to L, and for t from 0 to t.
Step 6: Perform the integration
Integrating the left-hand side requires a substitution. Let:
u=T1+(T2−T1L)x
Then, du=(T2−T1L)dx or dx=LT2−T1du.
Changing the limits accordingly:
- When x=0, u=T1
- When x=L, u=T2
Now, the integral becomes:
∫T2T1LT2−T11√udu=a∫t0dt
Step 7: Solve the integrals
The left-hand side evaluates to:
LT2−T1(2√u)T2T1=LT2−T1(2√T2−2√T1)
The right-hand side evaluates to at.
Setting both sides equal gives:
LT2−T1(2√T2−2√T1)=at
Step 8: Solve for t
Rearranging gives:
t=2La⋅√T2−√T1T2−T1
Final Result
Thus, the time t it takes for sound waves to travel the distance L is:
t=2La⋅√T2−√T1T2−T1
The temperature T varies linearly from T1 to T2 as we move from point A (at x=0) to point B (at x=L). We can express this relationship mathematically as:
T(x)=T1+(T2−T1L)x
This equation represents the temperature as a function of the distance x.
The velocity v of sound in air is given by:
v=a√T
where a is a constant.
We know that the velocity can also be expressed in terms of distance and time:
v=dxdt
Thus, we can write:
dxdt=a√T
From the equation of temperature, we can substitute T into the velocity equation:
dxdt=a√T1+(T2−T1L)x
We can rearrange the equation to separate variables:
dx√T1+(T2−T1L)x=adt
Now, we will integrate both sides. The limits for x will be from 0 to L, and for t from 0 to t.
Integrating the left-hand side requires a substitution. Let:
u=T1+(T2−T1L)x
Then, du=(T2−T1L)dx or dx=LT2−T1du.
- When x=0, u=T1
- When x=L, u=T2
∫T2T1LT2−T11√udu=a∫t0dt
The left-hand side evaluates to:
LT2−T1(2√u)T2T1=LT2−T1(2√T2−2√T1)
The right-hand side evaluates to at.
LT2−T1(2√T2−2√T1)=at
Rearranging gives:
t=2La⋅√T2−√T1T2−T1
Thus, the time t it takes for sound waves to travel the distance L is:
t=2La⋅√T2−√T1T2−T1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.19videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.223videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
It takes 2.0 seconds for a sound wave to travel between two fixed points when the day temperature is 10∘C. If the temperature rise to 30∘C the sound wave travels between the same fixed parts in
View SolutionGraph between speed v of sound in air and pressure P at a constant temperature is given by
View Solution
Knowledge Check
- Question 1 - Select One
a=1,052+1.08t
The speed of a sound wave in air depends on the air temperature. The formula above shows the relationship between a, the speed of a sound wave, in feet per second, and t, the air temperature, in degrees Fahrenheit (.∘F).
Which of the following expresses the air temperature in terms of the speed of a sound wave?At=a−1,0521.08Bt=a+1,0521.08Ct=1,052−a1.08Dt=1.08a+1,052
How long will sound take to travel in (a) an iron rail and (b) air, both 3.3 km in length ? Take speed of sound in air to be 330 m s−1 and in iron to be 5280 m s−1.
View SolutionCalculate the minimum distance in air required between the source of sound and the obstacle to hear an echo. Take speed of sound in air = 350 ms−1
View SolutionA source of sound emitting waves at 360HZ is placed in front of a vertical wall, at a distance 2m from it. A detector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and the detestor for which the detector detects a maximum of sound. Take speed of sound in air=360m/s. Assume that there is not phase change in reflected wave.
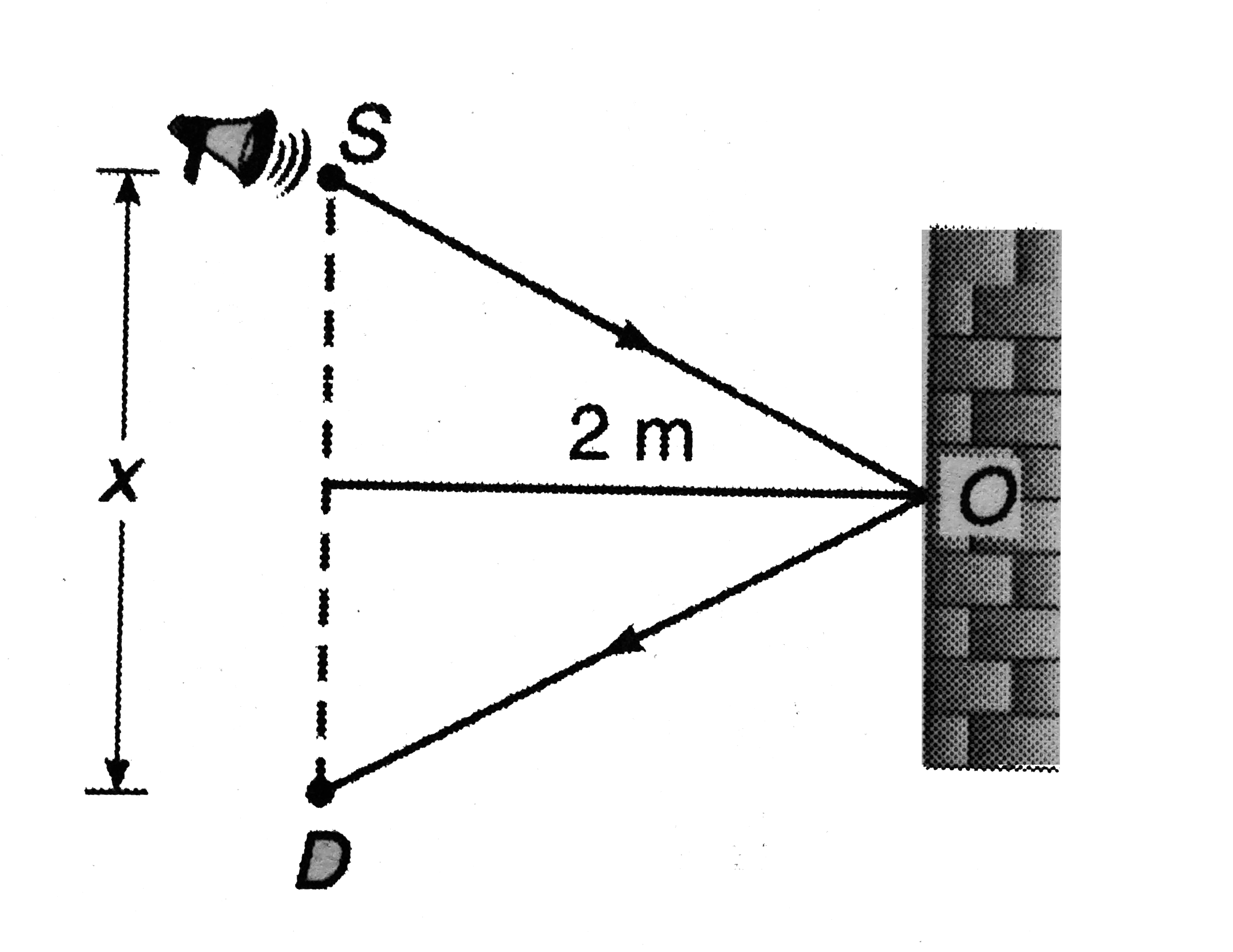 View Solution
View SolutionTwo friends A and B are standing a distance x apartin an open field and wind is blowing from A to B.A beats a drum and B hears the sound t1 timed after he sees the event. A and B intechange their positions and te experiment is repeated. This time B hears teh drum t2 time after he sees the event. Calculte teh velocity of sound in still air v and the velocity of wind u. Neglect the tiem light takes in travelling between the friends.
View SolutionThe relation between time t and distance x is t=ax2+bx where aandb are constants. The acceleration is
View SolutionThe intensities of two sound waves, one in air and the second one in water are equal (i) What is the ratio of the pressure amplitude of the wave in water to that of the wave in air? If the pressure amplitudes are equal instead, what is the ratio of the intensities of hte waves? Density of air is 1.293kg/m2. Velocity of sound in air and water are 330ms−1and1450ms−1 respectively.
View Solution(A): According to Laplace the propagation of sound in air is an adiabatic process.
(B): Pressure has no effect on velocity of sound in a gas as long as temperature remains constant.
(C): The velocity of sound in air changes by 0.61 m/s when temperature changes by 1∘CView Solution

