Graph between speed v of sound in air and pressure P at a constant temperature is given by
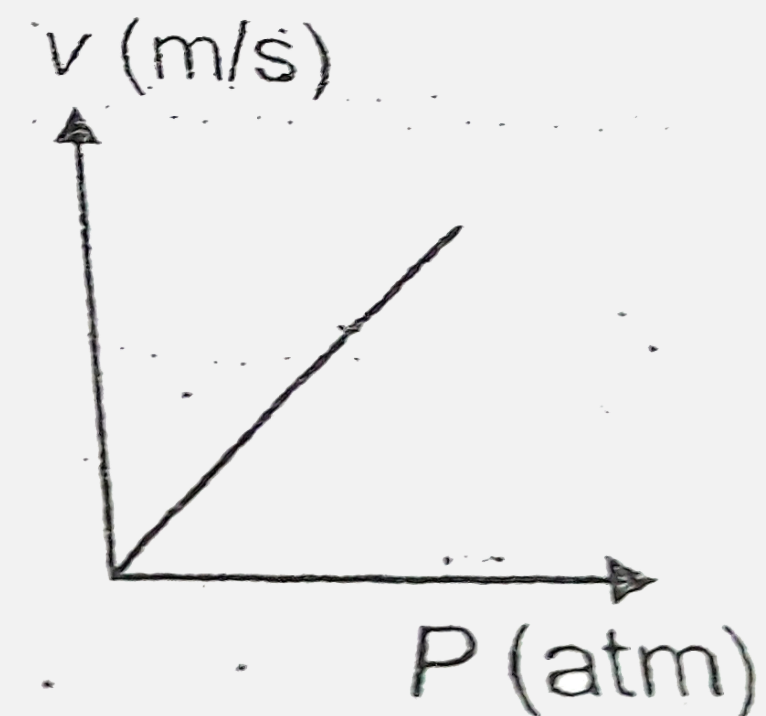
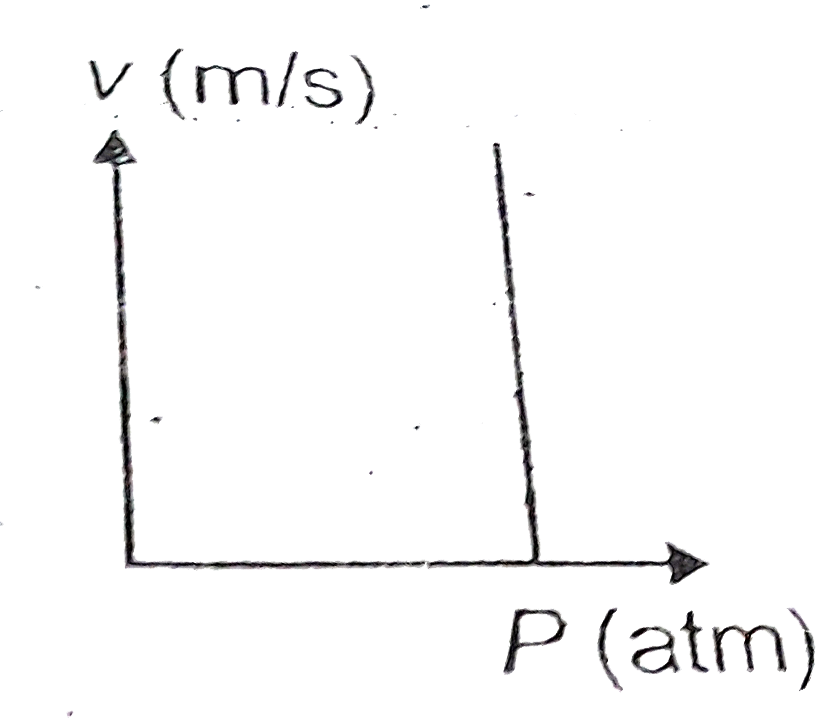


The correct Answer is:C
To solve the question regarding the graph between the speed v of sound in air and pressure P at a constant temperature, we can follow these steps:
Step 1: Understand the Formula for Speed of Sound
The speed of sound in a medium is given by the formula:
v=√γPρ
where:
- v is the speed of sound,
- γ is the adiabatic index (constant for a given gas),
- P is the pressure,
- ρ is the density of the medium.
Step 2: Relate Density and Pressure
For an ideal gas, the equation of state is given by:
PV=nRT
Rearranging this, we can express pressure in terms of density:
P=nRTV
Since n=mM (where m is mass and M is molar mass), we can express P as:
P=mRTMV
From the definition of density ρ=mV, we can substitute ρ into the equation:
P=ρ⋅RTM
Step 3: Establish a Relationship at Constant Temperature
At constant temperature, T and R are constants, which means:
Pρ=constant
This implies that if the pressure P increases, the density ρ must decrease to maintain the ratio constant.
Step 4: Substitute Back into the Speed of Sound Formula
Substituting Pρ back into the speed of sound formula:
v=√γPρ=√γ⋅constant
Since both γ and the ratio Pρ are constants, we can conclude that the speed of sound v remains constant as pressure changes.
Conclusion
Thus, the graph between the speed v of sound in air and pressure P at a constant temperature is a horizontal line, indicating that the speed of sound does not change with pressure at constant temperature.
Final Answer
The correct answer is that the speed of sound remains constant as pressure changes at constant temperature.
---
The speed of sound in a medium is given by the formula:
v=√γPρ
where:
- v is the speed of sound,
- γ is the adiabatic index (constant for a given gas),
- P is the pressure,
- ρ is the density of the medium.
For an ideal gas, the equation of state is given by:
PV=nRT
Rearranging this, we can express pressure in terms of density:
P=nRTV
Since n=mM (where m is mass and M is molar mass), we can express P as:
P=mRTMV
From the definition of density ρ=mV, we can substitute ρ into the equation:
P=ρ⋅RTM
At constant temperature, T and R are constants, which means:
Pρ=constant
This implies that if the pressure P increases, the density ρ must decrease to maintain the ratio constant.
Substituting Pρ back into the speed of sound formula:
v=√γPρ=√γ⋅constant
Since both γ and the ratio Pρ are constants, we can conclude that the speed of sound v remains constant as pressure changes.
Thus, the graph between the speed v of sound in air and pressure P at a constant temperature is a horizontal line, indicating that the speed of sound does not change with pressure at constant temperature.
The correct answer is that the speed of sound remains constant as pressure changes at constant temperature.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-B)35videos
WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-C)11videos
WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Try Yourself65videos
WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))1videos
WAVE OPTICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)13videos
WORK, ENERGY AND POWER
Similar Questions
State the speed of sound in air ?
View SolutionSpeed of sound waves in air
View SolutionSpeed of sound in a gas at constant temperature depends on
View SolutionThe variation of extent of adsorption with pressure at a given constant temperature is given in following figure
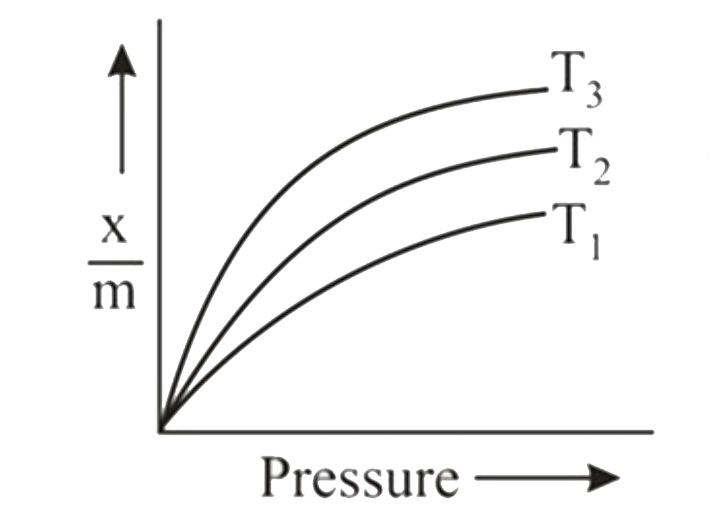
Which of the following relation between temperature of isotherms is correct ?View SolutionStatement-1: The speed of sound in humid air is more than the speed of sound in dry air keeping pressure constant.
Statement-2: Speed of sound in air with respect to air remains constant at a given temperature.
Statement-3: Transverse waves cannot be polarised.View SolutionIf va,vhandvm and are the speeds of sound in air, hydrogen and a metal at the same temperature, then
View SolutionAssertion: The plot of volume (V) versus pressure (P) at constant temperature is a hyperbola in the first quadrant.
Reason: V∝1/P at constant temperature.View SolutionA graph is plotted between pressure and volume at different temperatures . On the basis of the graph what changes will you observe in the volume if
(i) the pressure is increased at constant temperature .
(ii) the temperature is decreased at constant pressure .
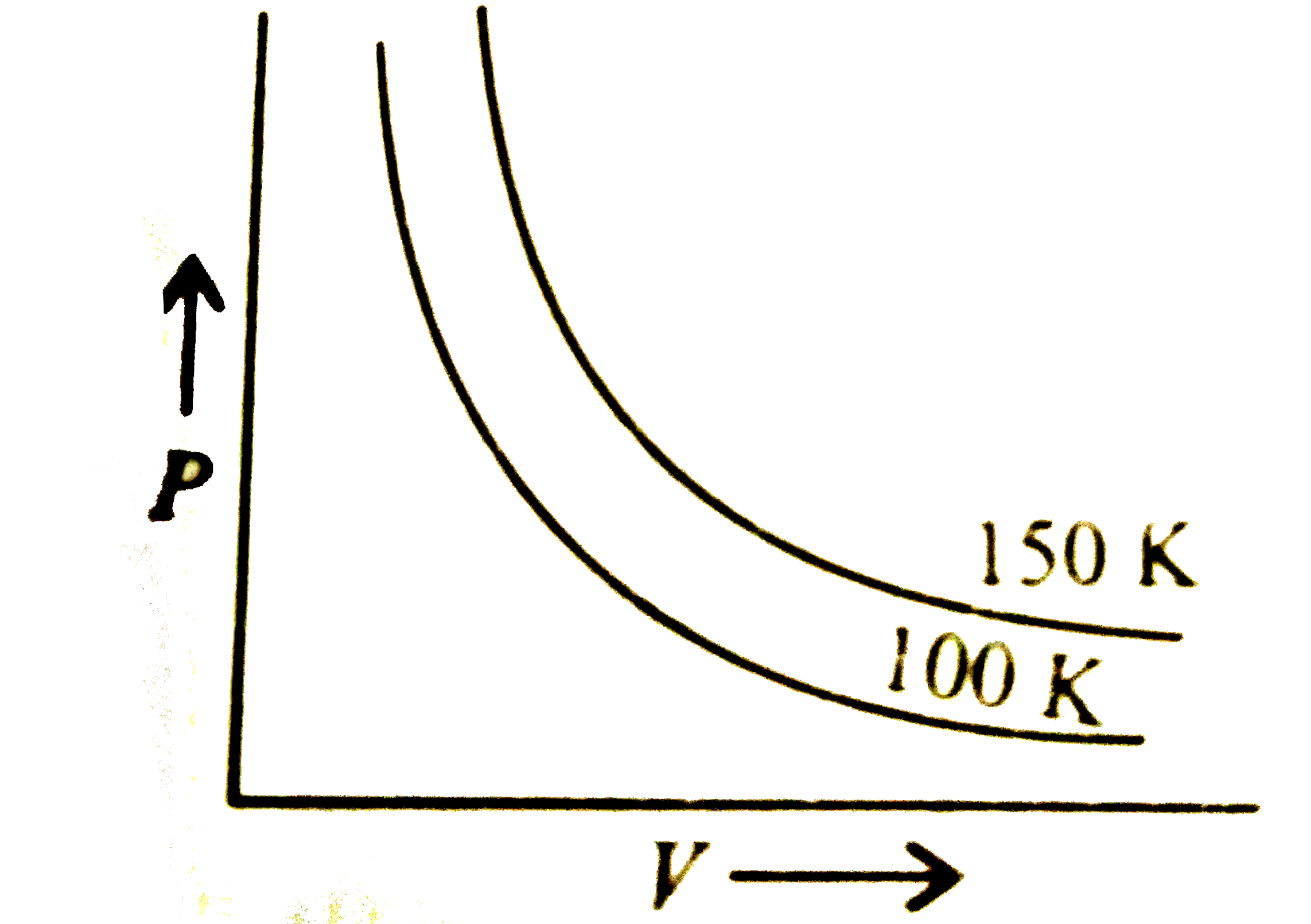 View Solution
View SolutionThe graph betwene P and V at constant temperature should look like
View SolutionHow does the speed of sound in air vary with temperature ?
View Solution

