The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
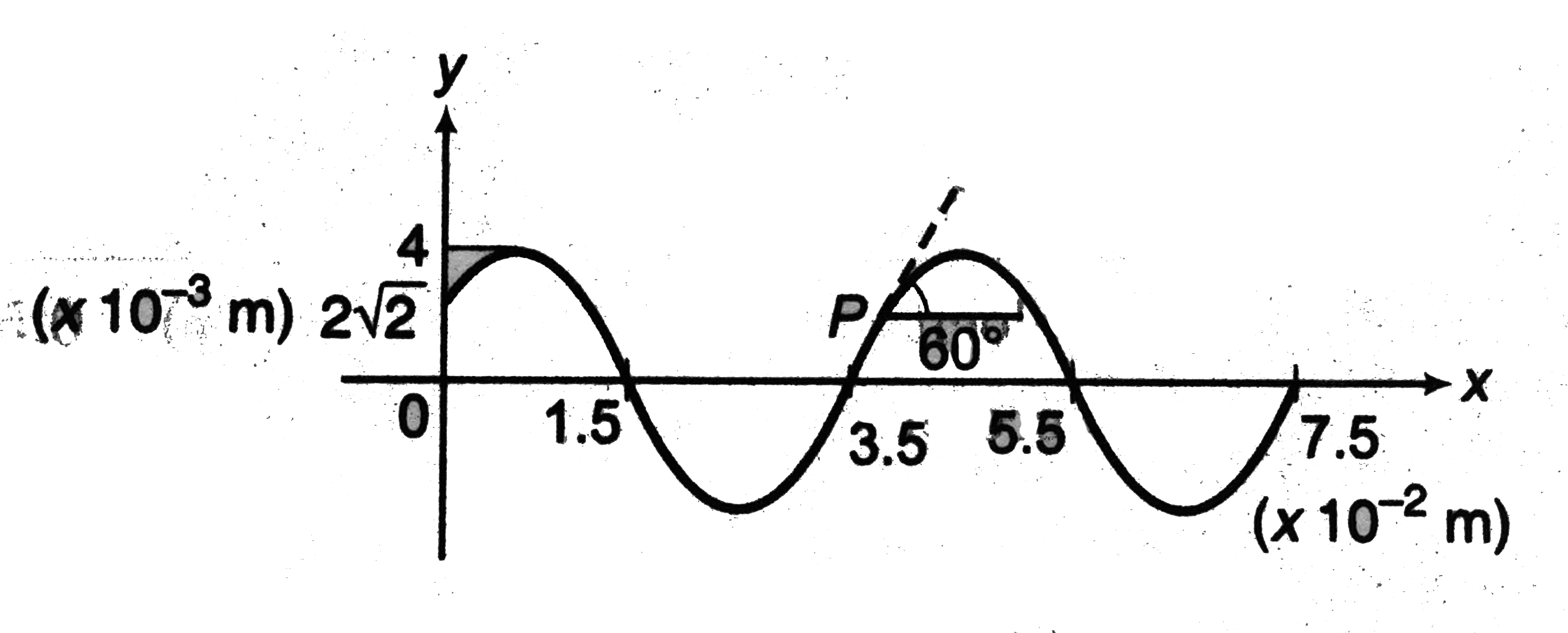
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
y5×10−3sin(10πt−50πx−π8)
y4×10−3sin(10πt−50πx−π8)
y(5×10−3(sin(10πt(50πx−π8)
y(4×10−3(sin(10πt(50πx−π8)
The correct Answer is:d
(a). At P: slope of tangent
=dydt=tan60∘=√3
particle velocity
vp=−vdydt⇒20√3=−v√3
⇒|v|=20cm/s=(1)(5)m/s
Hence, the wave is travelling in negative x-direction with velocity 20cm/s.
(b). Frome graph, amplitude A=4×10−3m
wave length λ=(5.5−1.5)=4×10−2m
wave number
K=2πλ=2π4×10−2=50πm−1
Angular frequency ω=kv
=50π×15=10π
Hence, equation can be written as
y=Asin(ωt+kx+ϕ)
=(4×10−3)sin(10πt+50πx+ϕ)
at =0,x=0
2√2×10−3=4×10−3sin(ϕ)
⇒sinϕ1√2,ϕ=π40,3π4
particle is moving up at t=0,x=0
Hence, ϕ=π4
Hence, equation is
y=(4×10−3)sin(10πt+50πx+π4)
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning
6 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
View SolutionFigure shows a snapshot for a travelling wave. The equation of wave at t=0 will be
_PHY_E06_334_Q01.png)
View SolutionA wave y=asin(ωt−kx) on a string meets with another wave producing a node at x=0. Then the equation of the unknown wave is
View SolutionWhen a wave moves in the direction of the vibrating Particles, it is called a longitudinal wave.
View SolutionThe following figure shows a wave propagating in a string. The speed of point A, which is 3 cm above the mean position is 7√3πcm/s at the moment shown. What is the speed of the wave in m/s?
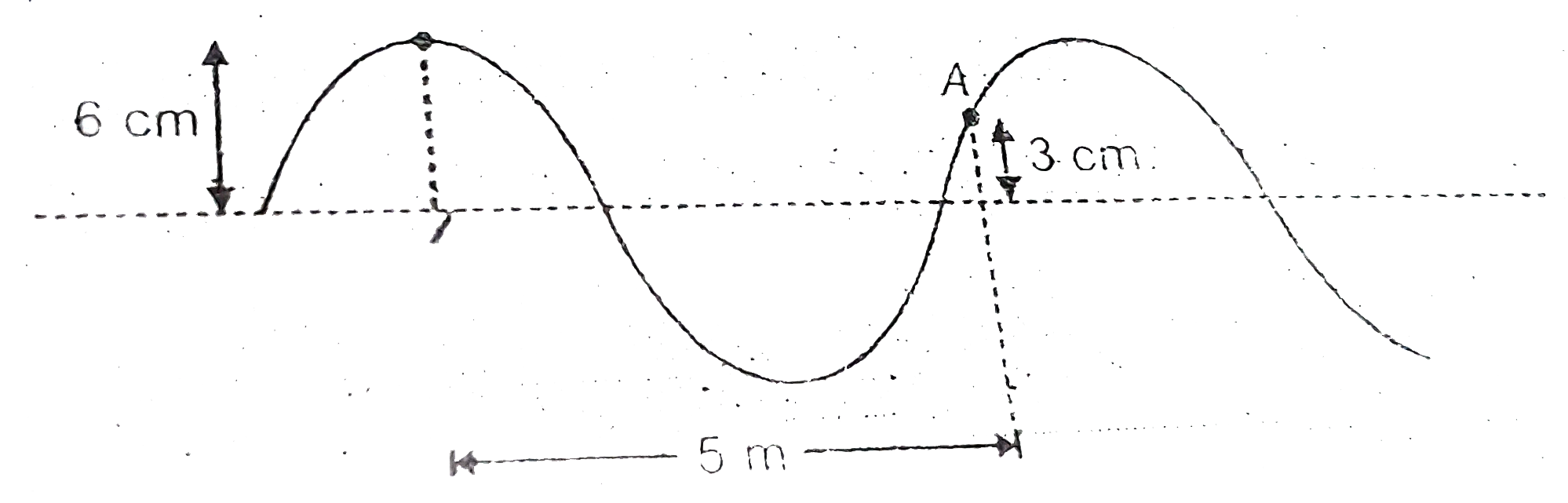
View SolutionA wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x)=Asin(xa), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time 1, if the wave speed is v.
View SolutionFigure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20cms−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
 .
.
View SolutionFigure shows a snapshot of a sinusoidal travelling wave taken at t=0.3s.The wavelength is 7.5cm and the amplitude is 2cm. If the crest P was at x=0at t=0, write the equation of travelling wave. ,

View SolutionThe frequency of the wave propagating on a string is 20Hz. What will be the difference in phase of a particle of the string in a time interval of 0.01 s ?
View SolutionFigure shows a plot of the transverse displacement of the particle of a string at t=0 through which a travelling wave is passing in the positive in the positive x-direction. The wave speed is 20cm/s. Find (a) the amplitude (b) the wavelength (c) the wave number and (d) the frequency of the wave.

View Solution
