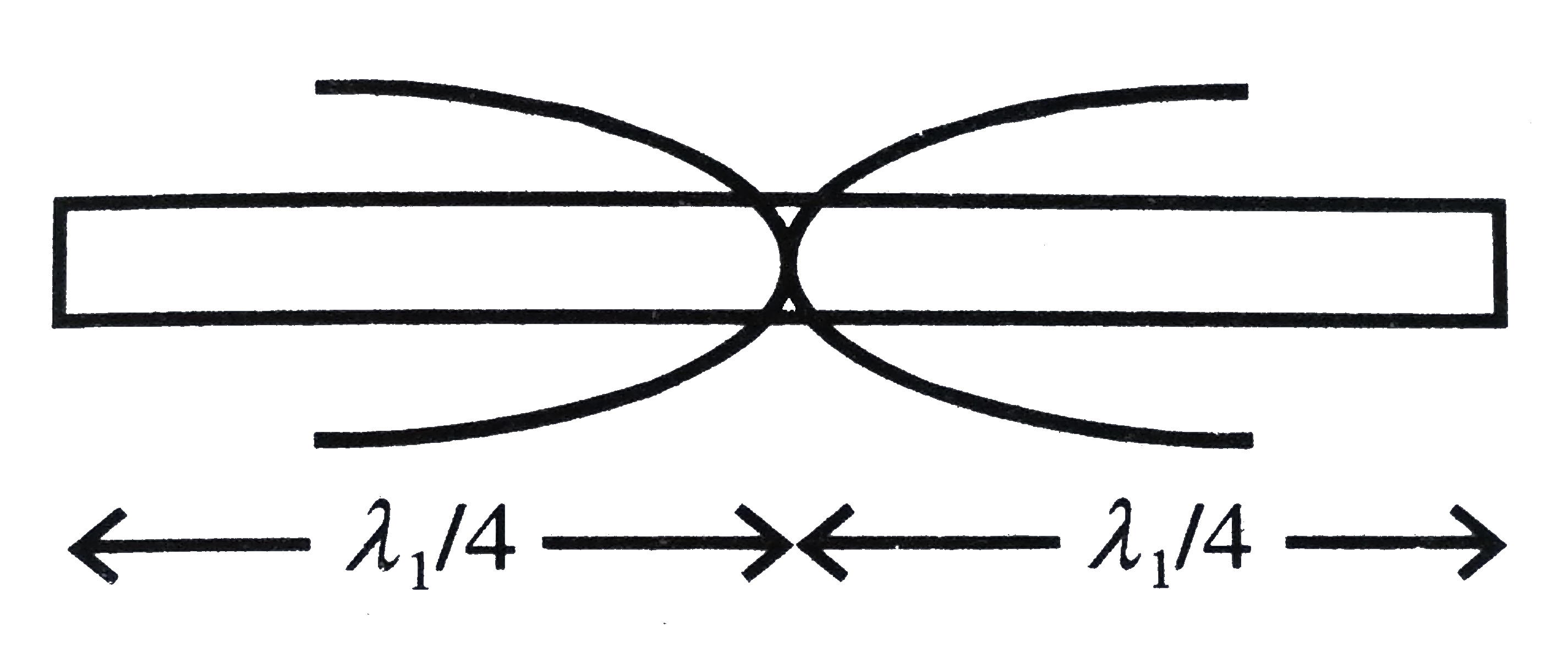
A rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
The correct Answer is:fn=2n−12l√Yρ,wheren=1,2,3….
Case I
l=2λ1/4andv=fλ1
V=√Yρ,l=λ1ρ,l=λ12
f1=vλ1=12l√Yρ
Case II
l=2[λ24+λ22]
l=3λ22
Again f2=vλ2=32l√Yρ
Cae III
l=25λ34,λ3=2l5
f3=vλ3=52l√Yρ
Comparing expression f1,f2,f3, we have
fn=2n−12l√Yρ , where n=1,2,3,..

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct144videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple26videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Exercise 7.232videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
A metal rod of length 1m is clamped at two points as shown in the figure. Distance of the clamp from the two ends are 5 cm and 15 cm, respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young's modulus of elasticity and density of aluminium are Y=1.6×1011Nm−2 and ρ=2500kgm−3 , respectively.
 View Solution
View SolutionA steel rod 100 cm long is clamped at its middle. The fundamental frequency of loungitudinal vibrations of the fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 KHz. What is the speed of soind in steel?
View SolutionA uniform rod of length 20 cm is clamped at the two points A and B as shown. Then the fundamental frequency of longitudinal vibration of the rod is (Y=2×1011N/m2,ρ=8×103kg/m3)
 View Solution
View SolutionA copper rod of length l=50cm is clamped at its midpoint. Find the number of natural longitudinal oscillations of the rod in the frequency range from 20 to 50kHz. What are those frequencies equal to ?
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec isView SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing stress developed in the rod isView SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing displacements of particles about their mean positions is.View SolutionAn aluminum rod having a length 100 cm is clamped at its middle point and set into longitudinal vibrations. Let the rod vibrate in its fundamental mode. The density of aluminum is 2600 kg/m3 and its Young's modulus is 7.8×1010N/m2. The frequency of the sound produced is :-
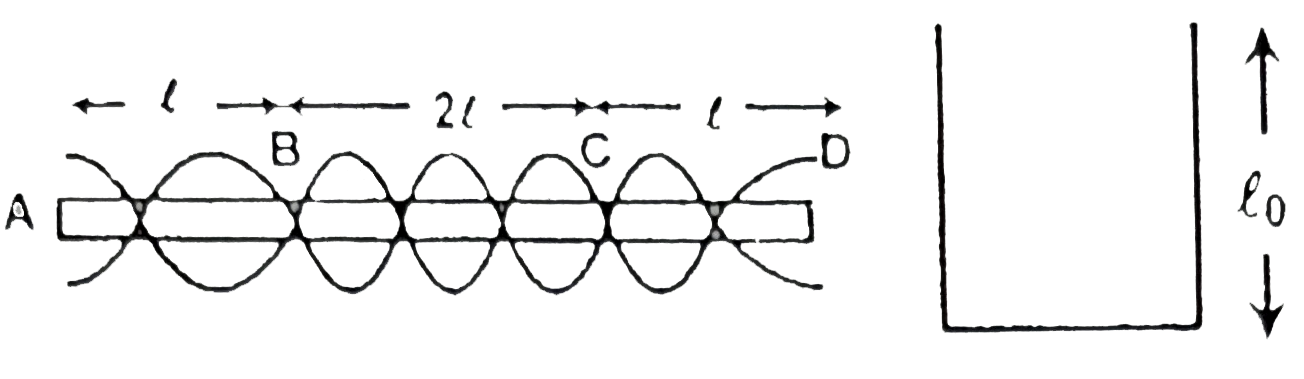
View SolutionA closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
 View Solution
View Solution

