To determine the young's modulus of a wire , the formula is Y=FA.LΔl , where L = l ength ,A = area of cross - section of the wire , ΔL = change in the length of the wire when streched with a force F. Find the conversion factor to change it from CGS t o MKS system.
1
10
0.1
0.01
The correct Answer is:C
Y=FA.L△L=dynecm2=10−5N10−4m2=0.1Nm2
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:Multiple correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Answer Correct Type
Explore 22 Videos
Similar Questions
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionA load w is suspended from a wire of length l and area of cross-section A. Change in length of the wire is say Δl. Change in length Δl can be increased to two times by increasing
View SolutionA wire of natural length l, young's modulus Y and area of cross-section A is extended by x. Then, the energy stored in the wire is given by
View SolutionA wire of cross-sectional area A breaks due to its own weight when length of the wire is l. If area of cross-section of the wire is made 3A then maximum length of the wire can be hung without breaking is
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionA wire fixed at the upper end stretches by length l by applying a force F. The work done in stretching is
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
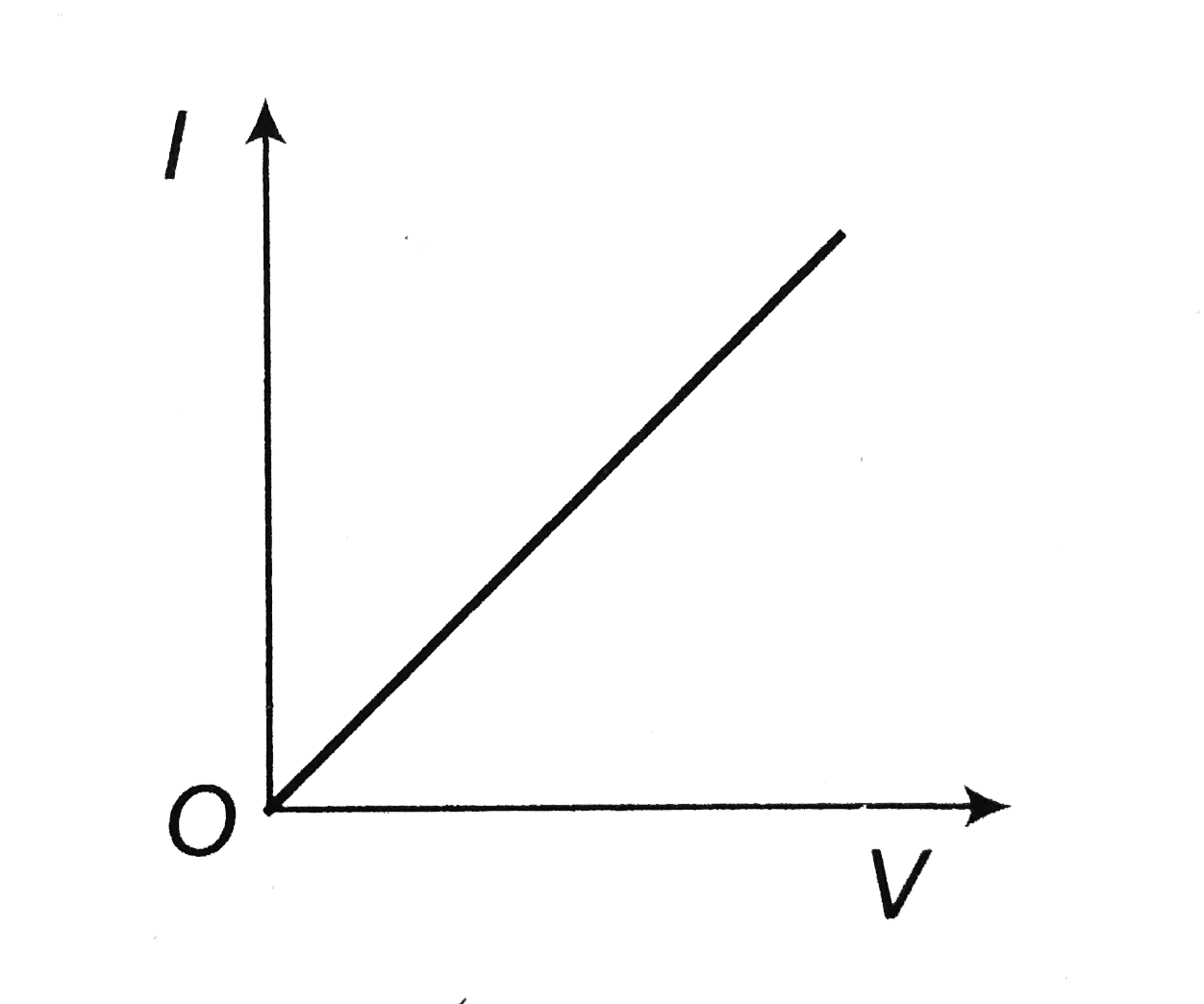
View SolutionThe length of an iron wire is L and area of cross-section is A. The increase in length is l on applying the force F on its two ends. Which of the statement is correct
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View Solution
