If and is finite, then
is parallel to
and are mutually perpendicular
The correct Answer is:C
To solve the problem, we start with the given condition:
|→V1+→V2|=|→V1−→V2|
Step 1: Square both sides
We square both sides of the equation to eliminate the magnitudes:
|→V1+→V2|2=|→V1−→V2|2
Step 2: Expand both sides
Using the property of magnitudes, we expand both sides:
(→V1+→V2)⋅(→V1+→V2)=(→V1−→V2)⋅(→V1−→V2)
This gives us:
→V1⋅→V1+2→V1⋅→V2+→V2⋅→V2=→V1⋅→V1−2→V1⋅→V2+→V2⋅→V2
Step 3: Simplify the equation
We can simplify the equation by canceling out the common terms:
→V1⋅→V1+→V2⋅→V2+2→V1⋅→V2=→V1⋅→V1+→V2⋅→V2−2→V1⋅→V2
This leads us to:
2→V1⋅→V2=−2→V1⋅→V2
Step 4: Combine like terms
Bringing all terms involving →V1⋅→V2 to one side gives:
2→V1⋅→V2+2→V1⋅→V2=0
This simplifies to:
4→V1⋅→V2=0
Step 5: Conclude about the vectors
Since 4→V1⋅→V2=0, we conclude that:
→V1⋅→V2=0
This means that the vectors →V1 and →V2 are perpendicular to each other.
Final Answer
Thus, the correct conclusion is that →V1 and →V2 are mutually perpendicular.
Similar Questions
Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
View SolutionLet →a→band→c be non- zero vectors aned →V1=→a×(→b×→c)and→V2=(→a×→b)×→c.vectors →V1and→V2 are equal . Then
View SolutionAssertion: An observer is moving due east and wind appears him to blow from north. Then the actual direction of air blow must be towards south-east
Reason: →VR=→VA−→VM where →VR is the relative velocity of wind w.r.t. man. →VA= actual velocity of wind (w.r.t. ground) and →VM= velocity of man w.r.t. ground.View SolutionIf →uand→v are unit vectors and θ is the acute angle between them, then 2→u×3→v is a unit vector for
View SolutionIf →uand→v are unit vectors and θ is the acute angle between them, then 2→u×3→v is a unit vector for
View SolutionIf →uand→v are unit vectors and θ is the acute angle between them, then 2u→u×3→v is a unit vector for
View SolutionIf →u=→a−→b, →v=→a+→b and |→a|=∣∣→b∣∣=2, then |→u×→v| is equal to
View SolutionTwo particles A,B are moving on two concentric circles of radii R1 and R2 with equal angular speed ω. Att=0,their positions and direction of motion are shown in the figure. The relative velocity →Va−→Vb at t=π/2ω is given by :
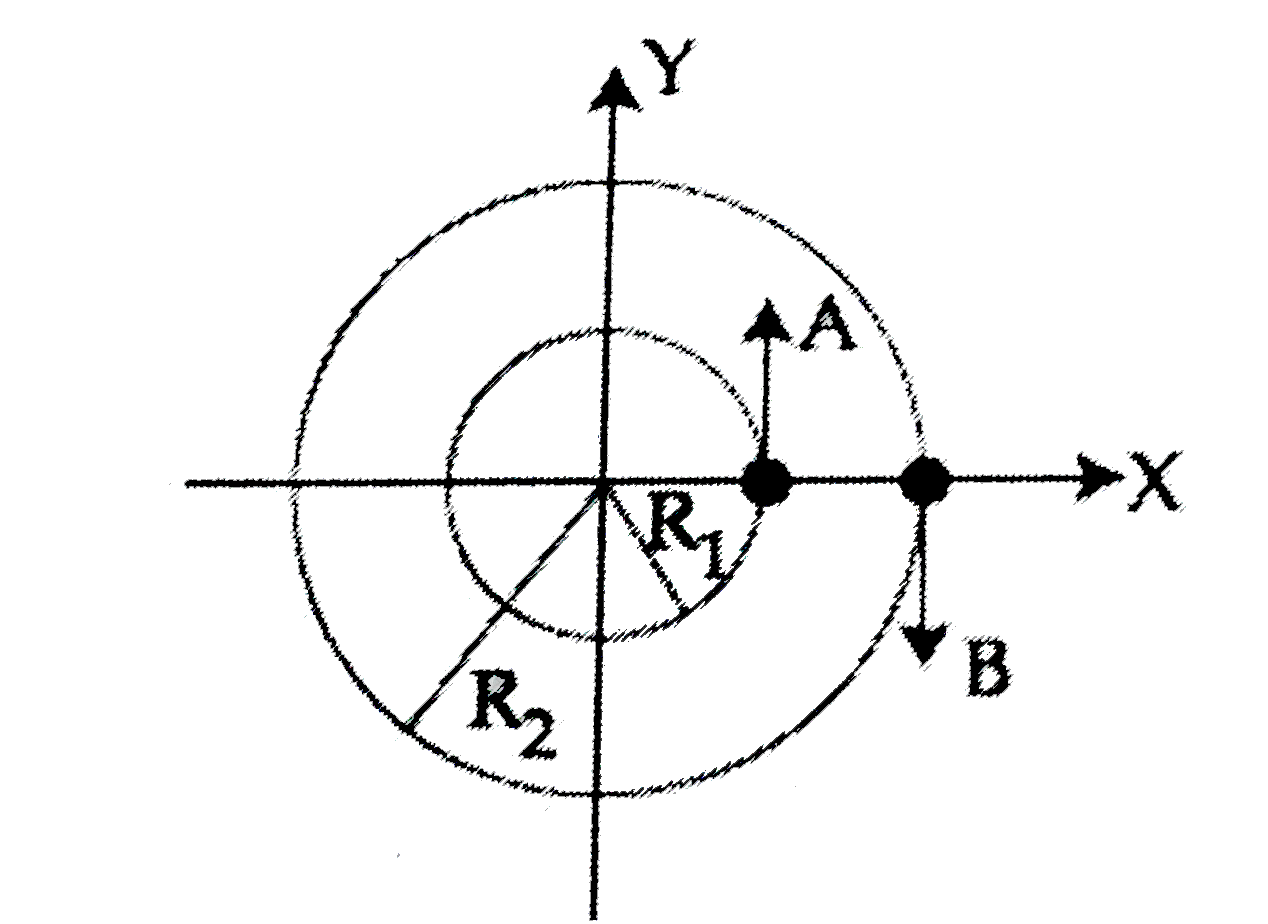 View Solution
View SolutionLet →u,→vand→w be such that |→u|=1,|→v|=2and|→w|=3 if the projection of →v along →u is equal to that of →w along →u and vectors →vand→w are perpendicular to each other then |→u−→v+→w| equals
View SolutionIf uandv are two non-collinear unit vectors such that |→u×→v|=∣→u−→v2∣∣∣ , then the value of ∣ →u×(→u×→v)∣∣2 is equal to
View Solution

