
System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
9ms
12ms
9×54ms
none of these
The correct Answer is:B

9cosα=vsinα→ ..(i)
19−R12=tanα
(R+5)=(12)2+(19−R)2 ..(ii)
⇒R=10
Hence from (i) and (ii) v=12ms
Similar Questions
A system is shown in the figure. Block A moves with velocity 10m/s. The speed of the mass B will be :
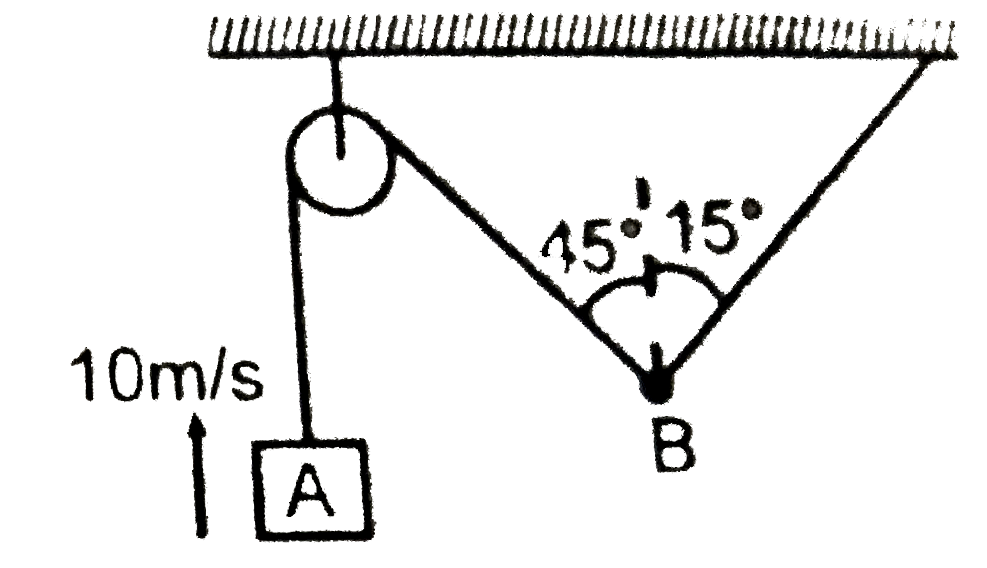
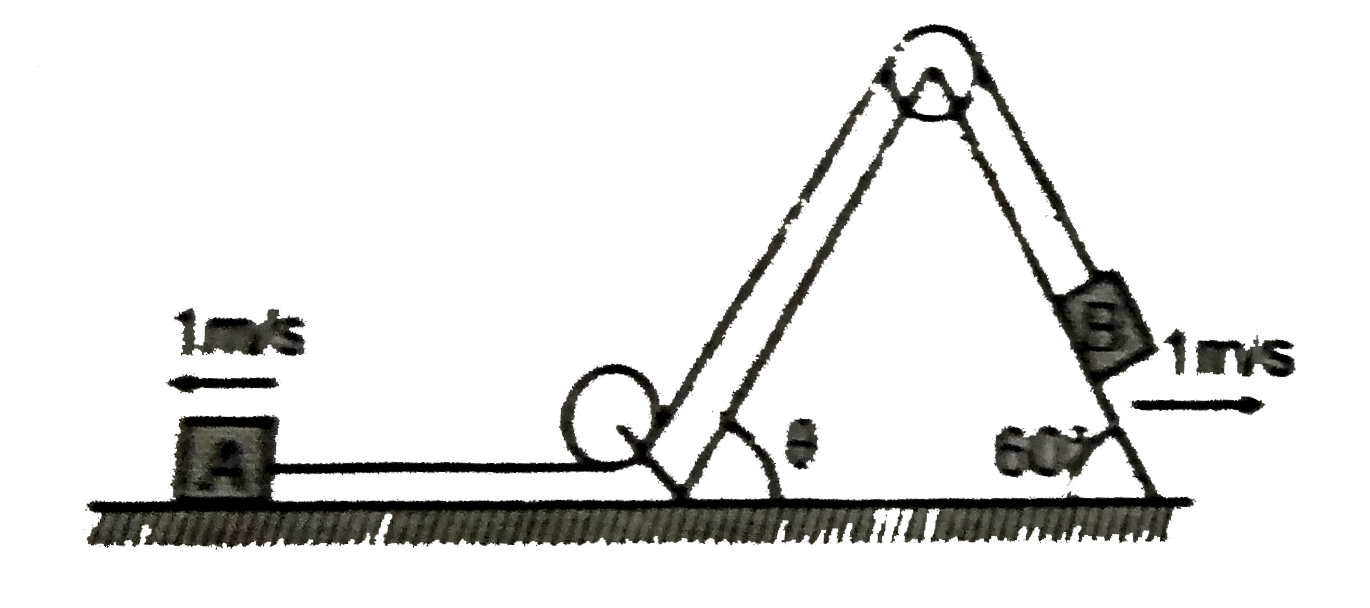
View SolutionA system is shown in the figure. Block A is moving with 1m/s towards left. Wedge is moving with 1m/s towards right. Then speed of the block B will be :
View SolutionConsider a system composed of two metallic spheres of radii r1andr2 conneced by a thin wire and switch S as shown in the figure. Initially S is in open position. And the spheres carry charges q1andq2 respectively. If the switch is closed, the potential of the system is

View SolutionA hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Coordinate of the point having the maximum pressure is
View SolutionA solid uniformly charged ficed non-conducting sphere of total charge Q and radius R contains a tunnel of negligible diameter. If a point charge '-q' of mass 'm' is released at rest from point P as shown in figure then find out its velocity at following points

(i) At the surface of sphere
(ii) At the centre of the sphere
View SolutionA hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Consider points A and B as shown in the figure.
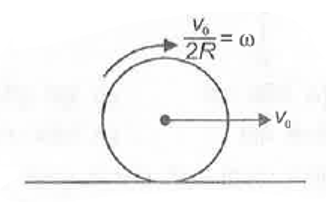
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)

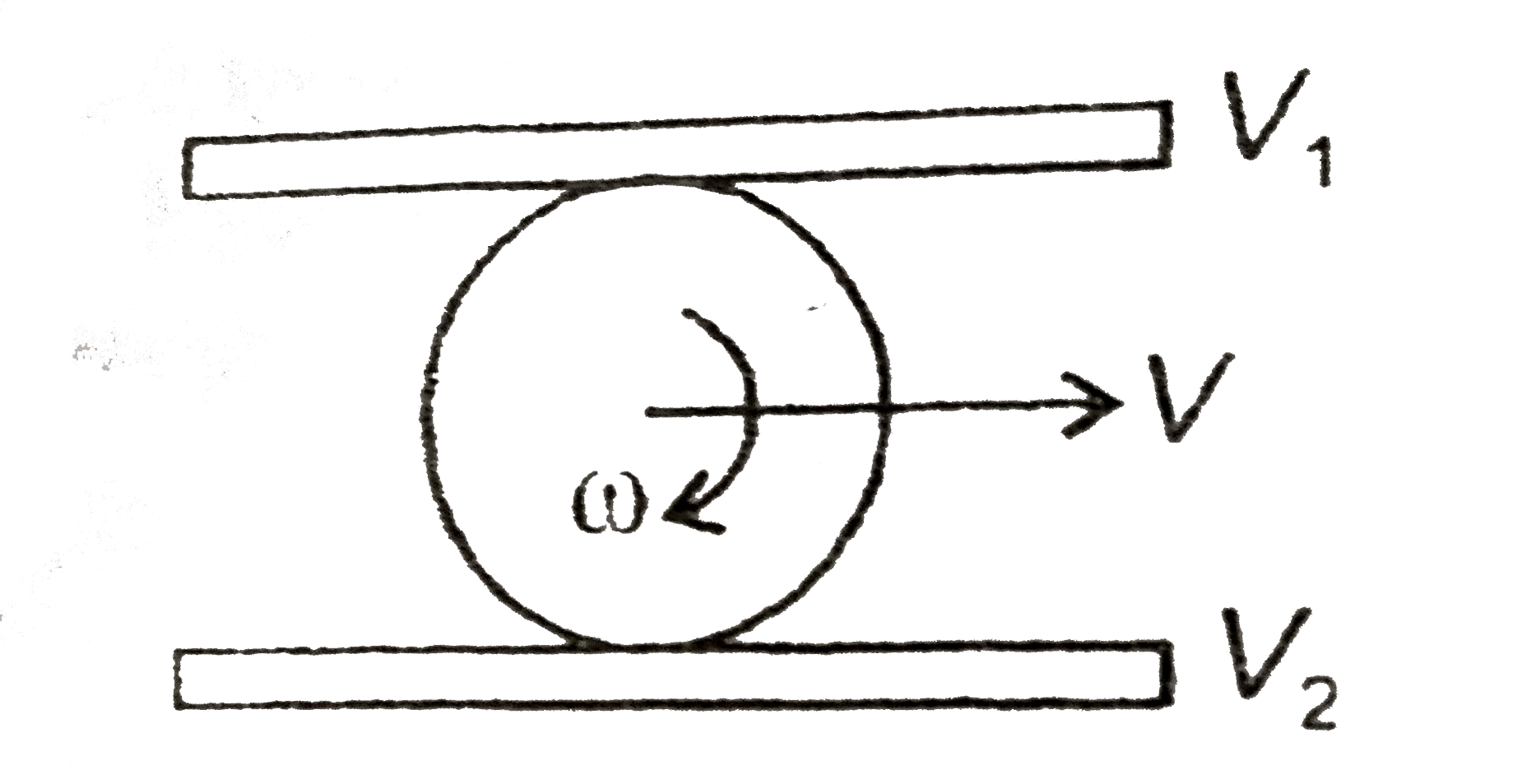
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View Solution
