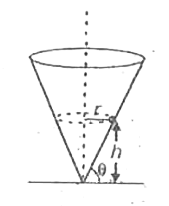
A particle describes a horizontal circle in a conical funne whoses inner surface is smooth with speed of 0.5m/s . What is the height of the plane of circle from vertex the funnel?
0.25 cm
2 cm
4 cm
2.5 cm
The correct Answer is:D
To solve the problem of finding the height of the plane of the circle from the vertex of the conical funnel, we will follow these steps:
1. Understanding the Forces Acting on the Particle:
- The particle is moving in a horizontal circle inside a conical funnel. The forces acting on the particle are:
- Gravitational force (weight) acting downwards: mg
- Normal force N acting perpendicular to the surface of the funnel.
2. Identifying the Geometry:
- Let h be the height of the circular path from the vertex of the funnel, and r be the radius of the circular path.
- The angle between the radius of the funnel and the vertical line is θ.
3. Using Trigonometric Relationships:
- From the geometry of the funnel, we can relate the radius r and height h using the tangent function:
tanθ=rh
4. Setting Up the Equations of Motion:
- In the vertical direction, the vertical component of the normal force must balance the weight of the particle:
Ncosθ=mg(1)
- In the horizontal direction, the horizontal component of the normal force provides the necessary centripetal force:
Nsinθ=mv2r(2)
5. Dividing the Two Equations:
- Dividing equation (1) by equation (2):
NsinθNcosθ=mv2rmg
- This simplifies to:
tanθ=v2gr
6. Substituting the Value of tanθ:
- From the earlier relationship, we have tanθ=rh. Therefore:
rh=v2gr
- Rearranging gives:
r2=v2hg
7. Finding the Height h:
- Rearranging the equation gives:
h=gr2v2
8. Substituting Known Values:
- Given v=0.5m/s and g=10m/s2:
- We need to find r in terms of h. From the earlier equations, we can express r in terms of h:
h=v2g=(0.5)210=0.2510=0.025m
- Converting to centimeters:
h=0.025×100=2.5cm
Final Answer:
The height of the plane of the circle from the vertex of the funnel is 2.5 cm.
- The particle is moving in a horizontal circle inside a conical funnel. The forces acting on the particle are:
- Gravitational force (weight) acting downwards: mg
- Normal force N acting perpendicular to the surface of the funnel.
- Let h be the height of the circular path from the vertex of the funnel, and r be the radius of the circular path.
- The angle between the radius of the funnel and the vertical line is θ.
- From the geometry of the funnel, we can relate the radius r and height h using the tangent function:
tanθ=rh
- In the vertical direction, the vertical component of the normal force must balance the weight of the particle:
Ncosθ=mg(1)
- In the horizontal direction, the horizontal component of the normal force provides the necessary centripetal force:
Nsinθ=mv2r(2)
- Dividing equation (1) by equation (2):
NsinθNcosθ=mv2rmg
- This simplifies to:
tanθ=v2gr
- From the earlier relationship, we have tanθ=rh. Therefore:
rh=v2gr
- Rearranging gives:
r2=v2hg
- Rearranging the equation gives:
h=gr2v2
- Given v=0.5m/s and g=10m/s2:
- We need to find r in terms of h. From the earlier equations, we can express r in terms of h:
h=v2g=(0.5)210=0.2510=0.025m
- Converting to centimeters:
h=0.025×100=2.5cm
The height of the plane of the circle from the vertex of the funnel is 2.5 cm.
Similar Questions
A particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
View SolutionA particle describes a horizontal circle on the smooth surface of an inverted cone, the height of the plane of the circle above the vertex is 9.8 cm. Find the speed of the particle (g= 9.8m/s2) [See Fig.] (a) given in the answer section]
View SolutionA particle of mass m describes a circle of radius r . The centripetal acceleration of the particle is 4r2 . What will be the momentum of the particle ?
View SolutionA cylinder rolls on a horizontal plane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
View SolutionA particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The heigh of the plane of motion above the vertex is hh and the semi-vertical angle of the cone is α The period of revolution of the particle

View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
View SolutionA particle of mass 1kg is moving about a circle of radius 1m with a speed of 1m/s. Calculate the angular momentum of the particle.
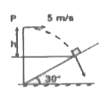
View SolutionA particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View Solution
