A particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
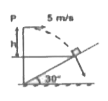
3.75m
5.0m
4.75m
0.417m
The correct Answer is:A
Step by step video & image solution for A particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5 m//s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30^(@) with the horizontal. Then, the height h shown in the figure is ( Take g = 10 m//s^(2) ) . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
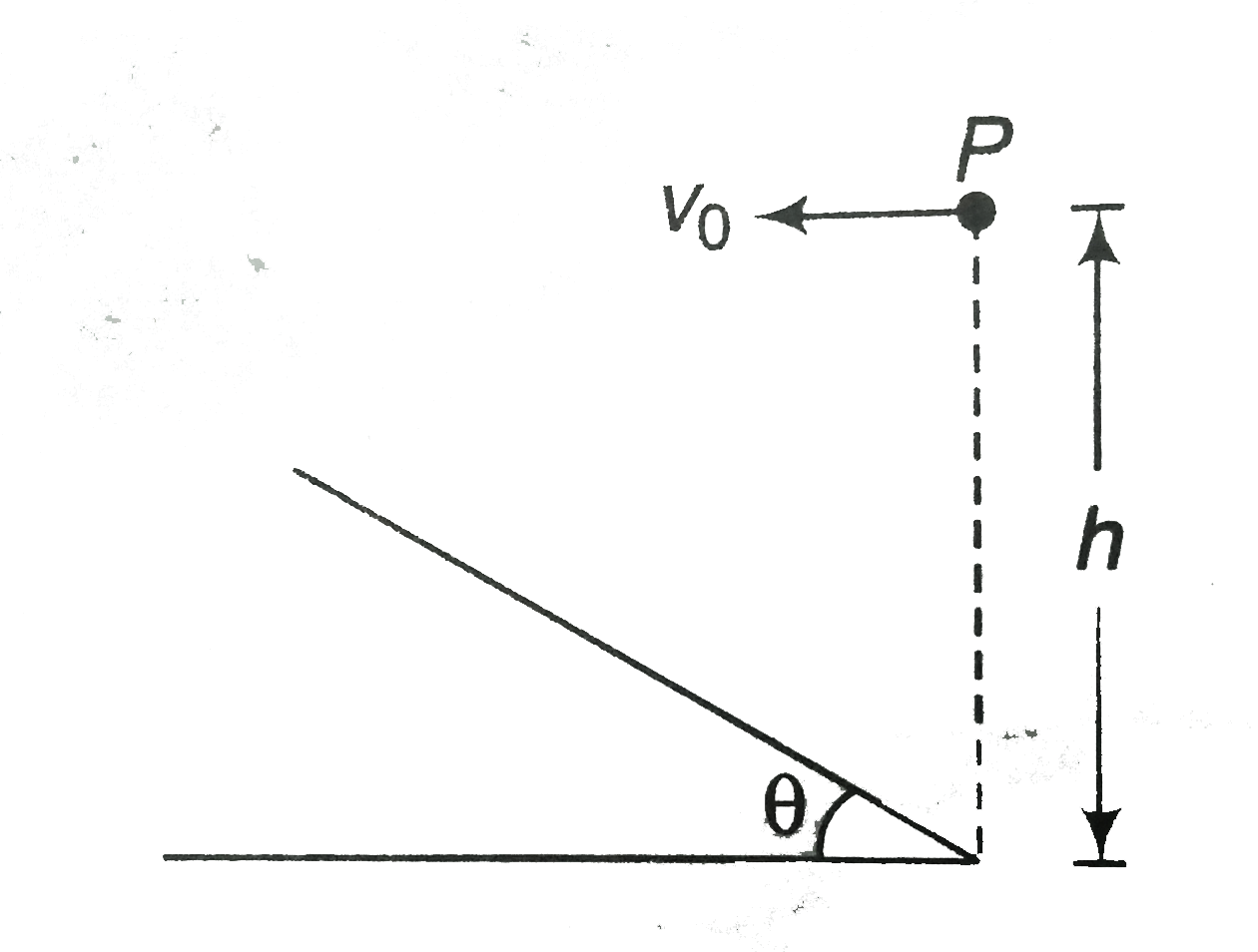
View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
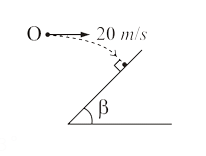
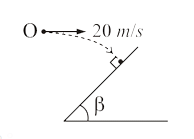
View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The speed of ball just before striking the plane is:
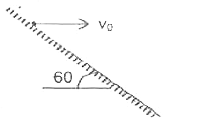
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The displacement of ball in two seconds will be:
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA particle of mass m is doing horizontal circular motion with the help of a string (conical pendulum) as shown in the figure. If speed of the particle is constant then,
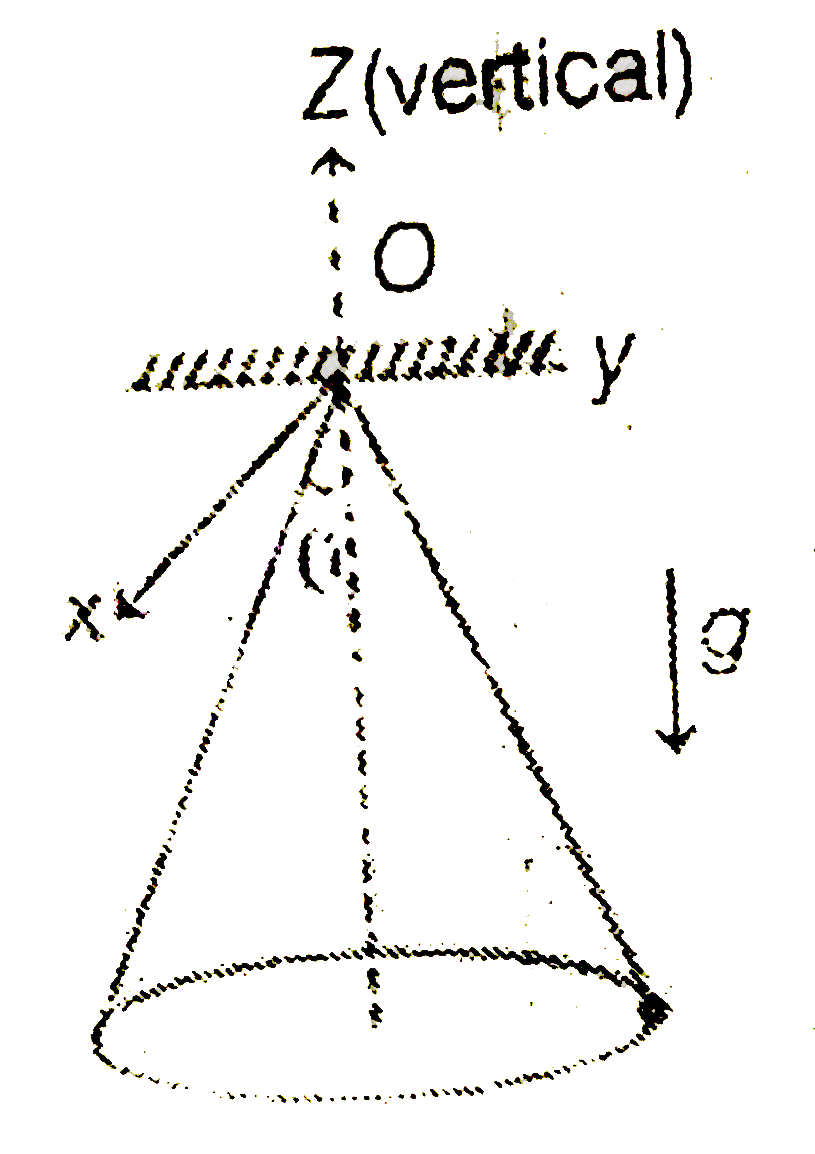
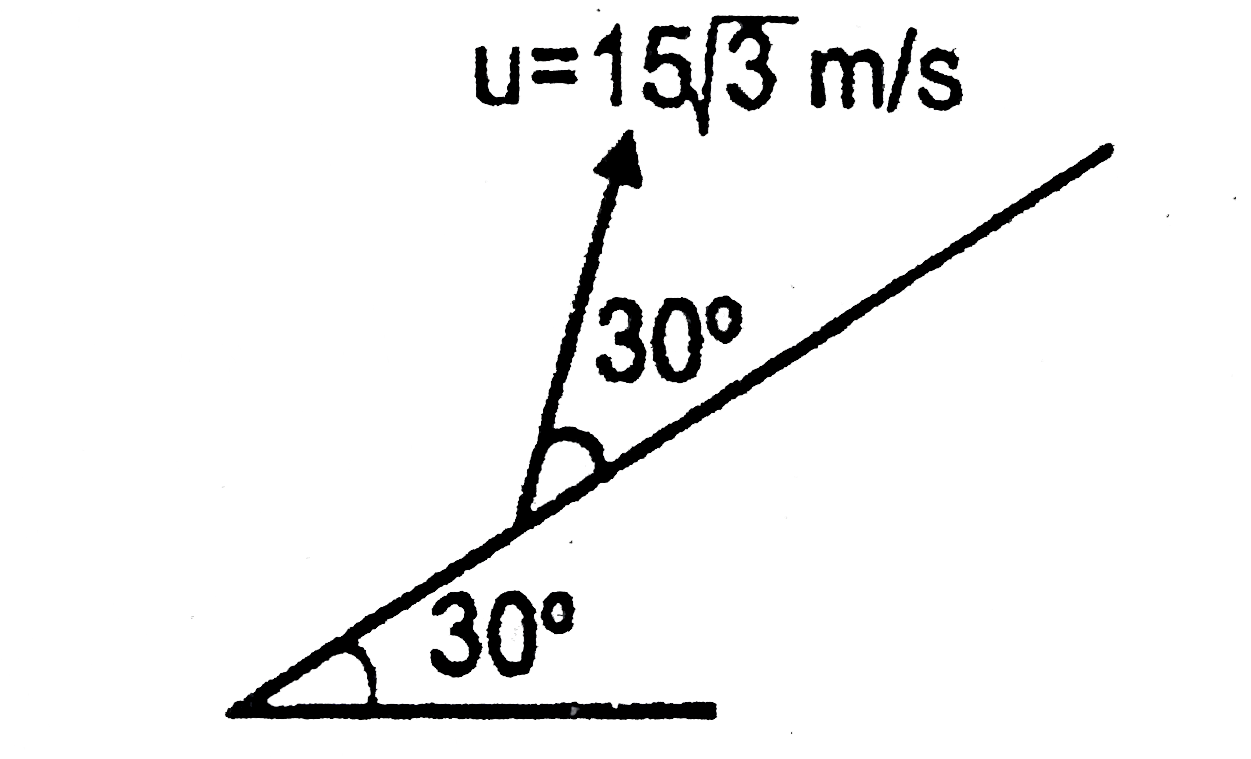
View SolutionA partile is projected up an incline (inclination angle =30∘) with 15√3m/s at an angle of 30∘ with the incline (as shown in figure) (g=10m/s2)
View SolutionA particle of mass m is given initial horizontal velocity of magnitude u as shown in the figure. It transfers to the fixed inclined plane without a jump, that is, its trajectory changes sharply from the horizontal line to the inclined line. All the surfaces are smooth and90∘≥θ>0∘. Then the height to which the particle shall rise on the inclined plane (assume the length of the inclined plane to be very large)

View SolutionA particle of mass m is given initial horizontal velocity of magnitude u as shown in the figure. It transfers to the fixed inclined plane without a jump, that is, its trajectory changes sharply from the horizontal line to the inclined line. All the surfaces are smooth adn 90∘≥θ>0∘. Then the height to which the particle shamm rise on the inclined plane (assume the length of the inclined plane to be very large)

View Solution
