If two balls of given masses and charges are released, which of the following is the correct arrangement in equilibrium?
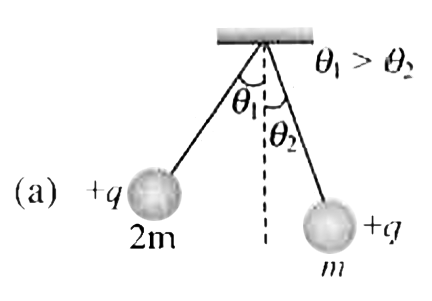
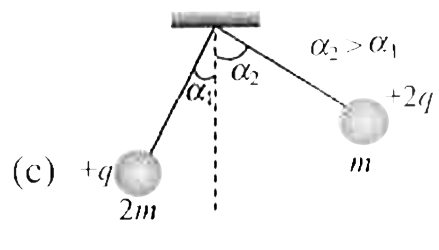
The correct Answer is:C, D
To solve the problem of determining the correct arrangement of two charged balls in equilibrium, we can follow these steps:
Step 1: Understand the Forces Acting on the Balls
When two balls with charges and masses are released, they will experience gravitational force (weight) acting downwards and electrostatic force due to their charges acting horizontally. The tension in the string will balance these forces.
Step 2: Analyze the Forces on Each Ball
For each ball, we can break down the forces into components:
- For the first ball (mass = 2m, charge = q1):
- Vertical component: Tcos(θ1)=2mg
- Horizontal component: Tsin(θ1)=F (where F is the electrostatic force)
- For the second ball (mass = m, charge = q2):
- Vertical component: T′cos(θ2)=mg
- Horizontal component: T′sin(θ2)=F
Step 3: Set Up the Equations
From the vertical components, we can express the tension:
- For the first ball: T=2mgcos(θ1)
- For the second ball: T′=mgcos(θ2)
From the horizontal components, we can equate the forces:
- Tsin(θ1)=T′sin(θ2)=F
Step 4: Relate the Angles Using Tangent
Using the relationships derived from the tension equations:
- tan(θ1)=F2mg
- tan(θ2)=Fmg
Step 5: Compare the Angles
From the equations for tangent:
- Since tan(θ2)=2tan(θ1), it follows that:
- tan(θ2)>tan(θ1)
- Therefore, θ2>θ1
Step 6: Evaluate the Given Options
Now we can evaluate the options provided in the question:
- If θ1>θ2 is given, that is incorrect.
- If θ2>θ1 is given, that is correct.
- If both angles are equal, that is incorrect.
- If both masses experience the same forces, that is correct.
Conclusion
The correct arrangements in equilibrium are options C and D, where the angles and forces are consistent with our analysis.
---
When two balls with charges and masses are released, they will experience gravitational force (weight) acting downwards and electrostatic force due to their charges acting horizontally. The tension in the string will balance these forces.
For each ball, we can break down the forces into components:
- For the first ball (mass = 2m, charge = q1):
- Vertical component: Tcos(θ1)=2mg
- Horizontal component: Tsin(θ1)=F (where F is the electrostatic force)
- Vertical component: T′cos(θ2)=mg
- Horizontal component: T′sin(θ2)=F
From the vertical components, we can express the tension:
- For the first ball: T=2mgcos(θ1)
- For the second ball: T′=mgcos(θ2)
- Tsin(θ1)=T′sin(θ2)=F
Using the relationships derived from the tension equations:
- tan(θ1)=F2mg
- tan(θ2)=Fmg
From the equations for tangent:
- Since tan(θ2)=2tan(θ1), it follows that:
- tan(θ2)>tan(θ1)
- Therefore, θ2>θ1
Now we can evaluate the options provided in the question:
- If θ1>θ2 is given, that is incorrect.
- If θ2>θ1 is given, that is correct.
- If both angles are equal, that is incorrect.
- If both masses experience the same forces, that is correct.
The correct arrangements in equilibrium are options C and D, where the angles and forces are consistent with our analysis.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answers Type
2 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension Type
2 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Which of the following is correct about the chemical equilibrium ?
View SolutionFor a reaction at equilibrium which of the following is correct ?
View SolutionA ball falls towards the earth. Which of the following is correct?
View Solutionwhich is correct at equilibrium ?
View SolutionFor a reversible system at equilibrium, which of the following is correct
View SolutionWhich of the following is correct for the molecules of a gas in thermal equilibrium ?
View Solutiontwo pith balls each with mass m are suspended from insulating threads. When the pith balls are given equal positive charge Q, they hang in equilibirum as shown. We now increase the charge on the left pith ball from Q to 2Q while leaving its mass essentially unchanged. Which of he following diagrams best represent the new equilibrium configuration?
View SolutionMid way between the two equal and similar charges , we place the third equal and similar charge. Which of the following statements is correct , concerned to the equilibrium along , the line joining the charges ?
View SolutionWhich of the following are arranged in correct increasing order of solubilities ?
View SolutionIf a charge is released in electric field, will it follow lines of force ?
View Solution
