Charges 4Q, q and Q and placed along x-axis at positions and , respectively. Find the value of q so that force on charge Q is zero
Q
Q/2
The correct Answer is:D
To solve the problem, we need to find the value of charge q such that the net force acting on charge Q is zero. The charges are placed along the x-axis at the following positions:
- Charge 4Q is at x=0
- Charge q is at x=12
- Charge Q is at x=1
1. Identify the Forces Acting on Charge Q:
- The force F1 due to charge 4Q on charge Q is repulsive (since both charges are positive).
- The force F2 due to charge q on charge Q will be attractive if q is negative (since Q is positive).
2. Calculate the Magnitude of the Forces:
- The distance between 4Q and Q is 1 unit. Thus, the force F1 is given by:
F1=k(4Q)(Q)(1)2=4kQ2
- The distance between q and Q is 12 unit. Thus, the force F2 is given by:
F2=k(q)(Q)(12)2=k(q)(Q)14=4kqQ
3. Set the Forces Equal to Each Other:
- For the net force on charge Q to be zero, we set the magnitudes of the forces equal:
F1=F2
4kQ2=4kqQ
4. Simplify the Equation:
- We can cancel 4k from both sides (assuming k≠0):
Q2=qQ
5. Solve for q:
- Dividing both sides by Q (assuming Q≠0):
q=Q
6. Determine the Sign of q:
- Since the force F1 is repulsive, F2 must be attractive to balance it. This means q must be negative. Therefore, we conclude:
q=−Q
Final Answer:
The value of q such that the force on charge Q is zero is:
q=−Q
- Charge q is at x=12
- Charge Q is at x=1
- The force F1 due to charge 4Q on charge Q is repulsive (since both charges are positive).
- The force F2 due to charge q on charge Q will be attractive if q is negative (since Q is positive).
- The distance between 4Q and Q is 1 unit. Thus, the force F1 is given by:
F1=k(4Q)(Q)(1)2=4kQ2
- The distance between q and Q is 12 unit. Thus, the force F2 is given by:
F2=k(q)(Q)(12)2=k(q)(Q)14=4kqQ
- For the net force on charge Q to be zero, we set the magnitudes of the forces equal:
F1=F2
4kQ2=4kqQ
- We can cancel 4k from both sides (assuming k≠0):
Q2=qQ
- Dividing both sides by Q (assuming Q≠0):
q=Q
- Since the force F1 is repulsive, F2 must be attractive to balance it. This means q must be negative. Therefore, we conclude:
q=−Q
The value of q such that the force on charge Q is zero is:
q=−Q
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answers Type
2 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension Type
2 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Point charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and x=2a respectively, then
View SolutionIn the configuration as shown +q charge is placed at origin and Q and Q are placed at distance a and a0 respectively from origin. If net electrostatic force on charge (+q) is along negative y-axis and θ=θ2/2, then (Q/Q) is equal to:
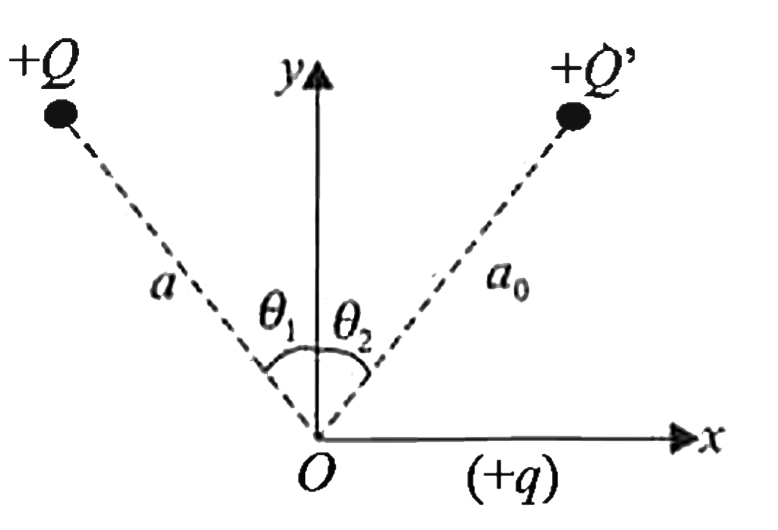
View SolutionPoint charges q1 and q2 lie o the x-axis at points x=−a and x=+a respectively.
a. How must q1 and q2 be related for the net electrostatic force on point charge +Q, placed at x=+a2, to be zero?
b. With the same point charge +Q now placed ate x=+3a/2
View SolutionIn the figure, two point charges +qand−q are placed on the x-axis at (+a,0)and(−a,0) respectively. A tiny dipole of dipolem moment (p) is kept at the origin along the y-axis. The torque on the dipole equals

View SolutionThe charges - q, Q, -q are placed along x-axis at x = 0, x = a and x = 2a. If the potential energy of the system is zero, then Q:q is
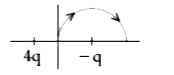
View SolutionA two point charges 4q and -q are fixed on the x - axis x=−d2andx=d2 , respectively. If a third point charge 'q' is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionAlong the x-axis, three charges q2,−q and q2 are placed at x=0,x=a and x=2a respectively. The resultant electric potential at a point P located at a distance r from the charge −q, (r>>a) is : ( ε0 is the permittivity of free space)
View SolutionFour charges Q1,Q2,Q3 and Q4 of same magnitude are fixed along the x axis at x=−2a,−a,+a and +2a, respectively. A positive charge q is placed on the positive y axis at a distance b>0. Four options of the signs of these charges are given in List I. The direction of the forces on the charge q is given in List II. Match List I with List II and select the correct answer using the code given below the lists.

List-IList-II(P)Q1,Q2,Q3,Q4all positive(1)+x(Q)Q1,Q2 positive, Q3,Q4 negative(2)−x(R)Q1,Q4 positive ,Q2,Q3 negative(3)+y(S)Q1,Q3 positive , Q2,Q4 negative(4)−y
View SolutionTwo point charges (+Q) and (−2Q) are fixed on the X-axis at positions a and 2a from origin respectively. At what positions on the axis, the resultant electric field is zero
View Solution
