A parallel plate capacitor having a plate separation of 2mm is charged by connecting it to a 300v supply. The energy density is
0.01j/m2
0.01j/m3
0.1j/m3
10j/m3
The correct Answer is:B
To find the energy density of a parallel plate capacitor, we can follow these steps:
Step 1: Understand the formula for energy density
The energy density (u) in a capacitor is given by the formula:
u=12ϵE2
where:
- ϵ is the permittivity of free space (ϵ0≈8.854×10−12F/m)
- E is the electric field between the plates.
Step 2: Relate electric field to voltage and distance
The electric field (E) between the plates of a capacitor can be expressed as:
E=Vd
where:
- V is the voltage across the plates (300 V in this case)
- d is the separation between the plates (2 mm = 2×10−3 m).
Step 3: Substitute E into the energy density formula
Substituting E into the energy density formula, we get:
u=12ϵ(Vd)2
Step 4: Plug in the values
Now we can substitute the known values into the equation:
- ϵ=8.854×10−12F/m
- V=300V
- d=2×10−3m
Thus, we have:
u=12×8.854×10−12×(3002×10−3)2
Step 5: Calculate the electric field
Calculating the electric field:
E=3002×10−3=150000V/m
Step 6: Substitute E back into the energy density formula
Now substituting E back into the energy density formula:
u=12×8.854×10−12×(150000)2
Step 7: Calculate the energy density
Calculating (150000)2:
(150000)2=22500000000V2/m2
Now substituting this value into the energy density equation:
u=12×8.854×10−12×22500000000
u=12×8.854×10−12×2.25×1010
u=0.0997J/m3≈0.1J/m3
Final Answer
The energy density is approximately:
u≈0.1J/m3
The energy density (u) in a capacitor is given by the formula:
u=12ϵE2
where:
- ϵ is the permittivity of free space (ϵ0≈8.854×10−12F/m)
- E is the electric field between the plates.
The electric field (E) between the plates of a capacitor can be expressed as:
E=Vd
where:
- V is the voltage across the plates (300 V in this case)
- d is the separation between the plates (2 mm = 2×10−3 m).
Substituting E into the energy density formula, we get:
u=12ϵ(Vd)2
Now we can substitute the known values into the equation:
- ϵ=8.854×10−12F/m
- V=300V
- d=2×10−3m
u=12×8.854×10−12×(3002×10−3)2
Calculating the electric field:
E=3002×10−3=150000V/m
Now substituting E back into the energy density formula:
u=12×8.854×10−12×(150000)2
Calculating (150000)2:
(150000)2=22500000000V2/m2
u=12×8.854×10−12×22500000000
u=12×8.854×10−12×2.25×1010
u=0.0997J/m3≈0.1J/m3
The energy density is approximately:
u≈0.1J/m3
Similar Questions
The plates of a parallel plate capacitor have an area of 90cm2 and each are separated by 2mm. The capacitor is charged by connecting it to a 400 V supply. Then the energy density of the energy stored (in Jm−3) in the capacitor is (take ε0=8.8×10−12Fm−1)
View SolutionA 5.80μF parallel-plate air capacitor has a plate separation of 5.00mm and is charged to a potential difference of 400V. Calculate the energy density in the region between the plates, in Jm3
View SolutionConsider a parallel plate capacitor having charge Q. Then,
View SolutionA parallel plate capacitor is charged. If the plates are pulled apart
View SolutionA parallel plate capacitor of area 100cm2 and plate separation 8.85 mm is charged to a potential difference of 100 V when air is used between the plates. The capacitor is now isolated and air is replaced by glass (εr−5), then:
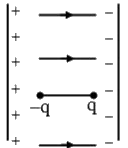
View SolutionAn electric dipole of dipole moment 2×10−10 coulomb is placed between parallel plate capacitor (see figure) having plate separation 2 cm and charged upto 100 V. Potential energy of the dipole will be -
View SolutionA pararllel plate capacitor has plates of area A and separation d and is charged to potential diference V. The charging battery is then disconnected and the plates are pulle apart until their separation is 2d. What is the work required to separate the plates?
View SolutionA parallel -plate capacitor having plate area 25cm^2 and separation 1 mm is connected to a battery of 6 V.. Calculate the charge flowing through the battery . How much work has been done by the battery during the process ?
View SolutionA parallel-plate capacitor having plate are 100cm2 and separation 1.0 mm holds a charge of 0.12μC when connected to a 120 V battery. Find the dielectric constant of the material filling the gap.
View SolutionA parallel plate capacitor of plate separation 2mm is connected in an electric circuit having source voltage 400V. If the plate area is 60cm2, then the value of displacement current for 10−6sec will be
View Solution
