The two metallic plates of radius are placed at a distance apart and its capacity is . If a plate of radius and thickness of dielectric constant is placed between the plates of the condenser, then its capacity will be
7C/2
3C/7
7C/3
9C/4
The correct Answer is:D
To solve the problem step by step, we need to analyze the situation where a dielectric slab is inserted between the plates of a capacitor. We will find the new capacitance after inserting the dielectric.
Step 1: Understand the initial capacitance
The initial capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- d is the distance between the plates.
For plates of radius r, the area A is:
A=πr2
Thus, the initial capacitance can be expressed as:
C=ε0πr2d
Step 2: Calculate the capacitance of the smaller capacitor with dielectric
When a dielectric slab of radius r2 and thickness d with dielectric constant K=6 is inserted, we need to calculate the capacitance of this smaller capacitor C1.
The area of the smaller plate is:
A1=π(r2)2=πr24
The capacitance C1 of this smaller capacitor with the dielectric is:
C1=Kε0A1d=6ε0(πr24)d=3πr2ε02d
Since C=ε0πr2d, we can express C1 in terms of C:
C1=32C
Step 3: Calculate the capacitance of the remaining area
The remaining area A2 of the capacitor (the area not covered by the dielectric) is:
A2=πr2−A1=πr2−πr24=3πr24
The capacitance C2 of this remaining area without the dielectric is:
C2=ε0A2d=ε0(3πr24)d=3πr2ε04d
Again, expressing C2 in terms of C:
C2=34C
Step 4: Combine the capacitances
Since C1 and C2 are in parallel, the total capacitance C′ is given by:
C′=C1+C2=32C+34C
To combine these fractions, we find a common denominator:
C′=64C+34C=94C
Final Answer
Thus, the new capacitance after inserting the dielectric slab is:
C′=94C
The initial capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- d is the distance between the plates.
A=πr2
Thus, the initial capacitance can be expressed as:
C=ε0πr2d
When a dielectric slab of radius r2 and thickness d with dielectric constant K=6 is inserted, we need to calculate the capacitance of this smaller capacitor C1.
A1=π(r2)2=πr24
The capacitance C1 of this smaller capacitor with the dielectric is:
C1=Kε0A1d=6ε0(πr24)d=3πr2ε02d
Since C=ε0πr2d, we can express C1 in terms of C:
C1=32C
The remaining area A2 of the capacitor (the area not covered by the dielectric) is:
A2=πr2−A1=πr2−πr24=3πr24
The capacitance C2 of this remaining area without the dielectric is:
C2=ε0A2d=ε0(3πr24)d=3πr2ε04d
Again, expressing C2 in terms of C:
C2=34C
Since C1 and C2 are in parallel, the total capacitance C′ is given by:
C′=C1+C2=32C+34C
To combine these fractions, we find a common denominator:
C′=64C+34C=94C
Thus, the new capacitance after inserting the dielectric slab is:
C′=94C
Similar Questions
Knowledge Check
A capacitor is made of two circular plates of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
A√mgdπε0r2B√mgdπε0rC√mgd2πε0r2D√mgdπε0r2
A parallel plate capacitor each with plate area A and separation ‘d’ is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change if any, will take place in
(i) charge on the plates
(ii) electric field intensity between the plates,
(iii) capacitance of the capacitor
Justify your answer in each case
View SolutionA parallel plate condenser with oil (dielectric constant 2) between the plates has capacitance C. If oil is removed, the capacitance of capacitor becomes
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionFigue shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab is
View SolutionFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the gaps between the plates and the electric slab will be
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

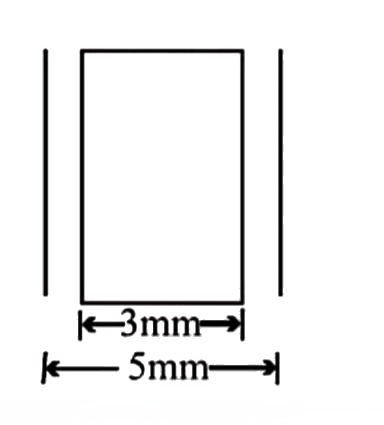
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View Solution
