A condenser having a capacity of is charged to and is then joined to an uncharged condenser of and then removed. The ratio of the charges on and and the potential of will be
The correct Answer is:C
To solve the problem step by step, we will follow the principles of capacitors, charge conservation, and voltage relationships.
Step 1: Calculate the initial charge on the 6 µF capacitor
The charge Q1 on the 6 µF capacitor when it is charged to 100 V can be calculated using the formula:
Q=C⋅V
Substituting the values:
Q1=6×10−6F×100V=600×10−6C=600μC
Step 2: Set up the equations for the connected capacitors
When the charged capacitor is connected to the uncharged 14 µF capacitor, the total charge is conserved. Let Q2 be the charge on the 14 µF capacitor after they are connected. The total charge before they are connected is:
Qtotal=Q1+Q2
Since the 14 µF capacitor is initially uncharged, we have:
Qtotal=Q1=600μC
Step 3: Relate the charges and voltages after connection
After connecting the two capacitors, they will reach a common voltage Vc. The relationship between charge, capacitance, and voltage gives us:
Q1=C1⋅VcandQ2=C2⋅Vc
This leads to:
Q1=6×10−6⋅VcandQ2=14×10−6⋅Vc
Step 4: Write the conservation of charge equation
From charge conservation, we have:
Q1+Q2=600×10−6
Substituting the expressions for Q1 and Q2:
6×10−6⋅Vc+14×10−6⋅Vc=600×10−6
Factoring out Vc:
(6+14)×10−6⋅Vc=600×10−6
20×10−6⋅Vc=600×10−6
Solving for Vc:
Vc=600×10−620×10−6=30V
Step 5: Calculate the charges on each capacitor
Now we can find Q1 and Q2 using the common voltage:
Q1=6×10−6⋅30=180×10−6C=180μC
Q2=14×10−6⋅30=420×10−6C=420μC
Step 6: Find the ratio of the charges
The ratio of the charges on the 6 µF and 14 µF capacitors is:
Ratio=Q1Q2=180μC420μC=180420=37
Final Results
- The ratio of the charges Q1:Q2=3:7
- The potential of the 6 µF capacitor V1=30V
The charge Q1 on the 6 µF capacitor when it is charged to 100 V can be calculated using the formula:
Q=C⋅V
Substituting the values:
Q1=6×10−6F×100V=600×10−6C=600μC
When the charged capacitor is connected to the uncharged 14 µF capacitor, the total charge is conserved. Let Q2 be the charge on the 14 µF capacitor after they are connected. The total charge before they are connected is:
Qtotal=Q1+Q2
Since the 14 µF capacitor is initially uncharged, we have:
Qtotal=Q1=600μC
After connecting the two capacitors, they will reach a common voltage Vc. The relationship between charge, capacitance, and voltage gives us:
Q1=C1⋅VcandQ2=C2⋅Vc
This leads to:
Q1=6×10−6⋅VcandQ2=14×10−6⋅Vc
From charge conservation, we have:
Q1+Q2=600×10−6
Substituting the expressions for Q1 and Q2:
6×10−6⋅Vc+14×10−6⋅Vc=600×10−6
Factoring out Vc:
(6+14)×10−6⋅Vc=600×10−6
20×10−6⋅Vc=600×10−6
Solving for Vc:
Vc=600×10−620×10−6=30V
Now we can find Q1 and Q2 using the common voltage:
Q1=6×10−6⋅30=180×10−6C=180μC
Q2=14×10−6⋅30=420×10−6C=420μC
The ratio of the charges on the 6 µF and 14 µF capacitors is:
Ratio=Q1Q2=180μC420μC=180420=37
- The ratio of the charges Q1:Q2=3:7
- The potential of the 6 µF capacitor V1=30V
Similar Questions
Find the charges on 6μF and 4μF capacitors
View SolutionA capacitor having capacity of 2μF is charged to 200V and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
View SolutionA condenser of capacitance 10μF has been charged to 100V. It is now connected to another uncharged condenser in parallel. The common potential becomes 40V. The capacitance of another condenser is
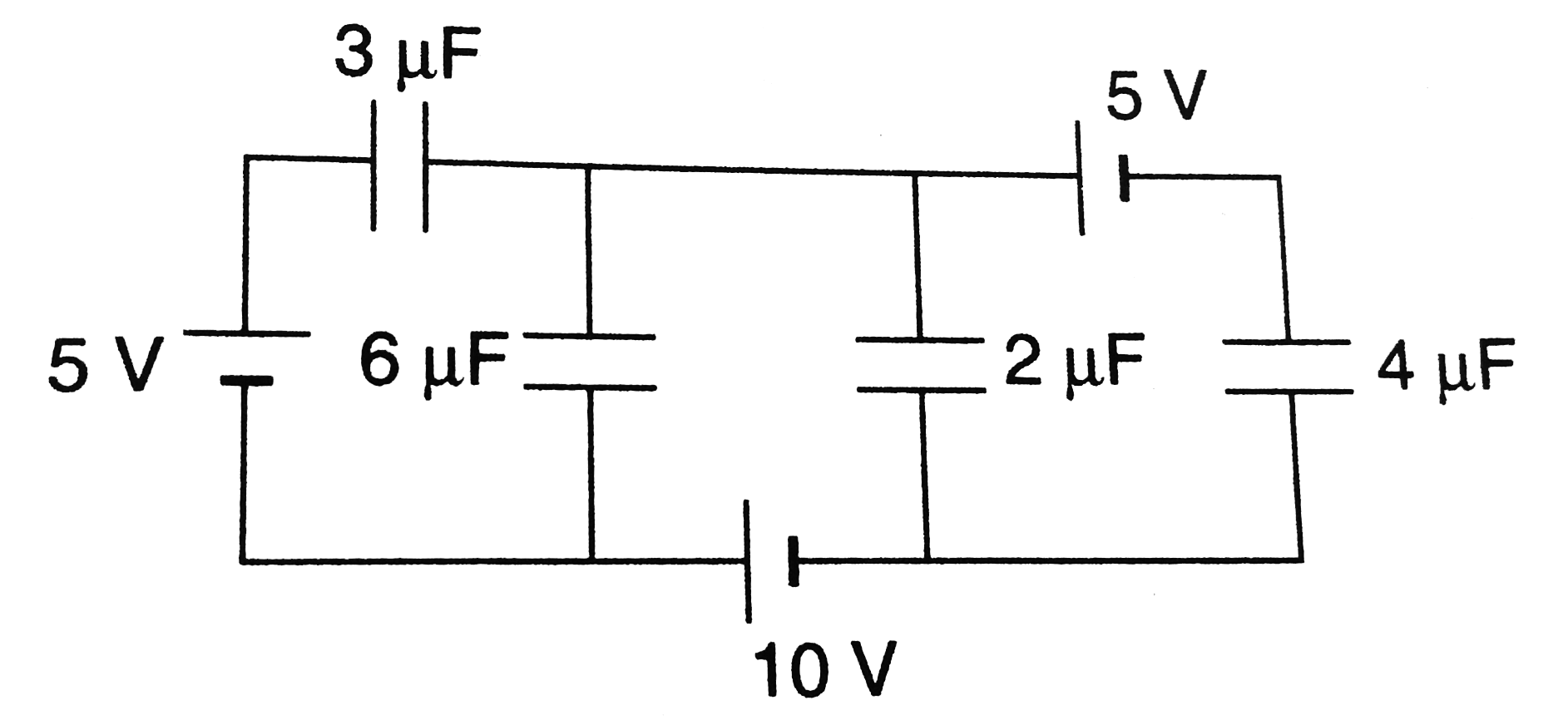
View SolutionIn the circuit shown in figure, the ratio of charge on 5μF and 2μF capacitor is
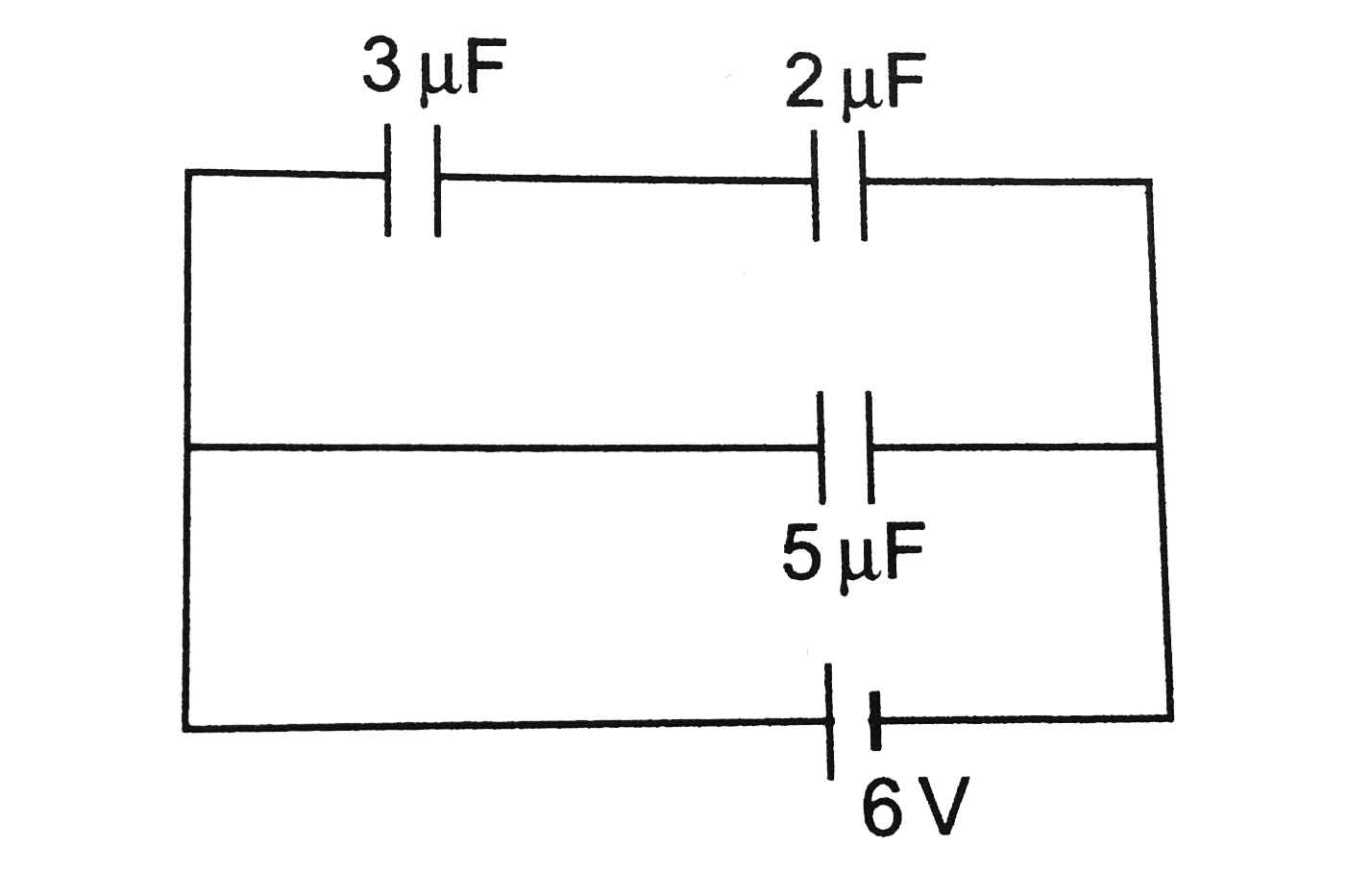
View SolutionThe charge on 3μF capacitor shown in the figure is
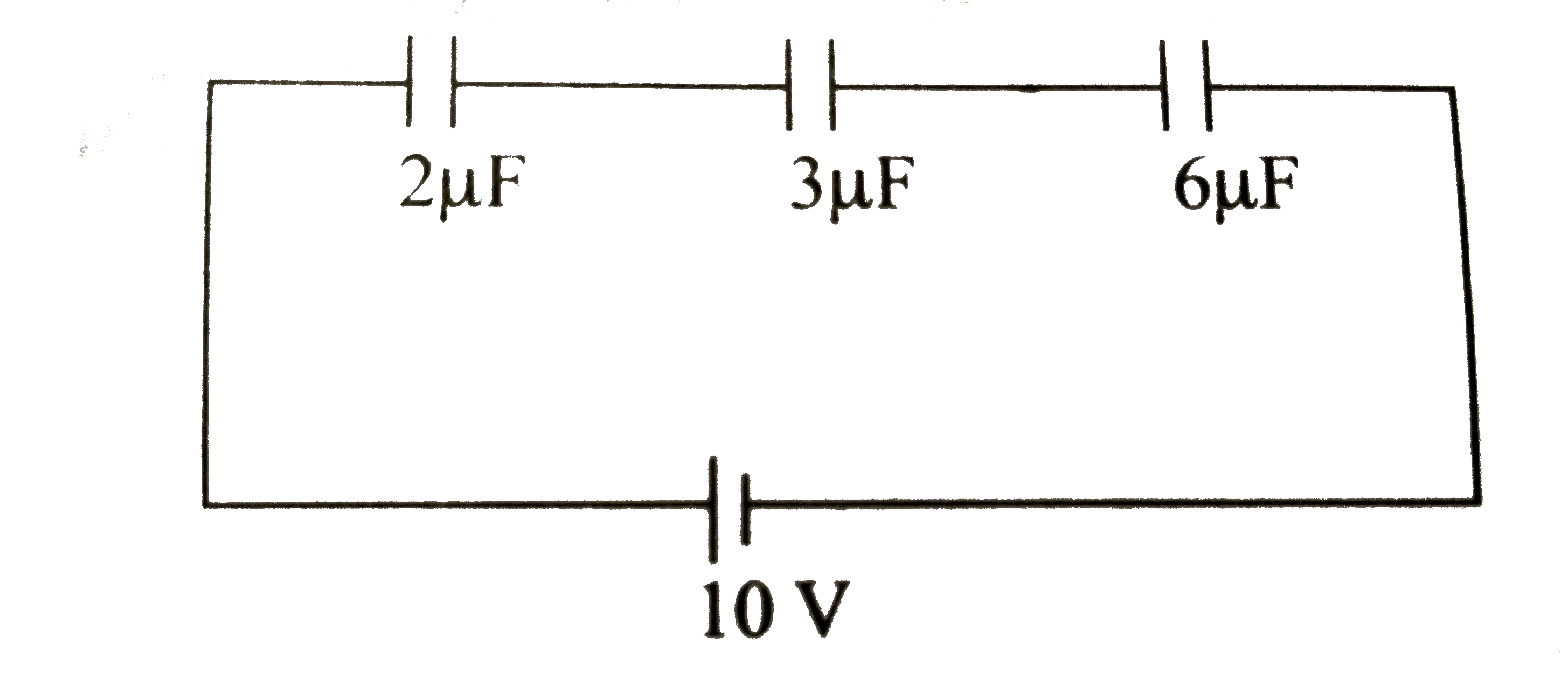
View SolutionThe charge on the 4μF capacitor in the steady state is
View SolutionA capacitor of 20μF charged upto 500 V is connected in parallel with another capacitor of 10μF, which is charged upto 200 V. the common potential is
View SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
View SolutionIf the potential of a capacitor having capacity of 6μF is increased from 10 V to 20 V,then increase in its energy will be
View SolutionThe ratio of potential differences between 1μFand5μF capacitors is
View Solution