An ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
both A and V will increase
both A and V will decrease
A will decrease and V will increase
A will increase and V will decrease
The correct Answer is:D
To solve the problem step-by-step, we will analyze the circuit with the ammeter, voltmeter, and the additional resistance connected in parallel with the voltmeter.
Step 1: Understand the initial circuit
Initially, we have an ammeter (A) and a voltmeter (V) connected in series to an electric cell with negligible internal resistance. The resistance of both the ammeter and voltmeter is given as R.
Step 2: Determine the current through the circuit
The reading of the ammeter is A. Therefore, the current flowing through the circuit is:
I=A
Step 3: Calculate the voltage across the voltmeter
The voltage across the voltmeter can be expressed using Ohm's law:
V=I×R
Substituting the value of I:
V=A×R(Equation 1)
Step 4: Analyze the total resistance in the circuit
The total resistance in the circuit (since the ammeter and voltmeter are in series) is:
Rtotal=R+R=2R
The emf of the cell can be expressed as:
V′=I×Rtotal=A×2R(Equation 2)
Step 5: Introduce the new resistance in parallel with the voltmeter
When another resistance R is connected in parallel with the voltmeter, the effective resistance Reff of the voltmeter and the new resistance in parallel can be calculated as:
Reff=R×RR+R=R22R=R2
Step 6: Calculate the new total resistance
Now, the new total resistance in the circuit becomes:
Rnew=R+Reff=R+R2=3R2
Step 7: Calculate the new current in the circuit
Using Ohm's law, the new current I′ in the circuit can be calculated as:
I′=V′Rnew=V′3R2=2V′3R
Substituting V′=2AR from Equation 2:
I′=2×2AR3R=4A3(Equation 3)
Step 8: Calculate the new reading of the voltmeter
The new reading of the voltmeter G can be calculated using the effective resistance:
G=I′×Reff=(4A3)×R2=4AR6=2V3(Equation 4)
Step 9: Conclusion
From the calculations, we have:
- The new current I′=4A3 (which is greater than A)
- The new voltmeter reading G=2V3 (which is less than V)
Summary of Results
- The ammeter reading increases: A′=4A3
- The voltmeter reading decreases: G=2V3
Final Answer
The correct conclusion is that the ammeter reading increases while the voltmeter reading decreases.
Initially, we have an ammeter (A) and a voltmeter (V) connected in series to an electric cell with negligible internal resistance. The resistance of both the ammeter and voltmeter is given as R.
The reading of the ammeter is A. Therefore, the current flowing through the circuit is:
I=A
The voltage across the voltmeter can be expressed using Ohm's law:
V=I×R
Substituting the value of I:
V=A×R(Equation 1)
The total resistance in the circuit (since the ammeter and voltmeter are in series) is:
Rtotal=R+R=2R
The emf of the cell can be expressed as:
V′=I×Rtotal=A×2R(Equation 2)
When another resistance R is connected in parallel with the voltmeter, the effective resistance Reff of the voltmeter and the new resistance in parallel can be calculated as:
Reff=R×RR+R=R22R=R2
Now, the new total resistance in the circuit becomes:
Rnew=R+Reff=R+R2=3R2
Using Ohm's law, the new current I′ in the circuit can be calculated as:
I′=V′Rnew=V′3R2=2V′3R
Substituting V′=2AR from Equation 2:
I′=2×2AR3R=4A3(Equation 3)
The new reading of the voltmeter G can be calculated using the effective resistance:
G=I′×Reff=(4A3)×R2=4AR6=2V3(Equation 4)
From the calculations, we have:
- The new current I′=4A3 (which is greater than A)
- The new voltmeter reading G=2V3 (which is less than V)
- The ammeter reading increases: A′=4A3
- The voltmeter reading decreases: G=2V3
The correct conclusion is that the ammeter reading increases while the voltmeter reading decreases.
Similar Questions
An ammeter and a voltmeter are joined in sereis to a cell. Their readings are A and V respectively. If a resistance is now joinding parallel with the voltmeter. Then
View SolutionAn ammeter and a voltmeter are joined in series to a cell. Their readings are A and V respectively. If a resistance is now joining parallel with the voltmeter. Then
View SolutionA voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find the ratio of R1 and R2.
View SolutionAn ammeter, voltmeter and a resistor are connected in series to a cell and the readings are noted as I and V. If another resistor R is connected in parallel with a voltmeter, then
View SolutionAn ammeter and a voltmeter are connected in series to an ideal battery of emf E. If the ammeter reads I and voltmeter reading V, then
View SolutionIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmeter, also of resistance R, is connected across Y.
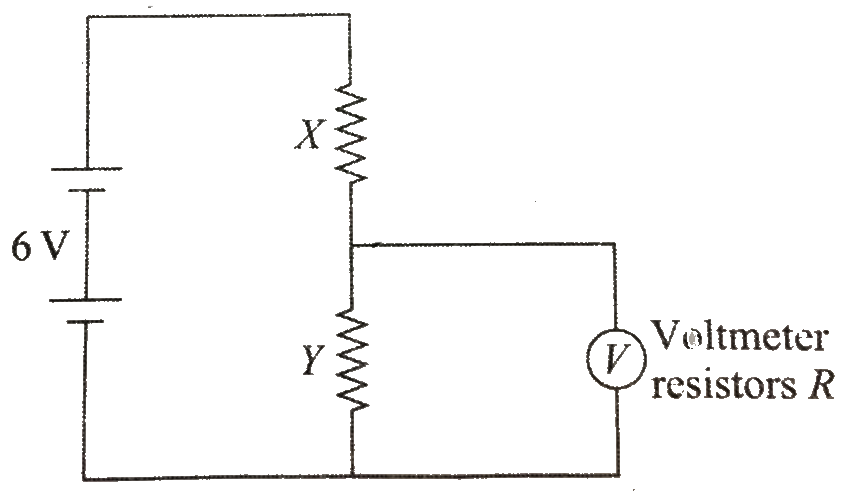
What is the reading of the voltmeter?
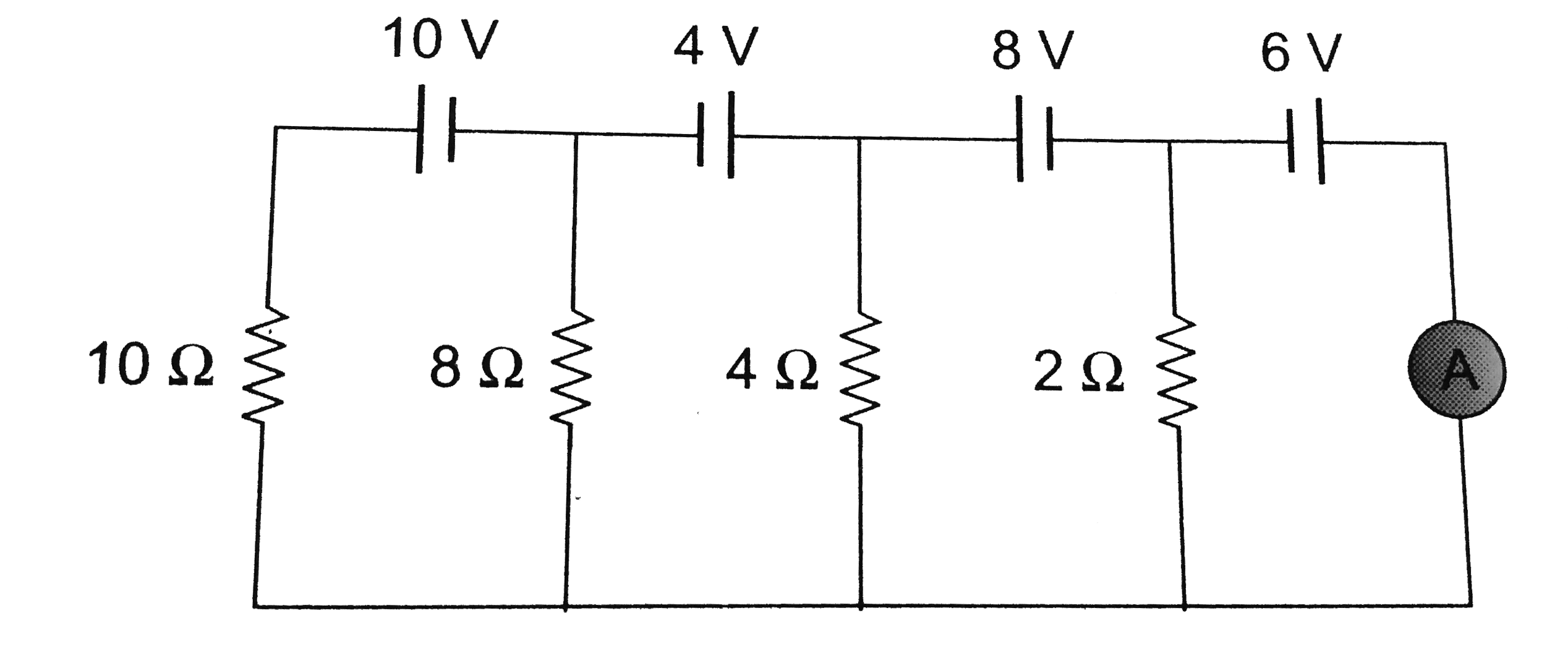
View SolutionFind the reading of the ideal ammeter connected in the given circuit. Assume that the cells have negligible internal resistance.
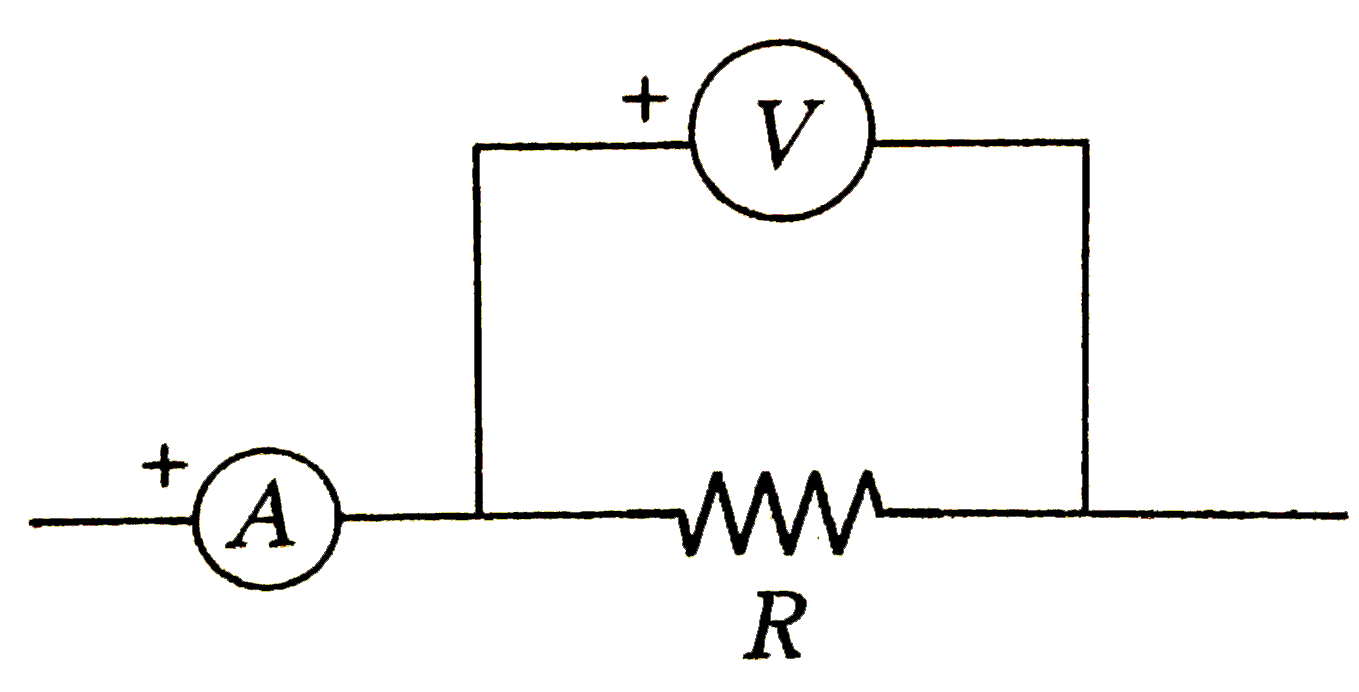
View SolutionAn ammeter A, a voltmeter V and a resistance R are connected as shown in the figure. If the voltmeter reading is 1.6V and the ammeter reading is 0.4A, then R is
View SolutionA voltmeter of resistance 600Ω when connected in turn across resistances R1 and R2 gives readings of V1 and V2, respectively. If the battery is ideal, then

View SolutionAn ammeter and a voltmeter are connected in series to a battery with an emf ξ=6.0V. When a certain resistance is connected in parallel with the voltmeter, the readings of the latter decreases η=2.0 times, whereas the readings of the ammeter increase the same number of times, Find the voltmeter readings after the connection of the resistance.
View Solution
