A cell of itnernal resitance 1.5Ω and of e.m.f. 1.5 volt balances 500cm on a potentiomter wire. If a wirr of 15 Ω is connected between the balance point and the cell, then tha balance point will shift
To zero
By 500 cm
By 750 cm
None of the above
The correct Answer is:D
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the Initial Conditions
We have a cell with:
- Internal resistance (R_internal) = 1.5 Ω
- Electromotive force (e.m.f) = 1.5 V
- Initial balance point on the potentiometer wire = 500 cm
Step 2: Analyze the Effect of Adding a Resistor
When a wire of resistance 15 Ω is connected between the balance point and the cell, we need to determine how this affects the balance point.
Step 3: Calculate the Total Resistance
The total resistance in the circuit when the 15 Ω wire is connected becomes:
- Total Resistance (R_total) = R_internal + R_additional
- R_total = 1.5 Ω + 15 Ω = 16.5 Ω
Step 4: Calculate the Current in the Circuit
Using Ohm's Law (V = IR), we can find the current (I) flowing through the circuit:
- I = e.m.f / R_total
- I = 1.5 V / 16.5 Ω
- I ≈ 0.0909 A
Step 5: Determine the New Balance Point
The potential drop across the 15 Ω wire can be calculated using Ohm's Law:
- V_drop = I * R_additional
- V_drop = 0.0909 A * 15 Ω
- V_drop ≈ 1.3635 V
Step 6: Compare the Potential Drops
The initial potential drop across the potentiometer wire was:
- V_initial = e.m.f = 1.5 V
With the additional resistance, the potential drop across the potentiometer wire will now be:
- V_new = V_initial - V_drop
- V_new = 1.5 V - 1.3635 V ≈ 0.1365 V
Step 7: Calculate the New Balance Point
Using the ratio of the potential drops, we can find the new balance point (L_new):
- L_new / 500 cm = V_new / V_initial
- L_new = 500 cm * (0.1365 V / 1.5 V)
- L_new ≈ 45.5 cm
Conclusion
The new balance point shifts to approximately 45.5 cm from the original balance point.
We have a cell with:
- Internal resistance (R_internal) = 1.5 Ω
- Electromotive force (e.m.f) = 1.5 V
- Initial balance point on the potentiometer wire = 500 cm
When a wire of resistance 15 Ω is connected between the balance point and the cell, we need to determine how this affects the balance point.
The total resistance in the circuit when the 15 Ω wire is connected becomes:
- Total Resistance (R_total) = R_internal + R_additional
- R_total = 1.5 Ω + 15 Ω = 16.5 Ω
Using Ohm's Law (V = IR), we can find the current (I) flowing through the circuit:
- I = e.m.f / R_total
- I = 1.5 V / 16.5 Ω
- I ≈ 0.0909 A
The potential drop across the 15 Ω wire can be calculated using Ohm's Law:
- V_drop = I * R_additional
- V_drop = 0.0909 A * 15 Ω
- V_drop ≈ 1.3635 V
The initial potential drop across the potentiometer wire was:
- V_initial = e.m.f = 1.5 V
- V_new = V_initial - V_drop
- V_new = 1.5 V - 1.3635 V ≈ 0.1365 V
Using the ratio of the potential drops, we can find the new balance point (L_new):
- L_new / 500 cm = V_new / V_initial
- L_new = 500 cm * (0.1365 V / 1.5 V)
- L_new ≈ 45.5 cm
The new balance point shifts to approximately 45.5 cm from the original balance point.
Similar Questions
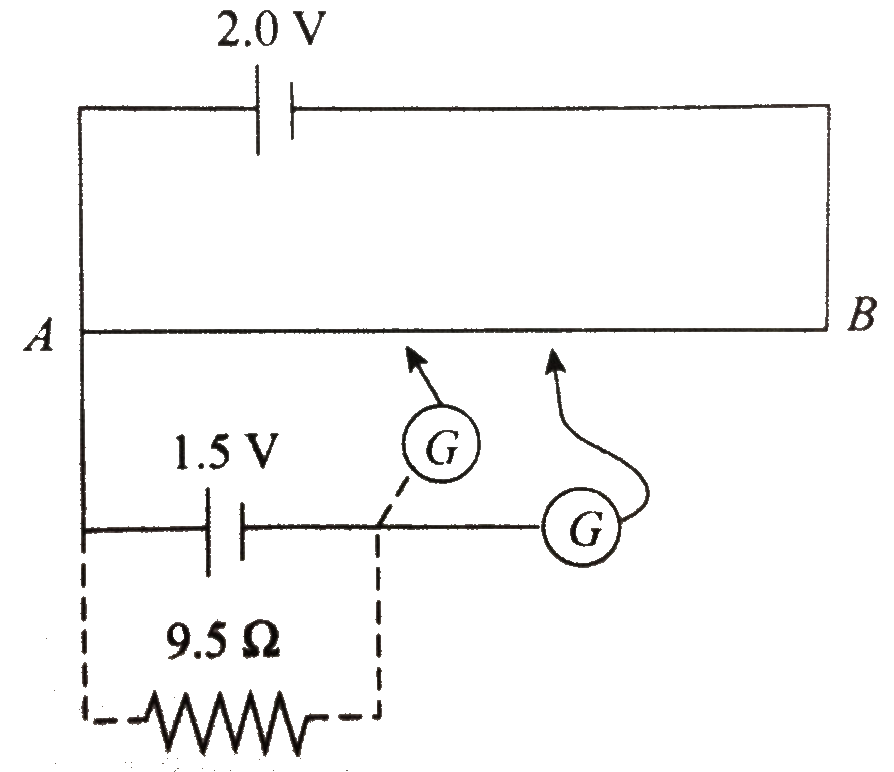
Figure 6.13 shows a 2.0V potentiometer used for the determination of internal resistance of a 1.5V cell. The balance point of the cell in open circuit is 76.3cm. Whan a resistor of 9.5Ω is used in the external circuit of the cell, the balance point shifts to 64.8cm, length of the potentiometer. Dentermine the internal resistance of the cell.
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View Solution
Knowledge Check
3V poteniometer used for the determination of internal resistance of a 2.4V cell. The balanced point of the cell in open circuit is 75.8cm. When a resistor of 10.2Ω is used in the external circuit of the cell the balance point shifts to 68.3cm length of the potentiometer wire. The internal resistance of the cell is
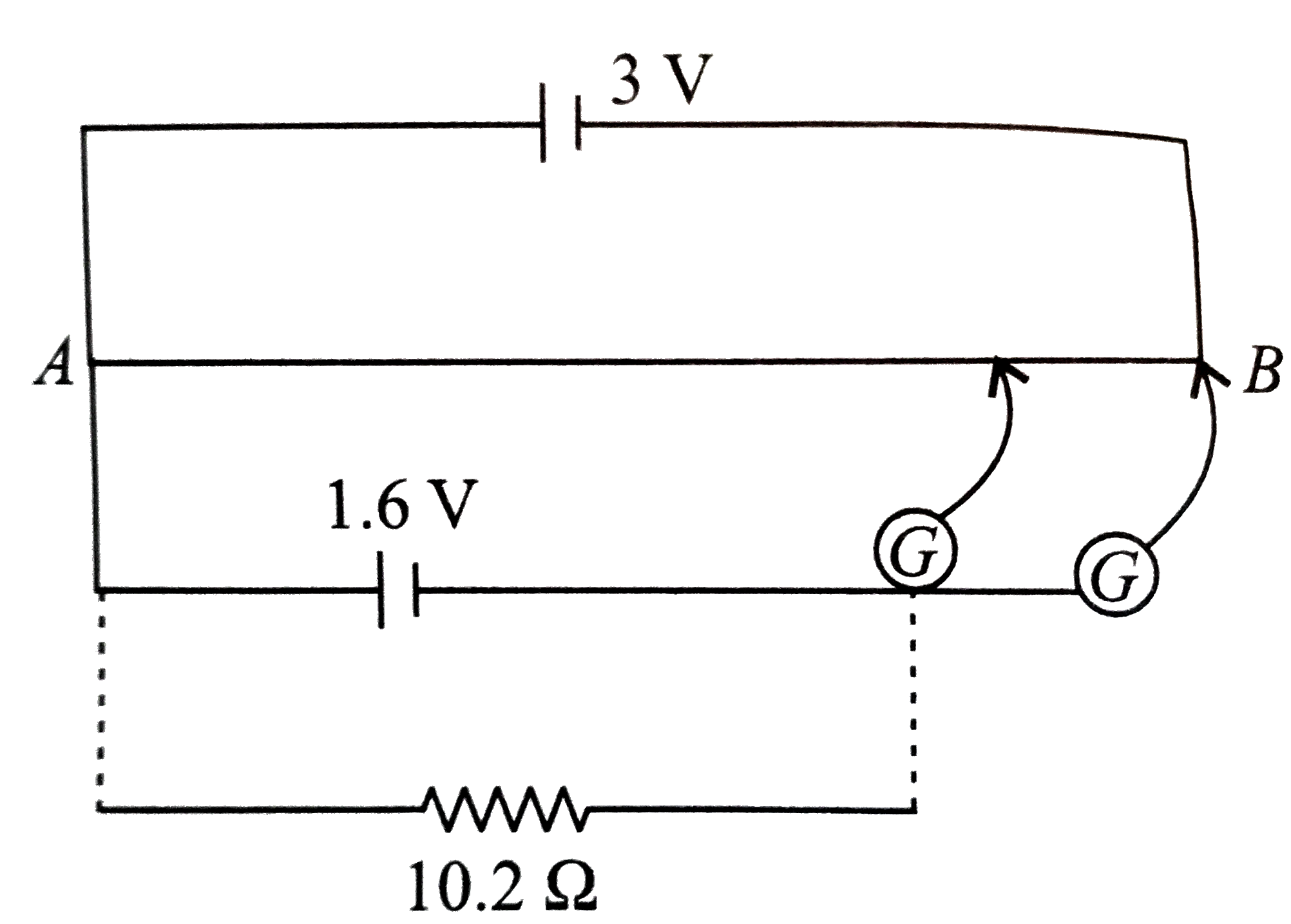 A2.5ΩB2.25ΩC1.12ΩD3.2Ω
A2.5ΩB2.25ΩC1.12ΩD3.2Ω
A 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionFor a cell of e.m.f. 2 V , a balance is obtained for 50 cm of the potentiometer wire. If the cell is shunted by a 2Ω resistor and the balance is obtained across 40 cm of the wire, then the internal resistance of the cell is
View SolutionStatement I: In the potentiometer circuit shown in figure. E1andE2 are the emf of cells C1andC2, repsectively, with E1>E2. Cell C1 has negligible internal resistance. For a given resistor R, the balance length is x. If the diameter of the potentiometer wire AB is increased, the balance length x will decrease.
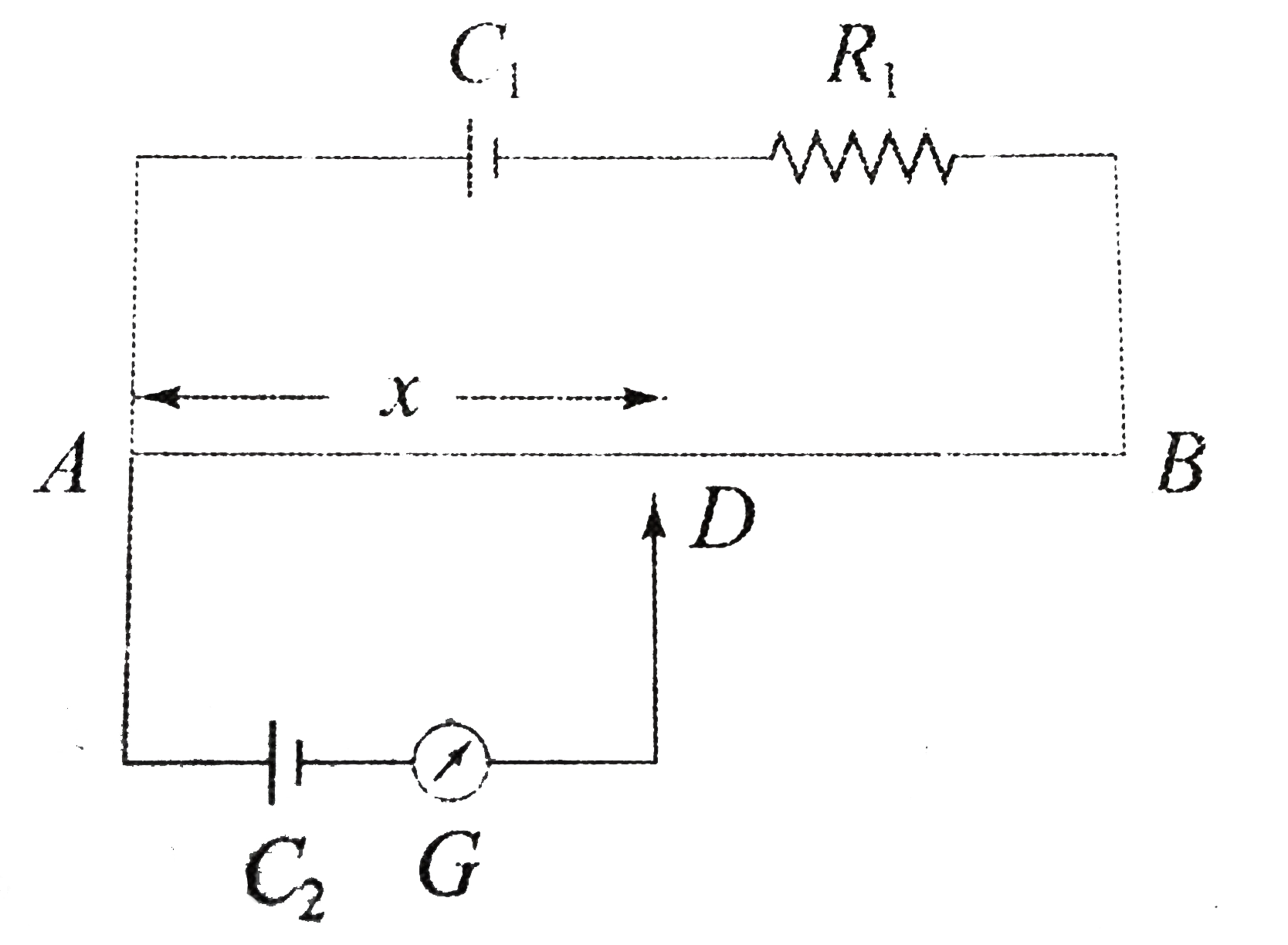
Statement II: At the balance point, the potential difference between AD due to cell C1isE2 , the emf of cell C2.
View SolutionA 5m potentiometer wire having 3Ω resistance per meter is connected to a storage cell of steady emf 2V and internal resistance 1Ω. A primary cell is balanced against 3.5m of it. When a resistance of 32/nΩ is put in series with the storage cell, the null point shifts to the centre of the last wire, i.e., 4.5m. What is 'n'?
View SolutionAn accumulator of emf 2V and negligible internal resistance is connected across a uniform wire of length 10 m and resistance 30Ω The appropriate terminals of a cell of emf 1.5V and internal resistance 1Ω is connected to one end of the wire and the other terminal of the cell is connected through a sensitive galvanometer to a slider on the wire. What is the length of the wire that will be required to produce zero deflection of the galvanometer? How will the balancing length change?
(a) When a coil of resistance 5Ω is placed in series with the accumulator.
(b) The cell of 1.5V is shunted with 5Ω resistor?
View Solution
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionIn a potentiometer arrangement, a cell of emf 1.5 V gives a balance point at 27 cm length of wire. If the cell is replaced by another cell and balance point shifts to 54 cm, the emf of the second cell is :
View Solution
