The e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
0.1ohm
1ohm
2ohm
0.5ohm
The correct Answer is:B
To find the internal resistance of the cell, we can use the information provided in the question and apply the relevant formula. Let's break down the solution step by step.
1. Identify the Given Values:
- Original length of the potentiometer wire (L1) = 150 cm
- Length of the wire when the shunt is connected (L2) = 100 cm
- Resistance of the shunt (R) = 2 Ω
2. Understand the Relationship:
- The internal resistance (r) of the cell can be calculated using the formula:
r=L1−L2L2×R
- Here, L1−L2 represents the change in length of the potentiometer wire when the shunt is connected.
3. Substitute the Values into the Formula:
- Calculate L1−L2:
L1−L2=150cm−100cm=50cm
- Now substitute the values into the formula:
r=50cm100cm×2Ω
4. Simplify the Expression:
- The fraction 50100 simplifies to 12:
r=12×2Ω=1Ω
5. Conclusion:
- The internal resistance of the cell is:
r=1Ω
Final Answer:
The internal resistance of the cell is 1 Ω.
---
- Original length of the potentiometer wire (L1) = 150 cm
- Length of the wire when the shunt is connected (L2) = 100 cm
- Resistance of the shunt (R) = 2 Ω
- The internal resistance (r) of the cell can be calculated using the formula:
r=L1−L2L2×R
- Here, L1−L2 represents the change in length of the potentiometer wire when the shunt is connected.
- Calculate L1−L2:
L1−L2=150cm−100cm=50cm
- Now substitute the values into the formula:
r=50cm100cm×2Ω
- The fraction 50100 simplifies to 12:
r=12×2Ω=1Ω
- The internal resistance of the cell is:
r=1Ω
The internal resistance of the cell is 1 Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-D
9 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
A Daniel cell is balanced on 125cm length of a potentiometer wire. Now the cells is short-circuited by a resistance 2ohm and the balance is obtained at 100cm. The internal resistance of the Dainel cell is
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
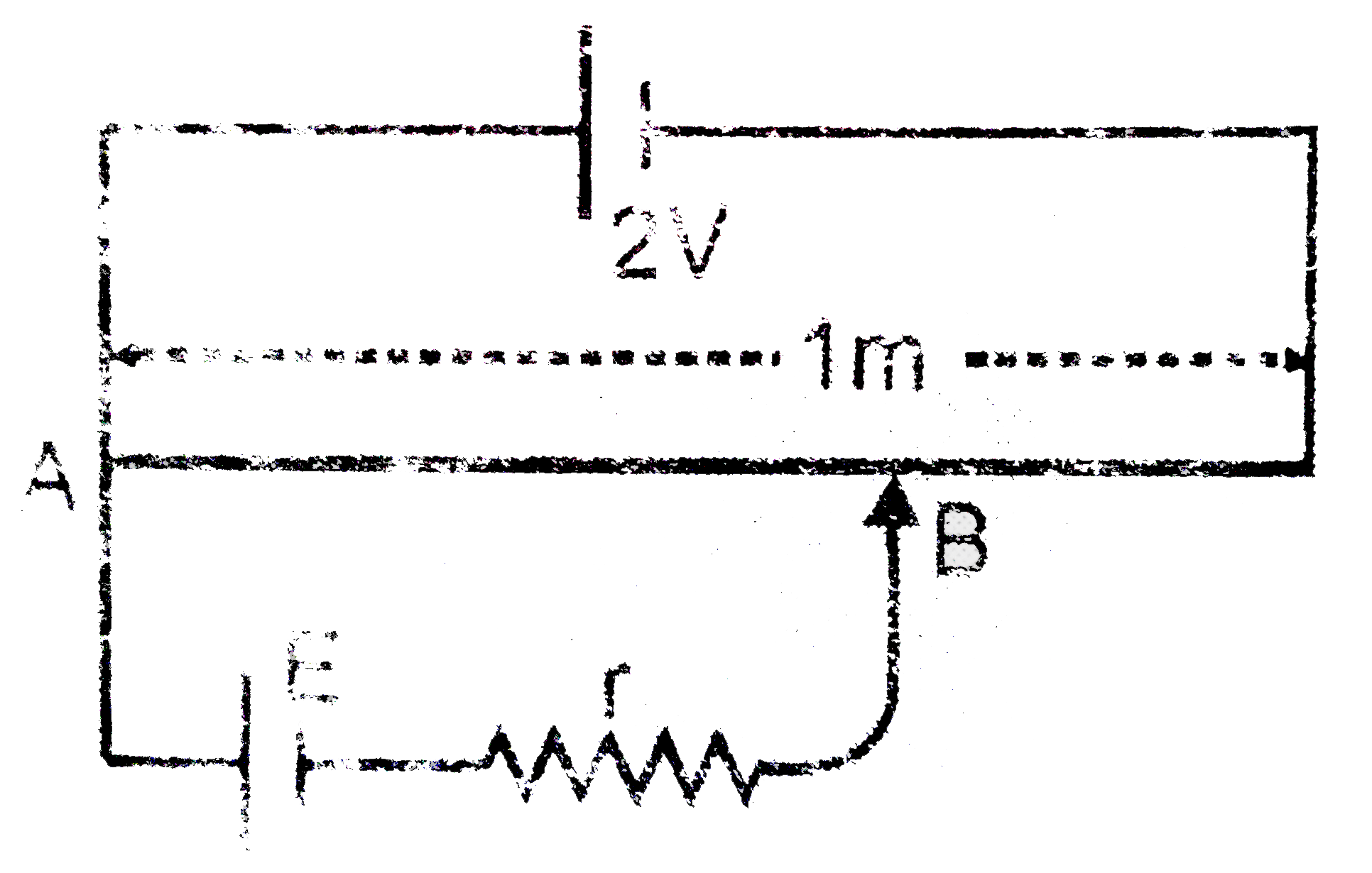
View SolutionIn a potentiometer arrangement for determining the emf of cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9Ω is used in the external circuit of cell , the balance point shifts to 300 cm. Determine the internal resistance of the cell.
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionFor a cell of e.m.f. 2 V , a balance is obtained for 50 cm of the potentiometer wire. If the cell is shunted by a 2Ω resistor and the balance is obtained across 40 cm of the wire, then the internal resistance of the cell is
View SolutionIn a potentiometer experiment it is found that no current passes through the galvanometer when the terminals of the cell are connected across 0.52m of the potentiometer wire. If the cell is shunted by a resistance of 5Ω balance is obtained when the cell connected across0.4m of the wire. Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment it is found that no current passes through the galvanometer when the terminals of the cell are connected across 0.52m of the potentiometer wire. If the cell is shunted by a resistance of 5Ω balance is obtained when the cell connected across0.4m of the wire. Find the internal resistance of the cell.
View Solution
