For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
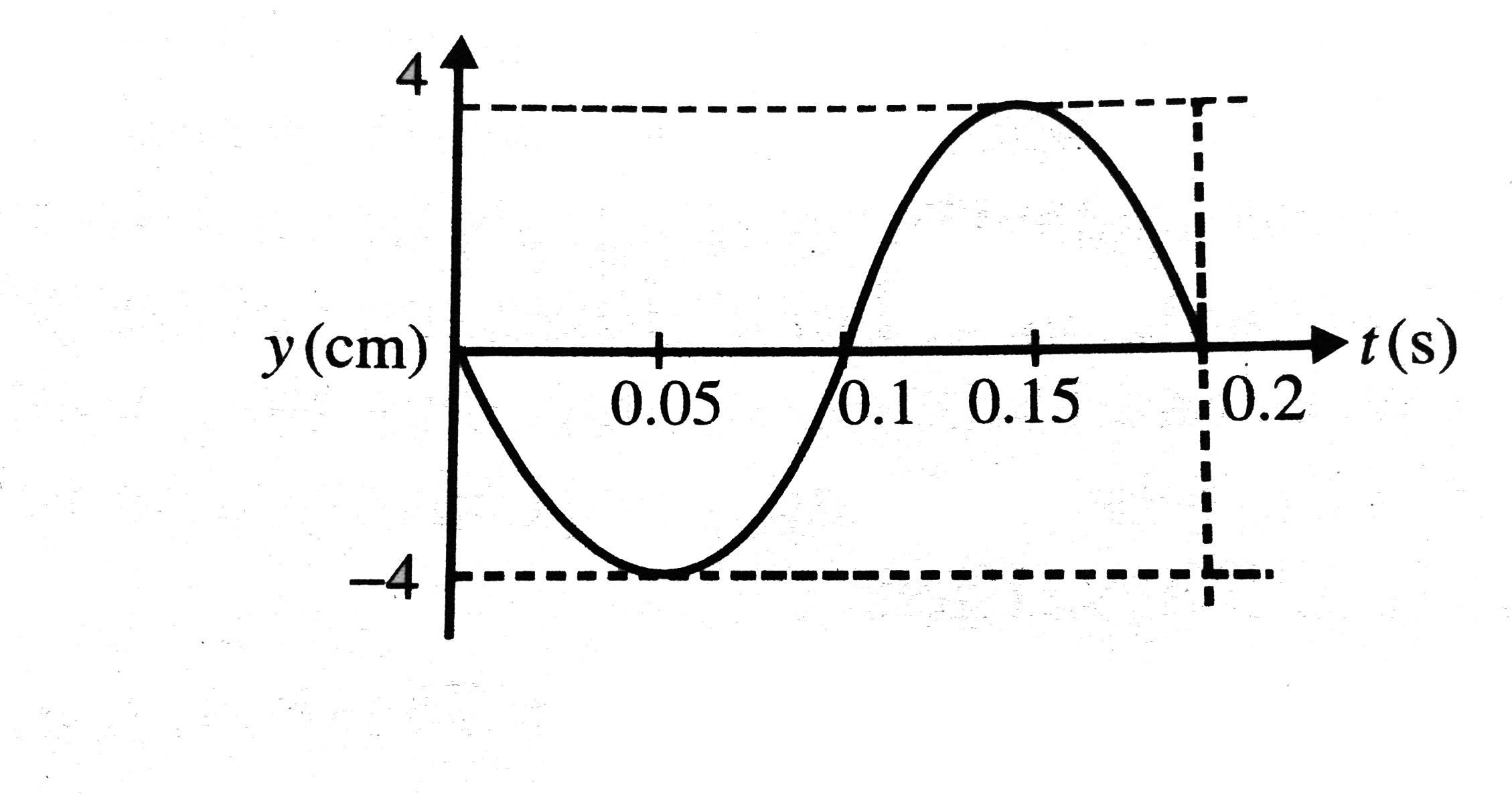
Transverse displacement of the particle at x = 0.05 m and t = 0.05 s is −2√2cm
Transverse displacement of the particle at x = 0.04 m and t = 0.025 s is −2√2cm
Speed of the travelling waves that interfere to produce this standing wave is 2m/s
The transverse velocity of the string particle at x=115m and t = 0.1 s is 20cm/s
The correct Answer is:A, C, D
Step by step video & image solution for For a certain transverse standing wave on a long string , an antinode is formed at x = 0 and next to it , a node is formed at x = 0.10 m , the displacement y(t)of the string particle at x = 0 is shown in Fig.7.97. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Fill in the Blanks Type34videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective Type2videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct Answer Type56videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
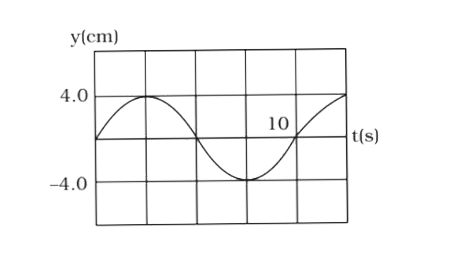
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?View SolutionA transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
 View Solution
View SolutionIn a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m.Then the wave length of the standing wave is
View SolutionThe wave funcation for a travelling wave on a string in given as
y(x,t)=(0.350m)sin(10πt−3πx+π4)
(a) What are the speed and direction of travel of the wave ?
(b) What is the vertical displacement of the string at t=0,x=0.1m ?View SolutionA wave of length 2m is superposed on its reflected wave to form a stationary wave. A node is located at x = 3m. The next node will be located at x=
View SolutionAdjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode.View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is y(x,t)=0.5sin(0.025πx)cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :
View Solution

