A standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
The energy density of a node is equal to energy density of an antinode for the first time at t=T/4
The energy density of node and antinode becomes equal after T/2 second
The displacement of the particle at antinode at t=T8 is √2A
The displacement of the particle at node is zero
The correct Answer is:C, D
To solve the problem of a standing wave in a string clamped between two rigid supports, we will analyze the situation step by step.
Step 1: Understand the standing wave equation
The displacement of a standing wave can be described by the equation:
y(x,t)=2Asin(kx)cos(ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency,
- t is time.
Step 2: Identify the parameters
Given that at t=0, the antinode is at its maximum displacement of 2A, we can deduce that:
- At t=0, cos(ωt)=1 (since cos(0)=1).
- Therefore, the displacement at the antinode is:
y(x,0)=2Asin(kx)
Step 3: Determine the position of the antinode
The antinodes occur where sin(kx)=1. This means:
kx=π2+nπ(n∈Z)
For the first antinode, we can take n=0:
kx=π2
Thus, the position of the first antinode is at:
x=π2k
Step 4: Analyze the displacement at t=T8
Now, we need to find the displacement at t=T8. The angular frequency ω is given by:
ω=2πT
Substituting t=T8 into the wave equation:
y(x,T8)=2Asin(kx)cos(2πT⋅T8)
This simplifies to:
y(x,T8)=2Asin(kx)cos(π4)
Since cos(π4)=1√2:
y(x,T8)=2Asin(kx)⋅1√2=2A√2sin(kx)=√2Asin(kx)
Step 5: Evaluate the displacement at the antinode
At the antinode (where sin(kx)=1):
y(x,T8)=√2A
Conclusion
Thus, the displacement of the particle at the antinode at t=T8 is:
y(x,T8)=√2A
Final Answer
The displacement of the particle at the antinode at t=T8 is √2A.
---
The displacement of a standing wave can be described by the equation:
y(x,t)=2Asin(kx)cos(ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency,
- t is time.
Given that at t=0, the antinode is at its maximum displacement of 2A, we can deduce that:
- At t=0, cos(ωt)=1 (since cos(0)=1).
- Therefore, the displacement at the antinode is:
y(x,0)=2Asin(kx)
The antinodes occur where sin(kx)=1. This means:
kx=π2+nπ(n∈Z)
For the first antinode, we can take n=0:
kx=π2
Thus, the position of the first antinode is at:
x=π2k
Now, we need to find the displacement at t=T8. The angular frequency ω is given by:
ω=2πT
Substituting t=T8 into the wave equation:
y(x,T8)=2Asin(kx)cos(2πT⋅T8)
This simplifies to:
y(x,T8)=2Asin(kx)cos(π4)
Since cos(π4)=1√2:
y(x,T8)=2Asin(kx)⋅1√2=2A√2sin(kx)=√2Asin(kx)
At the antinode (where sin(kx)=1):
y(x,T8)=√2A
Thus, the displacement of the particle at the antinode at t=T8 is:
y(x,T8)=√2A
The displacement of the particle at the antinode at t=T8 is √2A.
Topper's Solved these Questions
Similar Questions
A metal rod has length L, radius of its cross-section r. Youngs modulus Y and thermal coefficient of linear expansion is α.It is clamped between two rigid supports with negligible tension. If its temperature is increased by T∘C, then force exerted by the rod on any of the supports is
View SolutionA string is vibrating in its fifth overtone between two rigid supports 2.4 m apart. The distance between successive node and antinode is
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
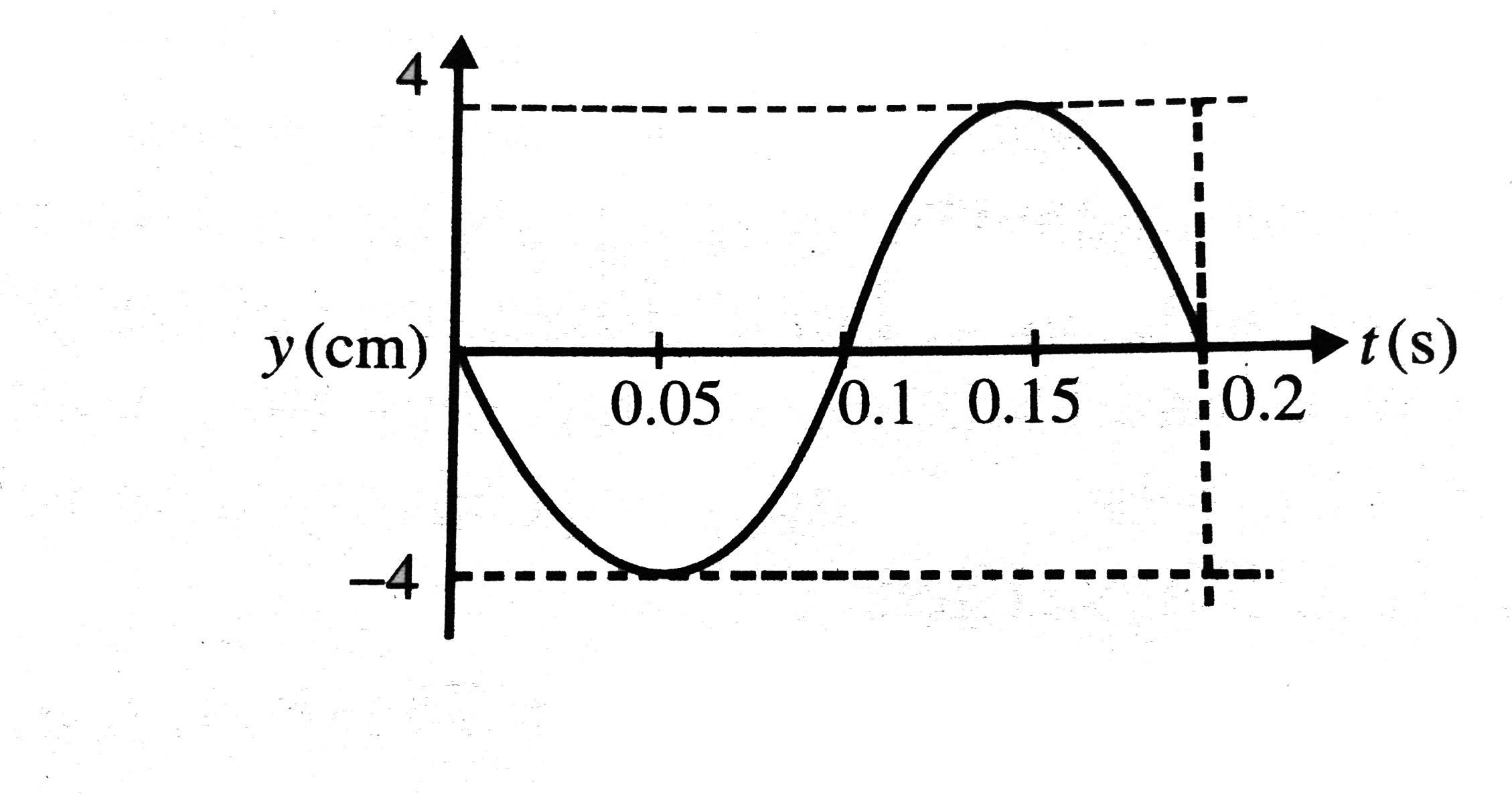 View Solution
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
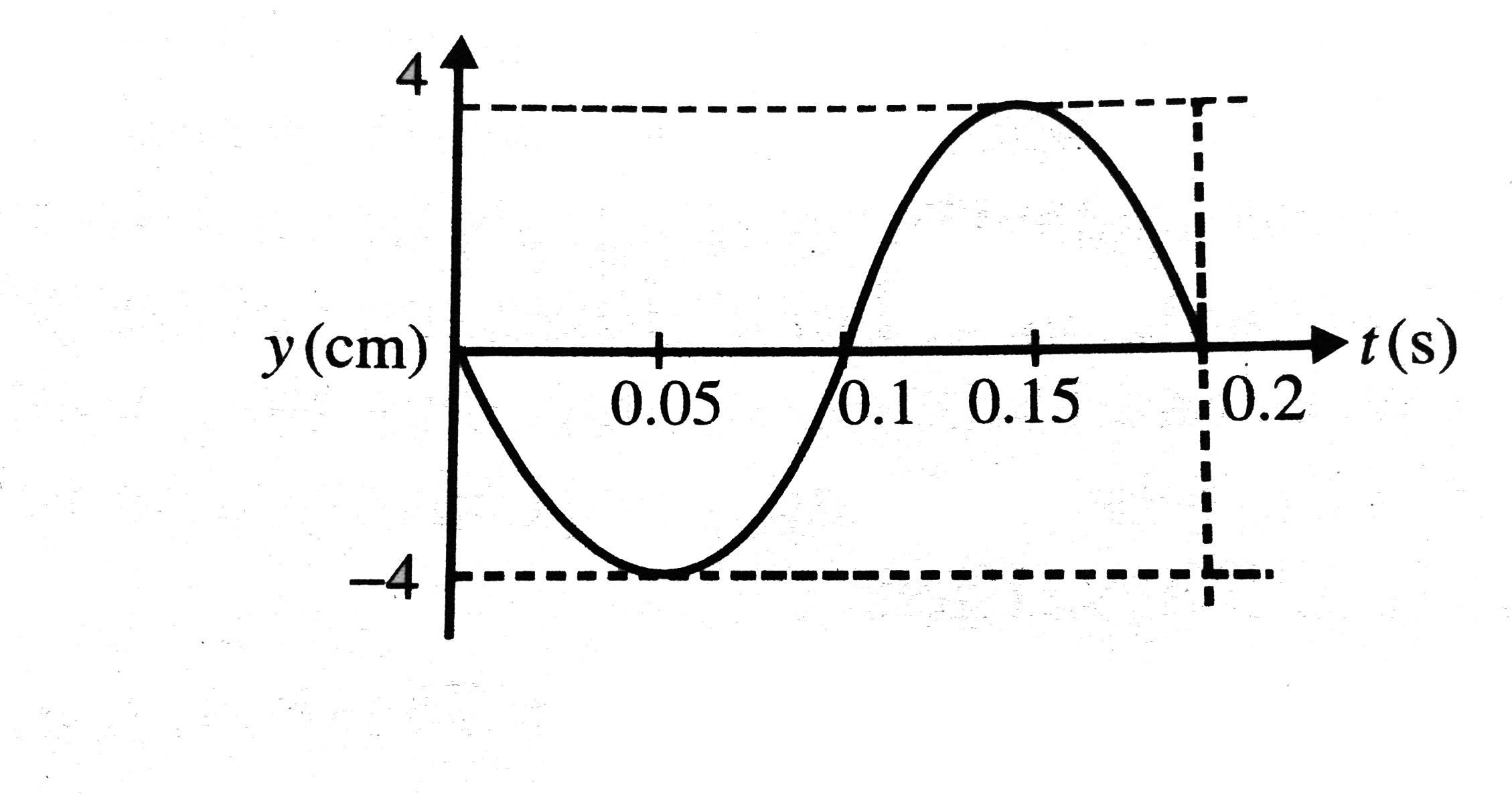 View Solution
View SolutionA string of linear mass density 5.0×10−3 kg//m is stretched under a tension of 65 N between two rigid supports 60 cm apart.
(a) If the string is vibrating in its second overtone so that the amplitude at one of its antinodes is 0.25 cm, what are the maximum transverse speed and acceleration of the string at antinodes?
(b) What are these quantities at a distance 5.0 cm from an node?View SolutionThe equation of standing wave in a stretched string is given by {y=2sin[π2(x)]cos(20πt)} where x and y are in meter and t is in second. Then minimum separation between two particle which are at the antinodes and having same phase will be
View SolutionA string with tension T and mass per unit length μ is clamped down at x=0 and at x=L. at t=0, the string is at rest and displaced in the y-direction
y(x,0)=2sin2πxL+3sinπxL
Q. What is the total energy at t=0?View SolutionA 2 m-long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s and the amplitude is 0.5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x= 50 cm has reached its maximum displacement.
View SolutionS1 : A standing wave pattern if formed in a string. The power transfer through a point (other than node and antinode) is zero always
S2: if the equation of transverse wave is y=sin2π[t0.04−x40], where distance is in cm. time in second, then the wavelength will be 40 cm.
S3: if the length of the vibrating string is kept constant, then frequency of the string will be directly proportional to √TView SolutionA string 120cm in length sustains a standing wave with the points of the string aat which the displacement amplitude is equal to 3.5mm being separated by 15.0cm. Find the maximum displacement amplitude . To which overtone do these oscillations correspond ?
View Solution

