The surface temperature of the sun is T0 and it is at average distance d from a planet. The radius of the sun is R. The temperature at which planet radiates the energy is
T0√R2d
T0√2Rd
T0√Rd
T0(Rd)1/4
The correct Answer is:(a)
To solve the problem, we need to find the temperature at which the planet radiates energy, given the surface temperature of the sun T0, the radius of the sun R, and the average distance from the sun to the planet d.
1. Understanding the Concept of Thermal Equilibrium:
- The planet is in thermal equilibrium with the sun, meaning the power radiated by the sun is equal to the power absorbed by the planet.
2. Power Radiated by the Sun:
- According to the Stefan-Boltzmann law, the power P radiated by a black body is given by:
P=σAT4
- For the sun, the area A is the surface area of a sphere, which is 4πR2. Therefore, the power radiated by the sun is:
Psun=σ(4πR2)T40
3. Power Received by the Planet:
- The planet is at a distance d from the sun, so the power received by the planet can be calculated using the same Stefan-Boltzmann law. The effective area from which the planet receives the solar radiation is 4πd2:
Pplanet=σ(4πd2)T4
4. Setting the Powers Equal:
- Since the planet is in thermal equilibrium, we set the power radiated by the sun equal to the power received by the planet:
σ(4πR2)T40=σ(4πd2)T4
5. Canceling Common Terms:
- We can cancel σ and 4π from both sides:
R2T40=d2T4
6. Rearranging the Equation:
- Rearranging gives us:
T4=R2d2T40
7. Taking the Fourth Root:
- To find T, we take the fourth root of both sides:
T=(R2d2)1/4T0=R1/2d1/2T0
Final Answer:
The temperature at which the planet radiates energy is:
T=R1/2d1/2T0
- The planet is in thermal equilibrium with the sun, meaning the power radiated by the sun is equal to the power absorbed by the planet.
- According to the Stefan-Boltzmann law, the power P radiated by a black body is given by:
P=σAT4
- For the sun, the area A is the surface area of a sphere, which is 4πR2. Therefore, the power radiated by the sun is:
Psun=σ(4πR2)T40
- The planet is at a distance d from the sun, so the power received by the planet can be calculated using the same Stefan-Boltzmann law. The effective area from which the planet receives the solar radiation is 4πd2:
Pplanet=σ(4πd2)T4
- Since the planet is in thermal equilibrium, we set the power radiated by the sun equal to the power received by the planet:
σ(4πR2)T40=σ(4πd2)T4
- We can cancel σ and 4π from both sides:
R2T40=d2T4
- Rearranging gives us:
T4=R2d2T40
- To find T, we take the fourth root of both sides:
T=(R2d2)1/4T0=R1/2d1/2T0
The temperature at which the planet radiates energy is:
T=R1/2d1/2T0
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Multiple Correct Answer
2 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Comprehension
4 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Fill in the blanks type
6 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
Similar Questions
Knowledge Check
If the temperature of the Sun were to increase from T to 2T and its radius from R to 2R. The rat io of power, radiated by it would become
A64 timesB16 timesC32 timesD4 times
In the previous problem, if θ is the angle sbtended by the Sun at the planet, then temperature at which planet radiates energy is proportional to
View SolutionThe solar constant is the amount of heat energy received per second per unit area of a perfectly black surface placed at a mean distance of the Earth form the Sun, in the absence of Earth's atmosphere, the surface being held perpendicular to the direction of Sun's rays. Its value is 1388W/m2. If the solar constant for the earth is 's'. The surface temperature of the sun is TK,D is the diameter of the sun, R is the mean distance of the Earth from the sun. The sun subtends a small angle 'theta' at the earth. Then correct options is/are:-
View SolutionThe solar constant for a planet is S. The surface temperature of the sun is TK. The sun subtends an angle θ at the planet:
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
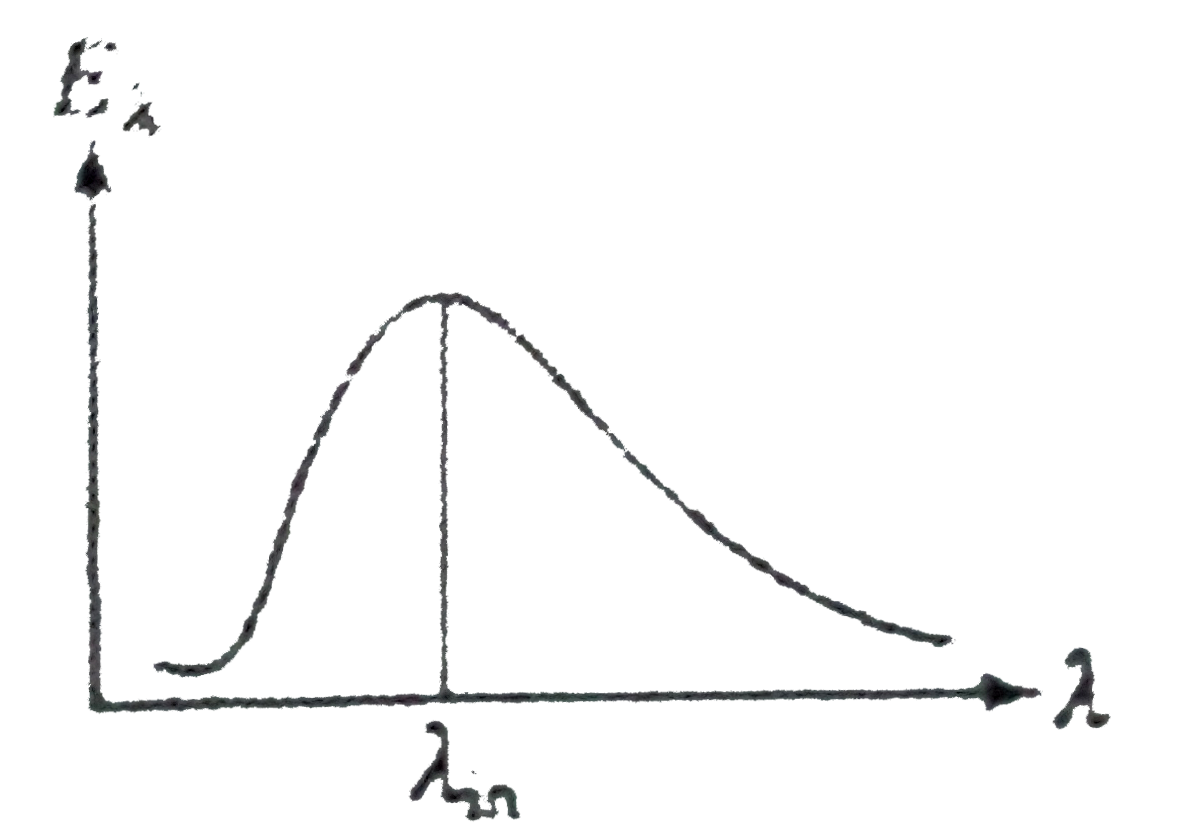
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
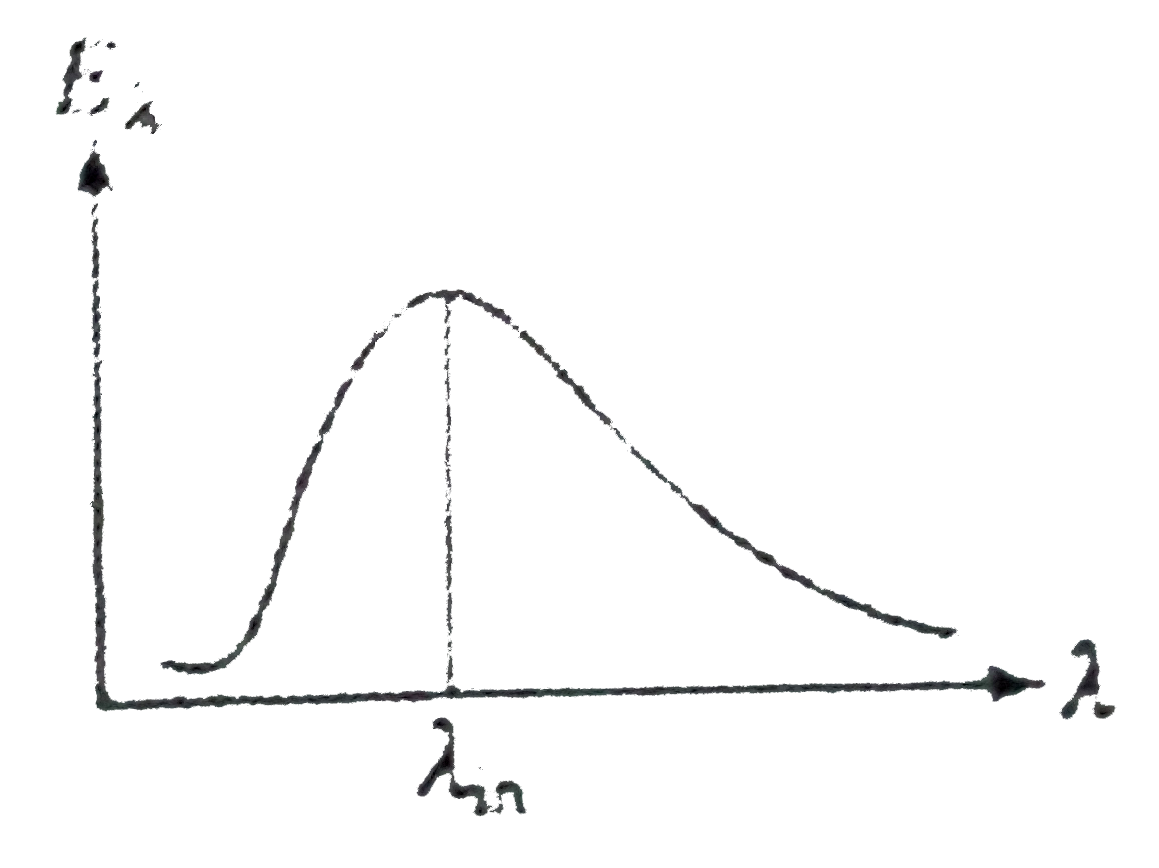
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?
View SolutionRadiation energy corresponding to the temperature T of the sun is E. If its temperature is doubled, then its radiation energy will be :
View SolutionThe sun having surface temperature Ts radiates like a black body. The rasius of sun is Rs and earth is at a distance R from the surface of sun. Earth absorbs radiations falling on its surface from sun only and is at constant temperature T. If radiations falling on earth's surface are alomost parallel and earth also radiates like a blackbody, then
View Solution
