The thermal conductivity of a material in CGS system is 0.4. In steady state, the rate of flow of heat 10 cal/sec-cm, then the thermal gradient will be
The correct Answer is:25∘C/cm
To find the thermal gradient (dT/dx) given the thermal conductivity and the rate of heat flow, we can use Fourier's law of heat conduction, which states:
Q=k⋅A⋅dTdx
Where:
- Q is the rate of heat flow (in cal/sec),
- k is the thermal conductivity (in cal/sec-cm-°C),
- A is the area through which heat is flowing (in cm²),
- dTdx is the thermal gradient (in °C/cm).
In this case, we are given:
- k=0.4cal/sec-cm-°C
- Q=10cal/sec-cm
Since the area A is not specified, we can assume it to be 1 cm² for simplicity. Thus, the equation simplifies to:
Q=k⋅dTdx
Now, we can rearrange this equation to solve for the thermal gradient dTdx:
dTdx=Qk
Substituting the known values into the equation:
dTdx=10cal/sec-cm0.4cal/sec-cm-°C
Calculating this gives:
dTdx=100.4=25°C/cm
Thus, the thermal gradient dTdx is:
Final Answer: 25 °C/cm
---
- Q is the rate of heat flow (in cal/sec),
- k is the thermal conductivity (in cal/sec-cm-°C),
- A is the area through which heat is flowing (in cm²),
- dTdx is the thermal gradient (in °C/cm).
- k=0.4cal/sec-cm-°C
- Q=10cal/sec-cm
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single Corrct Answer
7 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Multiple Correct Answer
2 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Comprehension type
4 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
Similar Questions
A cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder is k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylinder is :
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionA falt-bottom kettle placed on a stove is being used to boil water. The area of the bottom is 270cm2 the thickness is 0.3 cm and the thermal conductivity of the material is 0.5cal/scm∘C. If the amount of steam being produced in the kettle is at the rate of 10 g per minute calculate the difference of temperature between the inner and outer surfaces of the bottom. The latent heat of steam is 540cal/gm.
View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View SolutionThe density of a material in CGS system is 2g/cm3. In a system of units in which unit of length is 2 cm and unit of mass is 4 g what is the numerical value of the density of the material?
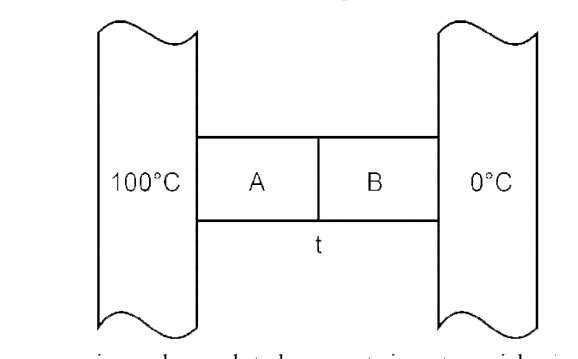
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are 300W/m∘Cand200W/m∘C, respectively. After steady state is reached the temperature t of the interface will be ......
View SolutionA cylindrical block of length 0.4 m and area of cross-section 0.04m2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is 10watt/m−K and the specific heat of the material of the disc is 600J/kg−K, how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.
View SolutionThe density of material in CGS system of mass is 4gcm3 in a system of unit in which unit of length is 10cm and unit of mass is 100g the value of density of material will be
View SolutionSteam at 373 K is passed through a tube of radius 10cm and length10cm and length 2m. The thickness of the tube is 5mm and thermal conductivity of the material is390Wm−1K−1, calculate the heat lost per second. The outside temperature is 0∘C.
View SolutionA point source of heat is placed at the centre of a spherical shell of mean radius 10 cm. the material of the shell has thermal conductivity 9.5×10−2kcal/m−s∘C. Calculate the power of point source of heat, when the temperature difference between the outer and inner surface of the shell is 50∘C in steady state. the thickness of shell is 2 cm.
View Solution
