A proton (mass m and charge +e) and an α-particle (mass 4 m and charge +2e) are projected with the same kinetic energy at right angles to the uniform magnetic field. Which one of the following statements will be true?
The α-particle will be bent in a circular path with a small radius that for the proton
The radius of the path of the α-particle will be greater than that of the proton
The α-particle and the proton will be bent in a circular path with the same radiuys
The α-particle and the proton will go through the field in a straight line
The correct Answer is:C
To solve the problem, we need to analyze the motion of a proton and an alpha particle in a magnetic field when they are projected with the same kinetic energy at right angles to the field.
1. Understanding the Motion in a Magnetic Field:
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path depends on the mass of the particle, its charge, and its velocity.
2. Formula for Radius of Circular Motion:
The radius r of the circular path of a charged particle in a magnetic field is given by:
r=mvqB
where:
- m = mass of the particle
- v = velocity of the particle
- q = charge of the particle
- B = magnetic field strength
3. Kinetic Energy Relation:
The kinetic energy K of a particle is given by:
K=12mv2
From this, we can express the velocity v in terms of kinetic energy:
v=√2Km
4. Substituting Velocity into the Radius Formula:
Substituting the expression for v into the radius formula gives:
r=m√2KmqB=√2KmqB
5. Calculating Radius for Proton:
For the proton (mass m, charge +e):
rp=√2KmeB
6. Calculating Radius for Alpha Particle:
For the alpha particle (mass 4m, charge +2e):
rα=√2K(4m)2eB=2√2Km2eB=√2KmeB
7. Comparing the Radii:
From the above calculations, we see:
rp=√2KmeBandrα=√2KmeB
This shows that the radius of the circular path for both the proton and the alpha particle is the same.
8. Conclusion:
Since both particles have the same radius of curvature in the magnetic field, we conclude that the correct statement is:
- The alpha particle and the proton will be bent in a circular path with the same radius.
Final Answer:
The correct option is that the alpha particle and the proton will be bent in a circular path with the same radius.
---
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path depends on the mass of the particle, its charge, and its velocity.
The radius r of the circular path of a charged particle in a magnetic field is given by:
r=mvqB
where:
- m = mass of the particle
- v = velocity of the particle
- q = charge of the particle
- B = magnetic field strength
The kinetic energy K of a particle is given by:
K=12mv2
From this, we can express the velocity v in terms of kinetic energy:
v=√2Km
Substituting the expression for v into the radius formula gives:
r=m√2KmqB=√2KmqB
For the proton (mass m, charge +e):
rp=√2KmeB
For the alpha particle (mass 4m, charge +2e):
rα=√2K(4m)2eB=2√2Km2eB=√2KmeB
From the above calculations, we see:
rp=√2KmeBandrα=√2KmeB
This shows that the radius of the circular path for both the proton and the alpha particle is the same.
Since both particles have the same radius of curvature in the magnetic field, we conclude that the correct statement is:
- The alpha particle and the proton will be bent in a circular path with the same radius.
The correct option is that the alpha particle and the proton will be bent in a circular path with the same radius.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Comprehension type
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Subjective
11 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Assertion-reasion
1 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A proton and an alpha particle is projected with equal kinetic energy in transverse uniform magnetic field B. The ratio of radii of proton to that of alpha particle is
View SolutionThe change in the kinetic energy of a charged particle moving in a uniform magnetic field will be zero when its velocity is
View Solution
Knowledge Check
An electron and a proton enter a magnetic field at right angles to the field with the same kinetic energy
Athe electron trajectory will be less curved than the proton trajectoryBthe proton trajectory will be less curved than the electron trajectoryCboth trajectories will be equally curvedDboth particles move in straight lines
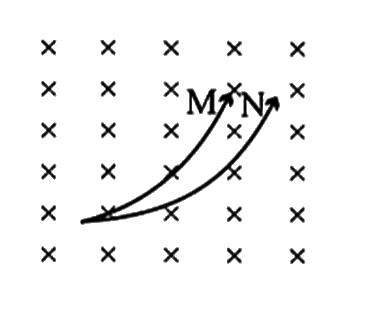
Two charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA particle of mass m, charge q and kinetic energy T enters in a transverse uniform magnetic field of induction B. After the 3 s, the kinetic energy of the particle will be
View SolutionA proton and an alpha particle projected with same velocity in uniform transverse magnetic field then
View SolutionA charge q of mass m is moving with a velocity of V, at right angles to a uniform magnetic field B. Deduce the expression for the radius of the circular path it describes.
View SolutionAn electron having mass 'm' and kinetic energy E enter in uniform magnetic field B perpendicularly, then its frequency will be : -
View Solution
