A double slit is illuminated by the light of wavelength 12000A .The slits are 0.1 cm apart and the screen is placed one metre away.calculate the angular posiyion of 10 maximum in radians ?
The correct Answer is:B
To solve the problem of finding the angular position of the 10th maximum in a double-slit experiment, we will follow these steps:
1. Identify the Given Data:
- Wavelength (λ) = 12000 Å (angstroms)
- Distance between slits (d) = 0.1 cm
- Distance to the screen (D) = 1 m
- Order of maximum (n) = 10
2. Convert Units:
- Convert the wavelength from angstroms to meters:
λ=12000Å=12000×10−10m=12×10−7m
- Convert the distance between slits from centimeters to meters:
d=0.1cm=0.1×10−2m=1×10−3m
3. Use the Formula for Angular Position:
- The formula for the angular position of the n-th maximum in a double-slit experiment is:
dsinθ=nλ
- For small angles, sinθ≈θ (in radians), so we can rewrite the equation as:
θ=nλd
4. Substitute the Values:
- Substitute n=10, λ=12×10−7m, and d=1×10−3m into the equation:
θ=10×(12×10−7)1×10−3
5. Calculate θ:
- Perform the calculation:
θ=120×10−710−3=120×10−4=12×10−3radians
6. Final Result:
- The angular position of the 10th maximum is:
θ=0.012radians
- Wavelength (λ) = 12000 Å (angstroms)
- Distance between slits (d) = 0.1 cm
- Distance to the screen (D) = 1 m
- Order of maximum (n) = 10
- Convert the wavelength from angstroms to meters:
λ=12000Å=12000×10−10m=12×10−7m
- Convert the distance between slits from centimeters to meters:
d=0.1cm=0.1×10−2m=1×10−3m
- The formula for the angular position of the n-th maximum in a double-slit experiment is:
dsinθ=nλ
- For small angles, sinθ≈θ (in radians), so we can rewrite the equation as:
θ=nλd
- Substitute n=10, λ=12×10−7m, and d=1×10−3m into the equation:
θ=10×(12×10−7)1×10−3
- Perform the calculation:
θ=120×10−710−3=120×10−4=12×10−3radians
- The angular position of the 10th maximum is:
θ=0.012radians
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Subjective11videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Single Correct Answer Type42videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
A double slit is illuminated by light of wave length 6000 Å. The slit are 0.1 cm apart and the screen is placed one metre away. Calculate.
(i). The angular position of the 10th maximum in radian and
(ii). Separation of the two adjacent minimal.View SolutionA double slit is illuminated by the light of wavelength 12000A .The slits are 0.1 cm apart and the screen is placed one metre away.calculate the sepration between the two adjacent minima?
View Solution
Knowledge Check
- Question 1 - Select One
A single slit is illuminated by light of wavelength 6000 Ã…. The slit width is 0.1 cm and the screen is placed 1 m away. The angular position of 10th minimum in radian is
A2×10−4B6×10−3C3×10−3D1×10−4
A double slit is illuminated by light of wavelength 6000 Å. The slits are 0.1 cm apart and the screen is placed one metre away. calculate :
sepration between the two adjacent minimaView SolutionA double slit is illuminated by light of wavelength 12000 A .the slits are 0.1 cm apart and the screen is placed one metre away .find the sepration between the two adjacent minima?
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
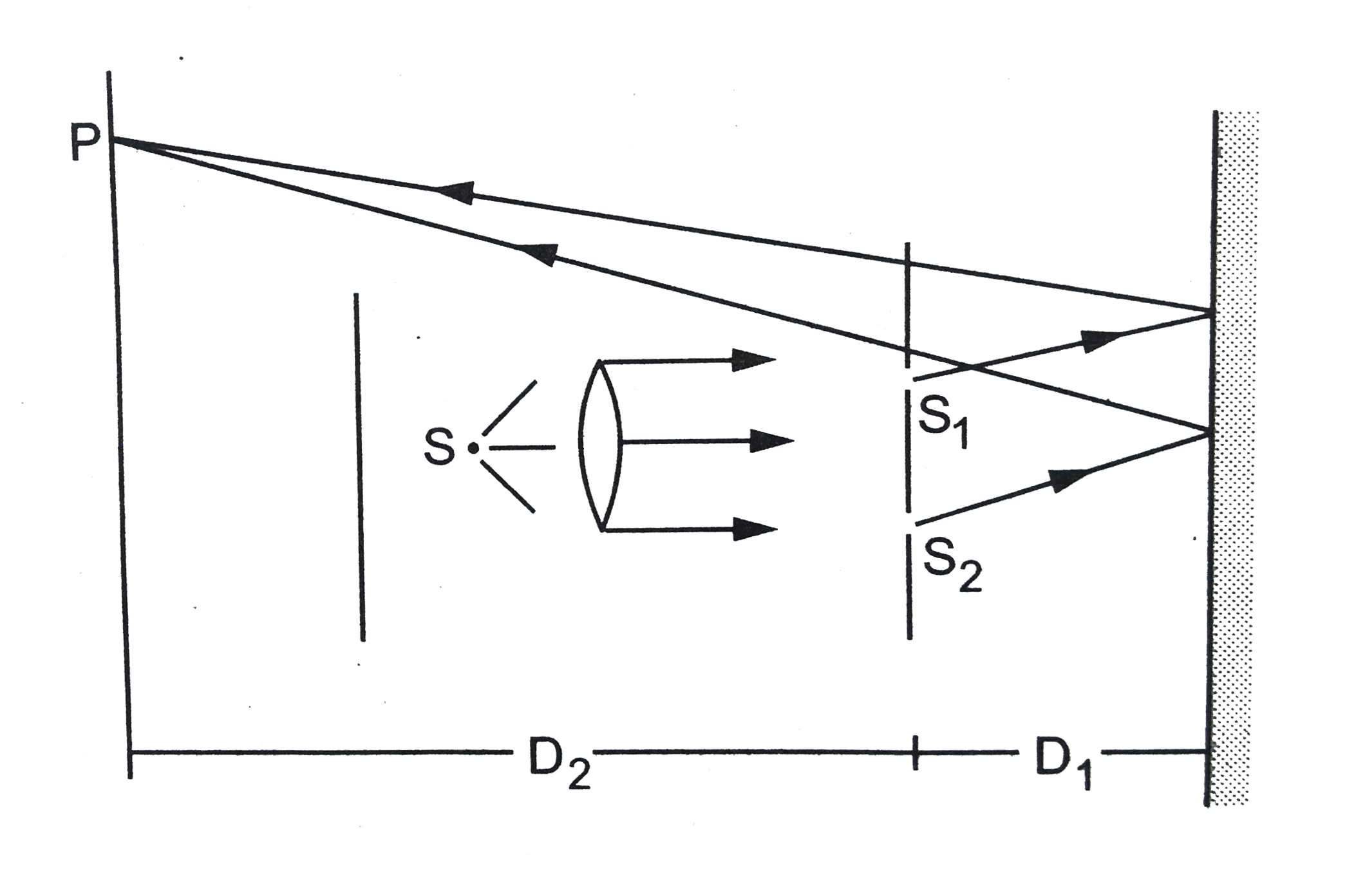 View Solution
View SolutionIn Young.s double slit experiment, blue-green light of wavelength 500nm is used. The slits are 1.20mm apart, and the viewing screen is 5.40m away from the slits. What is the fringe width.
View SolutionIn YDSE a=2mm, D = 2m, λ=500 nm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionThe Young's double slit experiment is carried out with light of wavelength 5000Å. The distance between the slits is 0.2mm and the screen is at 200cm from the slits. The central maximum is at y=0. The third maximum will be at y equal to
View SolutionTwo slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
View Solution

