A metallic rod of mass per unit length is lying horizontally on a straght inclined plane which makes an angle of with the horizontal. The rod is not allowed to slide down by flowing a current throguh it when a magnetic field of induction is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is
14.76 A
5.98 A
7.14 A
11.32 A
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the metallic rod and apply the necessary physics principles.
Step 1: Identify the forces acting on the rod
The rod is subjected to two main forces:
1. The gravitational force acting downwards, Fg=mg.
2. The magnetic force acting perpendicular to the current and magnetic field, Fm=IBL.
Step 2: Calculate the gravitational force component along the incline
The gravitational force can be resolved into two components:
- Perpendicular to the incline: Fg⊥=mgcos(θ)
- Parallel to the incline (down the slope): Fg∥=mgsin(θ)
Step 3: Set up the equilibrium condition
For the rod to remain stationary on the incline, the magnetic force must balance the gravitational force component acting down the slope:
Fm=Fg∥
Thus,
IBL=mgsin(θ)
Step 4: Substitute known values
Given:
- Mass per unit length, mL=0.5kg/m
- Gravitational acceleration, g=9.8m/s2
- Angle of incline, θ=30∘
- Magnetic field, B=0.25T
From the mass per unit length, we can express m as:
m=mL⋅L=0.5L
Now substituting into the equilibrium equation:
IBL=(0.5L)(9.8)sin(30∘)
Step 5: Simplify the equation
Since sin(30∘)=0.5:
IBL=(0.5L)(9.8)(0.5)
IBL=0.25L⋅9.8
IBL=2.45L
Step 6: Cancel L from both sides
Assuming L is not zero, we can cancel L:
IB=2.45
Step 7: Solve for current I
Now we can solve for I:
I=2.45B
Substituting B=0.25T:
I=2.450.25
I=9.8A
Step 8: Final calculation
To find the current, we can also use the mass per unit length directly:
I=m/L⋅g⋅sin(30∘)B
Substituting the values:
I=0.5⋅9.8⋅0.50.25
I=2.450.25
I=9.8A
Final Answer
The current flowing in the rod to keep it stationary is:
I=9.8A
The rod is subjected to two main forces:
1. The gravitational force acting downwards, Fg=mg.
2. The magnetic force acting perpendicular to the current and magnetic field, Fm=IBL.
The gravitational force can be resolved into two components:
- Perpendicular to the incline: Fg⊥=mgcos(θ)
- Parallel to the incline (down the slope): Fg∥=mgsin(θ)
For the rod to remain stationary on the incline, the magnetic force must balance the gravitational force component acting down the slope:
Fm=Fg∥
Thus,
IBL=mgsin(θ)
Given:
- Mass per unit length, mL=0.5kg/m
- Gravitational acceleration, g=9.8m/s2
- Angle of incline, θ=30∘
- Magnetic field, B=0.25T
m=mL⋅L=0.5L
IBL=(0.5L)(9.8)sin(30∘)
Since sin(30∘)=0.5:
IBL=(0.5L)(9.8)(0.5)
IBL=0.25L⋅9.8
IBL=2.45L
Assuming L is not zero, we can cancel L:
IB=2.45
Now we can solve for I:
I=2.45B
Substituting B=0.25T:
I=2.450.25
I=9.8A
To find the current, we can also use the mass per unit length directly:
I=m/L⋅g⋅sin(30∘)B
Substituting the values:
I=0.5⋅9.8⋅0.50.25
I=2.450.25
I=9.8A
The current flowing in the rod to keep it stationary is:
I=9.8A
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - AIIMS22videos
SOLVED PAPERS 2018
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons10videos
SOLVED PAPERS 2018
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)32videos
SOLVED PAPER 2017
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions13videos
WAVE OPTICS
Similar Questions
A block slides down a frictionless, inclined plane that makes a 30∘ angle with the horizontal. Find the acceleration of this block.
View SolutionA brick of mass 2kg begins to slide down on a plane inclined at an angle of 45∘ with the horizontal. The force of friction will be
View SolutionAn inclined plane makes an angle 30° with the horizontal. A solid sphere rolling down this inclined plane from rest without slipping has a linear acceleration equal to
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
View SolutionA block is lying on an inclined plane which makes an angle of 60∘ with the horizontal. If coefficient of friction between the block and the plane is 0.25 and g = 10 ms−2, the acceleration of block when it is moves along the plane will be
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
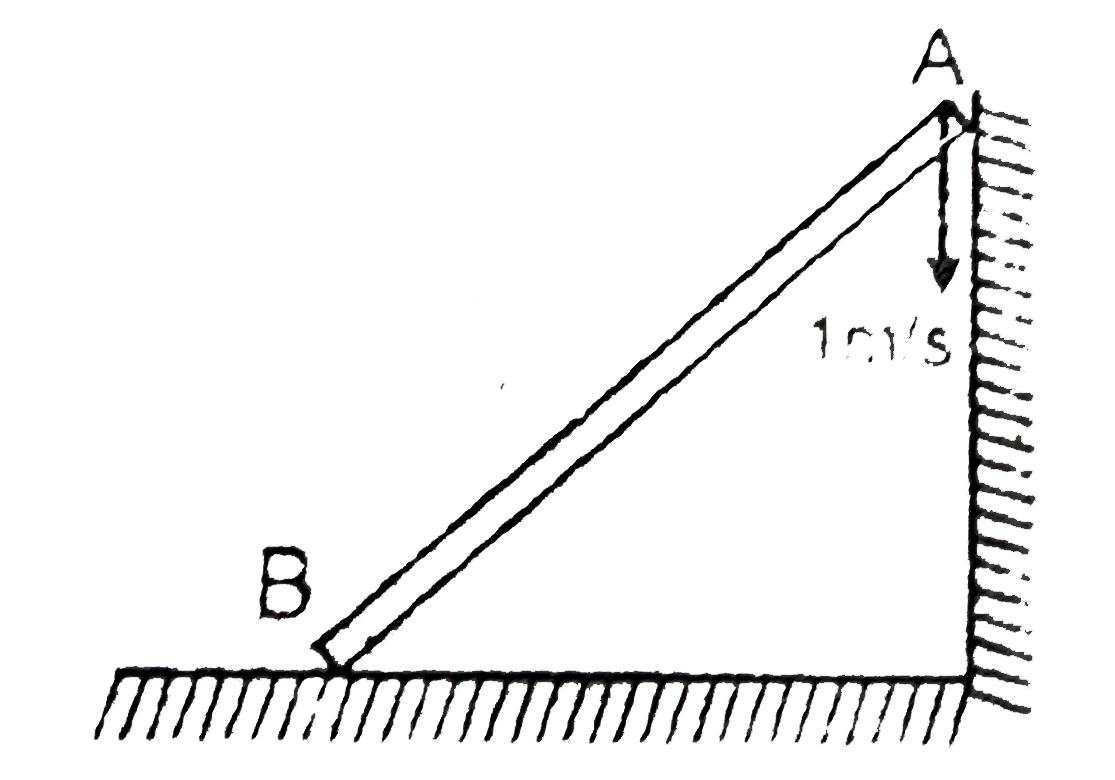 View Solution
View SolutionA horizontal rod of mass 10g and length 10cm is placed on a smooth plane inclined at an angle of 60∘ with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is 1⋅73ampere, the value of B for which the rod remains stationary on the inclined plane is
View SolutionA horizontal rod of mass 10g and length 10cm is placed on a smooth plane inclined at an angle of 60∘ with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is 1⋅73ampere, the value of B for which the rod remains stationary on the inclined plane is
View Solution

