A thin circular wire carrying a current I has a magnetic moment M. The shape of the wire is changed to a square and it carries the same current. It will have a magnetic moment
M
4π2M
4πM
π4M
The correct Answer is:D
To solve the problem, we need to determine the magnetic moment of a square wire carrying the same current as a circular wire. Let's go through the steps systematically.
Step 1: Understand the Magnetic Moment of a Circular Wire
The magnetic moment M of a circular wire carrying current I is given by the formula:
M=I⋅A
where A is the area enclosed by the loop. For a circular wire of radius r, the area A is:
A=πr2
Thus, the magnetic moment for the circular wire can be expressed as:
M=I⋅πr2
Step 2: Relate the Circumference of the Circle to the Side of the Square
When the shape of the wire is changed from a circle to a square, the length of the wire remains the same. The circumference of the circle is:
C=2πr
For a square with side length a, the perimeter is:
P=4a
Setting these equal gives:
2πr=4a⟹a=πr2
Step 3: Calculate the Area of the Square
The area A′ of the square is given by:
A′=a2=(πr2)2=π2r24
Step 4: Calculate the Magnetic Moment of the Square Wire
The magnetic moment M′ of the square wire carrying the same current I is:
M′=I⋅A′=I⋅π2r24
Step 5: Relate the Magnetic Moments of the Circle and Square
Now, we can find the ratio of the magnetic moment of the square wire to that of the circular wire:
M′M=I⋅π2r24I⋅πr2=π2r24πr2=π4
Thus, we can express M′ in terms of M:
M′=π4M
Final Answer
The magnetic moment of the square wire is:
M′=π4M
The magnetic moment M of a circular wire carrying current I is given by the formula:
M=I⋅A
where A is the area enclosed by the loop. For a circular wire of radius r, the area A is:
A=πr2
Thus, the magnetic moment for the circular wire can be expressed as:
M=I⋅πr2
When the shape of the wire is changed from a circle to a square, the length of the wire remains the same. The circumference of the circle is:
C=2πr
For a square with side length a, the perimeter is:
P=4a
Setting these equal gives:
2πr=4a⟹a=πr2
The area A′ of the square is given by:
A′=a2=(πr2)2=π2r24
The magnetic moment M′ of the square wire carrying the same current I is:
M′=I⋅A′=I⋅π2r24
Now, we can find the ratio of the magnetic moment of the square wire to that of the circular wire:
M′M=I⋅π2r24I⋅πr2=π2r24πr2=π4
Thus, we can express M′ in terms of M:
M′=π4M
The magnetic moment of the square wire is:
M′=π4M
Similar Questions
Two wires of the same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View SolutionTwo wires of same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View SolutionA square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. If this square loop is changed to a circular loop and it carries the same current, the magnitude of the magnetic dipole moment of circular loop will be:
View SolutionA square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this square loop is changed to a circular loop and it carries the current, the magnitude of the magnetic dipole moment of circular loop will be :
View SolutionA square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this square loop is changed to a circular loop and it carries the current, the magnitude of the magnetic dipole moment of circular loop will be :
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is
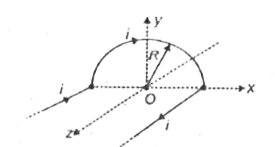
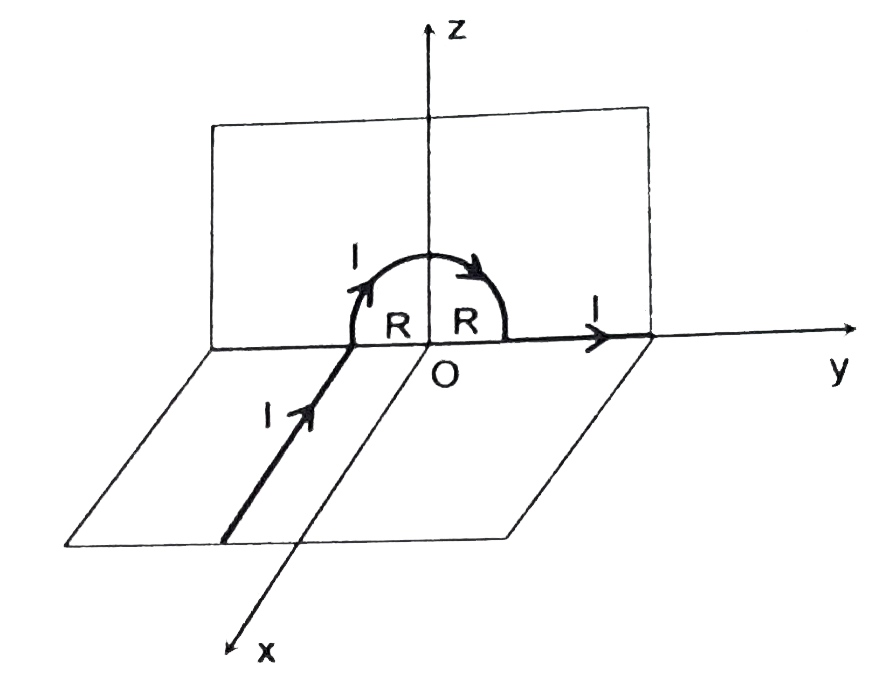
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
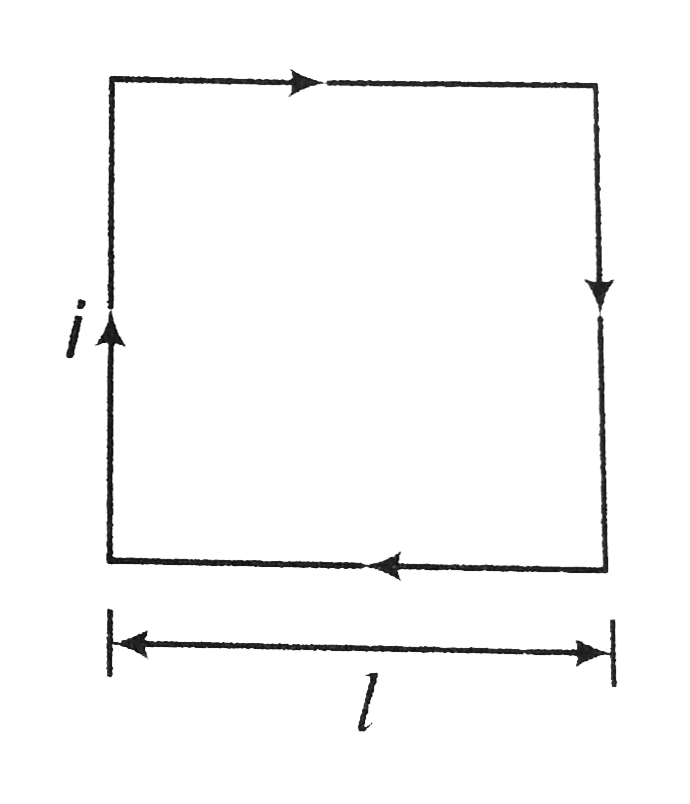
View Solutiona. A conductor in the shape of a square of edge length l=0.4m carries a current i=10.0A. Calculate the magnitude and direction of magnetic field at the centre of the square.
b. If this conductor is formed into a single circular turn and carries the same current. what is the value of the magnetic field at the centre.
View SolutionA metallic wire is folded to form a square loop a side 'a'. It carries a current 'I' and is kept perpendicular to a uniform magnetic field. If the shape of the loop is changed from square to a circle without changing the length of thw wire and current, the amount of work done in doing so is
View SolutionCalculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
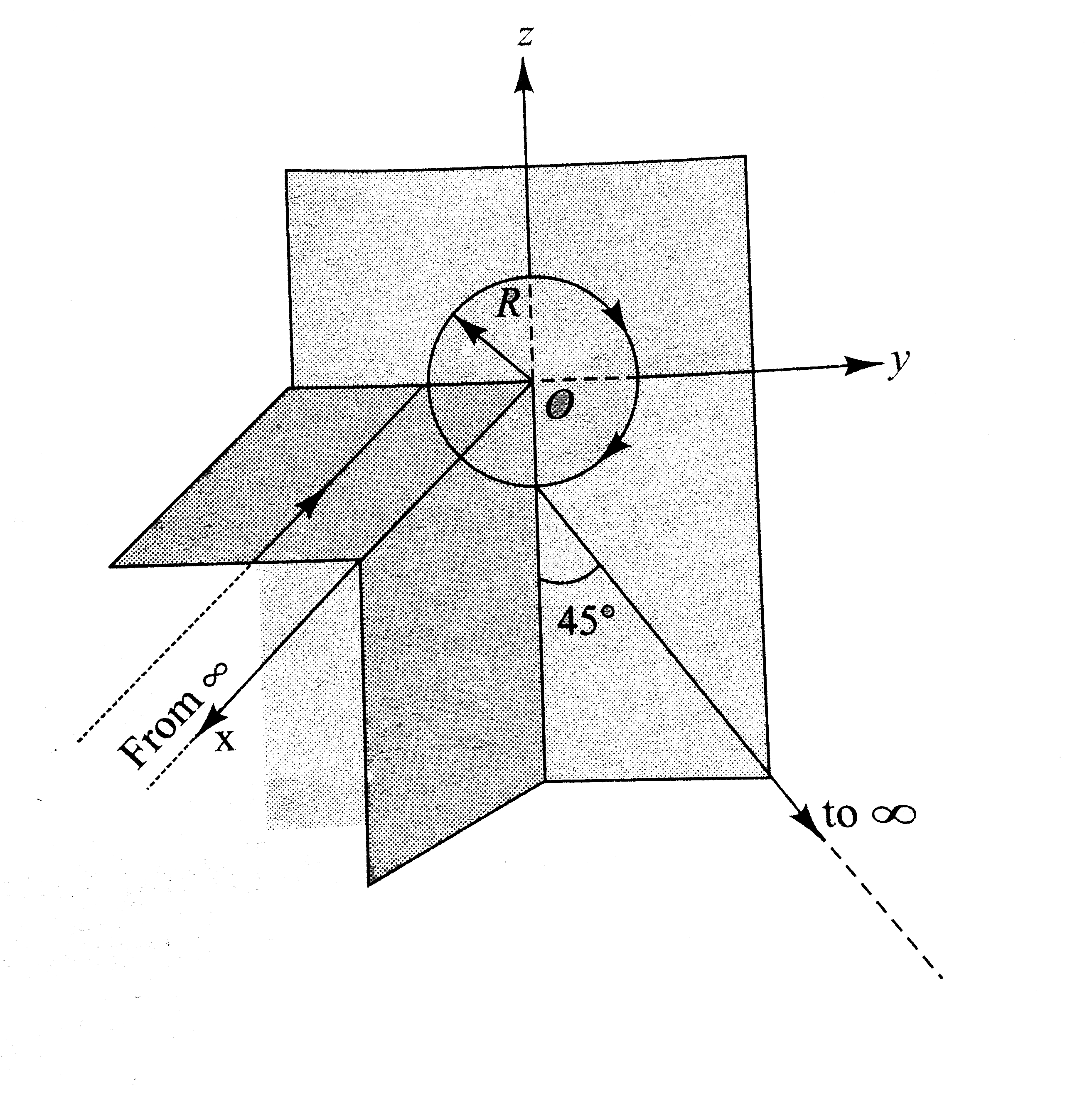
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
View Solution