A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this square loop is changed to a circular loop and it carries the current, the magnitude of the magnetic dipole moment of circular loop will be :
4mπ
2mπ
3mπ
mπ
The correct Answer is:A
To solve the problem step by step, we will analyze the magnetic dipole moment of both the square loop and the circular loop.
Step 1: Understanding the Magnetic Dipole Moment of the Square Loop
The magnetic dipole moment m of a square loop carrying a current I can be expressed using the formula:
m=n⋅I⋅A
where:
- n is the number of turns (for a single loop, n=1),
- I is the current,
- A is the area of the loop.
For a square loop with side length A:
A=A2
Thus, the magnetic dipole moment becomes:
m=I⋅A2
Let's denote this as Equation (1).
Step 2: Finding the Magnetic Dipole Moment of the Circular Loop
When the square loop is transformed into a circular loop with the same perimeter, we need to find the radius r of the circular loop. The perimeter of the square loop is:
Perimeter of square=4A
The circumference of the circular loop is:
Circumference of circle=2πr
Setting these equal gives:
4A=2πr
From this, we can solve for r:
r=4A2π=2Aπ
Step 3: Area of the Circular Loop
The area A′ of the circular loop is given by:
A′=πr2
Substituting r=2Aπ:
A′=π(2Aπ)2=π⋅4A2π2=4A2π
Step 4: Magnetic Dipole Moment of the Circular Loop
Now, substituting the area A′ into the formula for the magnetic dipole moment of the circular loop m′:
m′=I⋅A′=I⋅4A2π
Step 5: Relating m′ to m
From Equation (1), we know that m=I⋅A2. Thus, we can express m′ in terms of m:
m′=4πm
Conclusion
The magnitude of the magnetic dipole moment of the circular loop is:
m′=4mπ
Final Answer
The magnitude of the magnetic dipole moment of the circular loop will be 4mπ.
---
The magnetic dipole moment m of a square loop carrying a current I can be expressed using the formula:
m=n⋅I⋅A
where:
- n is the number of turns (for a single loop, n=1),
- I is the current,
- A is the area of the loop.
A=A2
Thus, the magnetic dipole moment becomes:
m=I⋅A2
Let's denote this as Equation (1).
When the square loop is transformed into a circular loop with the same perimeter, we need to find the radius r of the circular loop. The perimeter of the square loop is:
Perimeter of square=4A
The circumference of the circular loop is:
Circumference of circle=2πr
Setting these equal gives:
4A=2πr
From this, we can solve for r:
r=4A2π=2Aπ
The area A′ of the circular loop is given by:
A′=πr2
Substituting r=2Aπ:
A′=π(2Aπ)2=π⋅4A2π2=4A2π
Now, substituting the area A′ into the formula for the magnetic dipole moment of the circular loop m′:
m′=I⋅A′=I⋅4A2π
From Equation (1), we know that m=I⋅A2. Thus, we can express m′ in terms of m:
m′=4πm
The magnitude of the magnetic dipole moment of the circular loop is:
m′=4mπ
The magnitude of the magnetic dipole moment of the circular loop will be 4mπ.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 250videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)10videos
MOCK TEST 1
Similar Questions
A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. If this square loop is changed to a circular loop and it carries the same current, the magnitude of the magnetic dipole moment of circular loop will be:
View SolutionMagnetic dipole moment of rectangular loop is
View SolutionThe magnetic dipole moment of current loop is independent of
View SolutionIn the given option,the magnetic dipole moment of current loop is independent of
View SolutionCompute the magnetic dipole moment of the loop shown in Fig. 1.69
 View Solution
View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
View SolutionA thin circular wire carrying a current I has a magnetic moment M. The shape of the wire is changed to a square and it carries the same current. It will have a magnetic moment
View SolutionA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
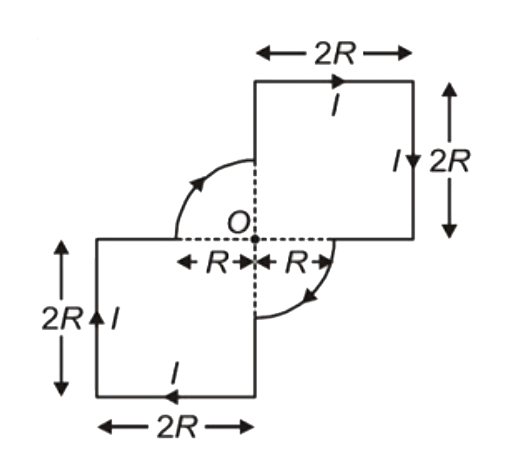 View Solution
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View Solution

