A winding wire which is used to frame a solenoid can bear a maximum 10 A. current If length of solenoid is 80 cm and its corss sectional raedius is 3 cm , then required length of winding wire is (B =0.2T)
1.2×102m
4.8×102m
2.4×103m
6×103m
The correct Answer is:C
To solve the problem step by step, we need to find the required length of the winding wire for the solenoid given the parameters.
Step 1: Understand the formula for the magnetic field in a solenoid
The magnetic field B inside a solenoid is given by the formula:
B=μ0NIL
where:
- B = magnetic field (0.2 T)
- μ0 = permeability of free space (4π×10−7T m/A)
- N = number of turns of the solenoid
- I = current (10 A)
- L = length of the solenoid (0.8 m)
Step 2: Rearrange the formula to find N
We can rearrange the formula to solve for N:
N=BLμ0I
Step 3: Substitute the known values into the equation
Substituting the known values into the equation:
N=0.2×0.84π×10−7×10
Step 4: Calculate N
Calculating the numerator:
0.2×0.8=0.16
Calculating the denominator:
4π×10−7×10=4π×10−6
Now substituting these values:
N=0.164π×10−6=0.161.25664×10−6≈127,323.95
So, rounding off, we get:
N≈4×104
Step 5: Calculate the total length of the wire
The total length of the wire Lw used in the solenoid can be calculated using the formula:
Lw=2πrN
where r is the radius of the solenoid (0.03 m).
Step 6: Substitute values to find Lw
Substituting the values:
Lw=2π×0.03×4×104
Step 7: Calculate Lw
Calculating:
Lw=2π×0.03×4×104≈2.4×103m
Final Answer
The required length of the winding wire is:
Lw≈2.4×103m
---
The magnetic field B inside a solenoid is given by the formula:
B=μ0NIL
where:
- B = magnetic field (0.2 T)
- μ0 = permeability of free space (4π×10−7T m/A)
- N = number of turns of the solenoid
- I = current (10 A)
- L = length of the solenoid (0.8 m)
We can rearrange the formula to solve for N:
N=BLμ0I
Substituting the known values into the equation:
N=0.2×0.84π×10−7×10
Calculating the numerator:
0.2×0.8=0.16
Calculating the denominator:
4π×10−7×10=4π×10−6
Now substituting these values:
N=0.164π×10−6=0.161.25664×10−6≈127,323.95
So, rounding off, we get:
N≈4×104
The total length of the wire Lw used in the solenoid can be calculated using the formula:
Lw=2πrN
where r is the radius of the solenoid (0.03 m).
Substituting the values:
Lw=2π×0.03×4×104
Calculating:
Lw=2π×0.03×4×104≈2.4×103m
The required length of the winding wire is:
Lw≈2.4×103m
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Answer Type
35 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
a. Calculate the inductance of an air core solenoid containing 300 turns if the length of the solenoid is 25.0cm and its cross -sectional area is 4.00cm2.
b. Calculate the self -induced emf in the solenoid if the current through it is decreasing at the rate of 50.0A/s.
View Solutiona. Calculate the inductance of an air core solenoid containing 300 turns if the length of the solenoid is 25.0cm and its cross -sectional area is 4.00cm2.
b. Calculate the self -induced emf in the solenoid if the current through it is decreasingg at the rate of 50.0A/s.
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mH
The length of thin wire required to manufacture a solenoid of inductance L and length l. (if the cross-sectional diameter is considered less than its length) is
View SolutionThe length of a thin wire required to manufacture a solenoid of lengthl=100cm and inductance L=1mH, if the solenoid's cross-sectional diameter is considerably less than its length is
View SolutionThe length of a wire required to manufacture a solenoid of length l and self-induction L is (cross-sectional area is negligible)
View SolutionA wire of cross-sectional area A breaks due to its own weight when length of the wire is l. If area of cross-section of the wire is made 3A then maximum length of the wire can be hung without breaking is
View SolutionA wire of length 3 cm has current 1 amp. Find magnetic field at a perpendicular distance a cm from centre of wire

View SolutionA current of 50A is placed through a straight wire of length 6cm then the magnetic induction at a point 5cm from the either end of the wire is (1gauss=10−4T)
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
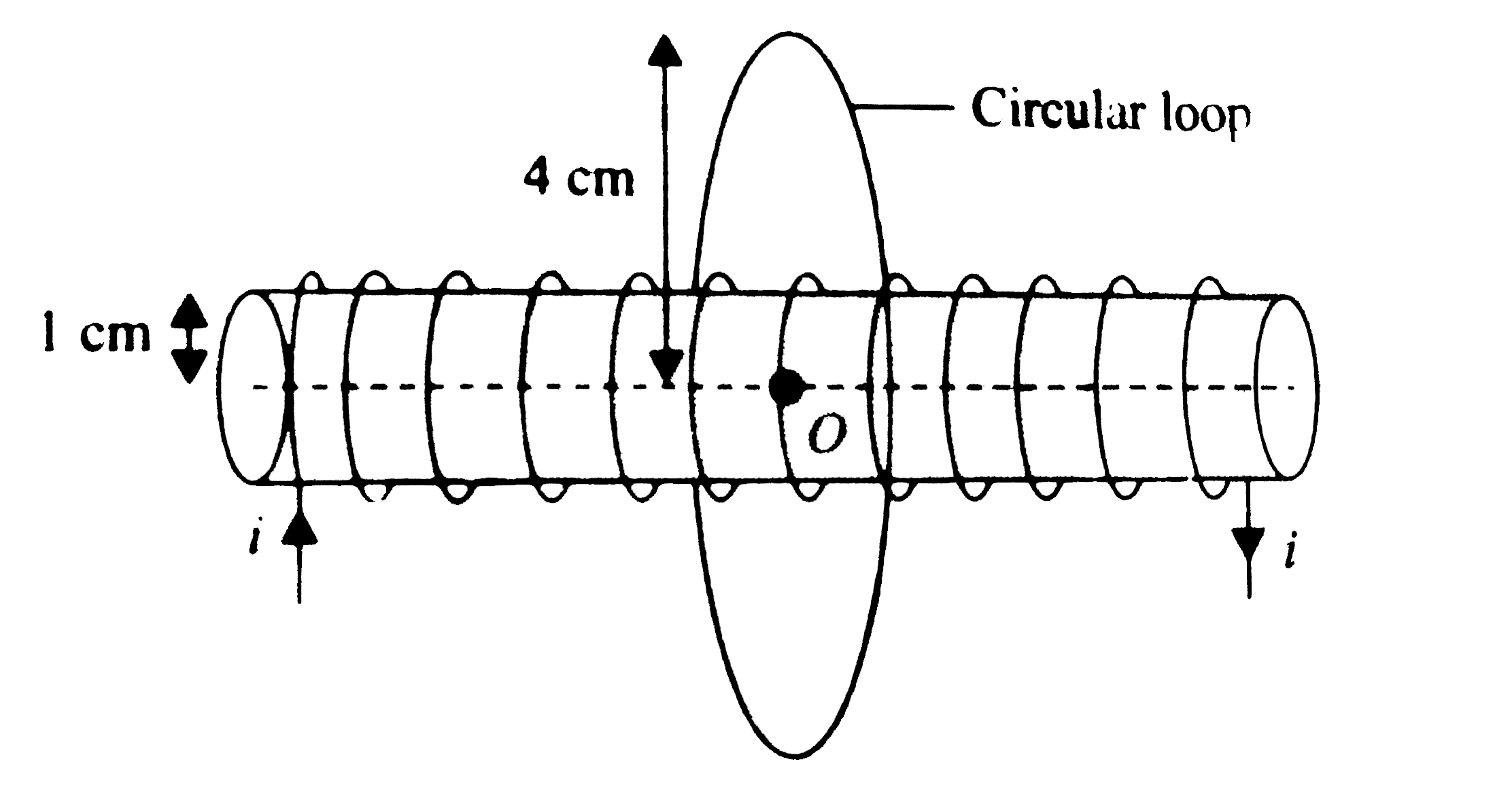
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View Solution
