A self-induced wmf in a solenoid of inductance L changes in time asɛ=ɛ0e−kz. Assuming the charge is finite.find the total charge that passes a point in the wire of the solenoid.
ɛ0Lk2
2ɛ0Lk2
ɛ02Lk2
3ɛ0Lk2
The correct Answer is:A
To solve the problem of finding the total charge that passes a point in the wire of a solenoid with a self-induced EMF given by ε=ε0e−kz, we can follow these steps:
Step 1: Relate EMF to Inductance and Current
The self-induced EMF in a solenoid can be expressed as:
ε=−Ldidt
Given that ε=ε0e−kz, we can equate the two expressions:
ε0e−kz=−Ldidt
Step 2: Rearranging the Equation
Rearranging the equation to isolate di:
didt=−ε0e−kzL
Step 3: Integrate to Find Current
We can now integrate both sides with respect to time t:
∫di=−ε0L∫e−ktdt
This gives:
i=−ε0L⋅(−1ke−kt)+C
where C is the constant of integration. Thus, we have:
i=ε0Lke−kt+C
Step 4: Relate Current to Charge
We know that current i is related to charge q by:
i=dqdt
Substituting for i:
dqdt=ε0Lke−kt+C
Step 5: Integrate to Find Total Charge
Now we can integrate to find the total charge q:
∫dq=∫(ε0Lke−kt+C)dt
This results in:
q=−ε0Lk2e−kt+Ct+Q0
where Q0 is another constant of integration.
Step 6: Evaluate Total Charge
Assuming the charge is finite and considering the limits of integration (from t=0 to t=∞), we can evaluate the charge:
q=(−ε0Lk2e−kt)∞0+C(t)∞0
As t→∞, e−kt→0, and at t=0, e−k⋅0=1:
q=−ε0Lk2(0−1)+C(∞−0)
The term with C becomes infinite unless C=0. Thus, we find:
q=ε0Lk2
Final Result
The total charge that passes a point in the wire of the solenoid is:
q=ε0Lk2
The self-induced EMF in a solenoid can be expressed as:
ε=−Ldidt
Given that ε=ε0e−kz, we can equate the two expressions:
ε0e−kz=−Ldidt
Rearranging the equation to isolate di:
didt=−ε0e−kzL
We can now integrate both sides with respect to time t:
∫di=−ε0L∫e−ktdt
This gives:
i=−ε0L⋅(−1ke−kt)+C
where C is the constant of integration. Thus, we have:
i=ε0Lke−kt+C
We know that current i is related to charge q by:
i=dqdt
Substituting for i:
dqdt=ε0Lke−kt+C
Now we can integrate to find the total charge q:
∫dq=∫(ε0Lke−kt+C)dt
This results in:
q=−ε0Lk2e−kt+Ct+Q0
where Q0 is another constant of integration.
Assuming the charge is finite and considering the limits of integration (from t=0 to t=∞), we can evaluate the charge:
q=(−ε0Lk2e−kt)∞0+C(t)∞0
As t→∞, e−kt→0, and at t=0, e−k⋅0=1:
q=−ε0Lk2(0−1)+C(∞−0)
The term with C becomes infinite unless C=0. Thus, we find:
q=ε0Lk2
The total charge that passes a point in the wire of the solenoid is:
q=ε0Lk2
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Multiple Correct Answer
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Comprehension Type
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Subective Type
2 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represent by
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/m and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
View Solution
Knowledge Check
In an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1sIn an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1s
The current in an ideal, long solenoid is varied at a uniform rate of 0.01 As^(-1). The solenoid has 2000 turns/m and its radius 6.0 cm.
(a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. write the change in the magnetic flux through this circle in 2.0 seconds.
(b) find the electric field induced at a point on the circumference of the circle.
(c) find the electric field induced at a point outside the solenoid at a distance 8.0cm from its axis.
View SolutionIf 0.6 mol of electorns flows throutgh a wire in 45 min, what are (a) the total charges that passes through the wire and (b) the magnitude of the current?
View SolutionA uniformly wound long solenoid of inductance L and resistance R is cut into two parts in the ratio η:1, which are then connected in parallel. The combination is then connected to a cell of emf E. The time constant of the circuit is
View SolutionThe diagram shows a solenoid carrying time varying current I=I0t (I0 is constant) on the axis of this solenoid a conducting ring is being placed as shown in the figure. The mutual inductance of the ring and the solenoid is M and self inductance of the ring is L . if the resistance of the ring is R then the maximum current which can flow through the ring is
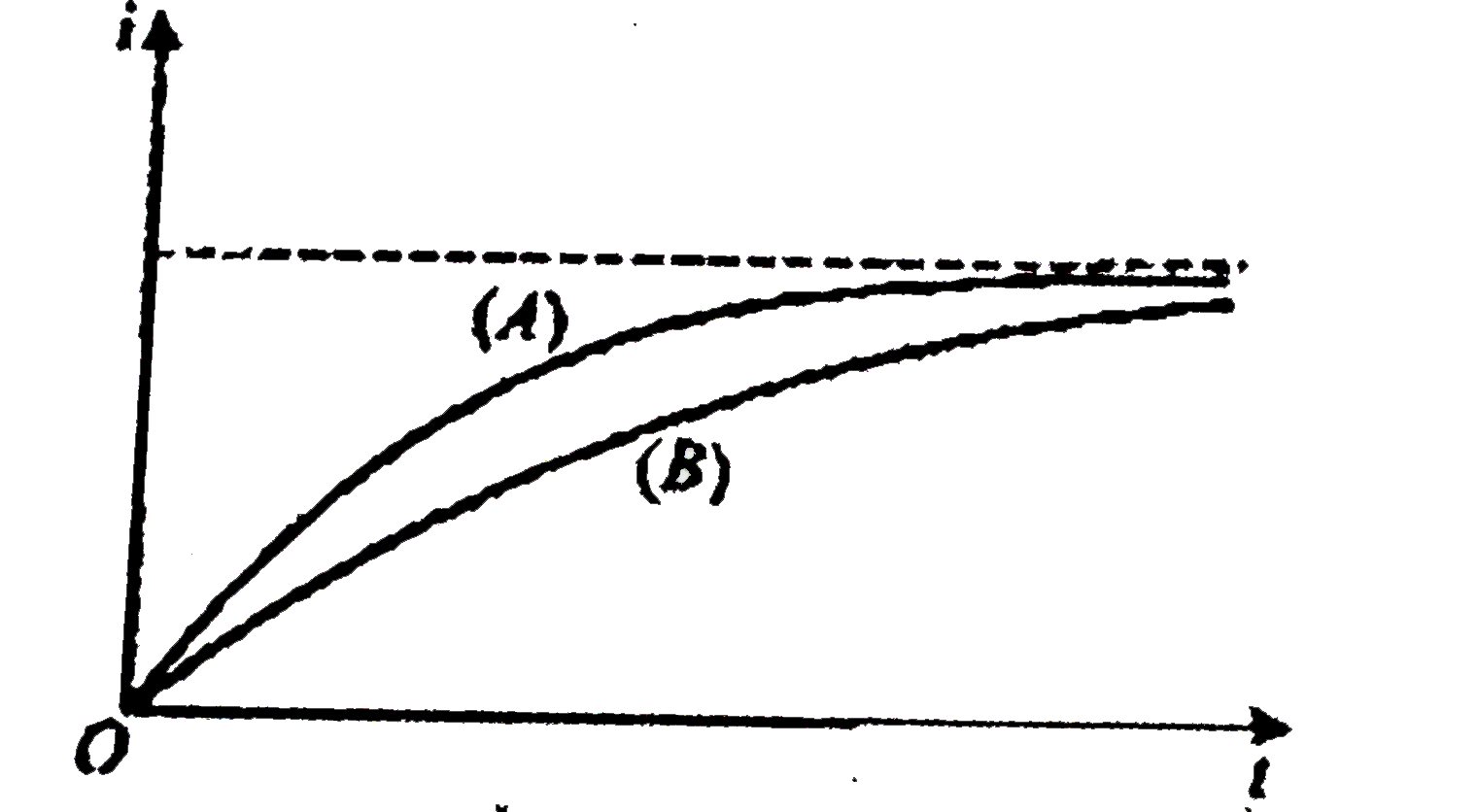
View SolutionA circuit consisting of a constant EMF E, a self-inductance L and a resistance R in sereis is closed at time t=0. The relation between the current i in the circuit and the time t is as shown by the curve. A in the figure-5.321. when one or more of parameters E,R and L are changed, the curve B is obtained. Then it is possible that:
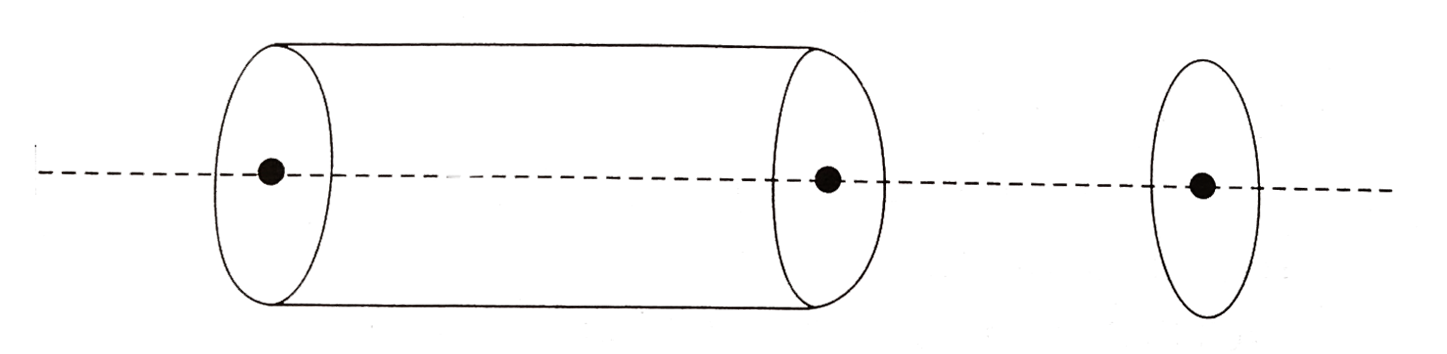
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
View Solution
