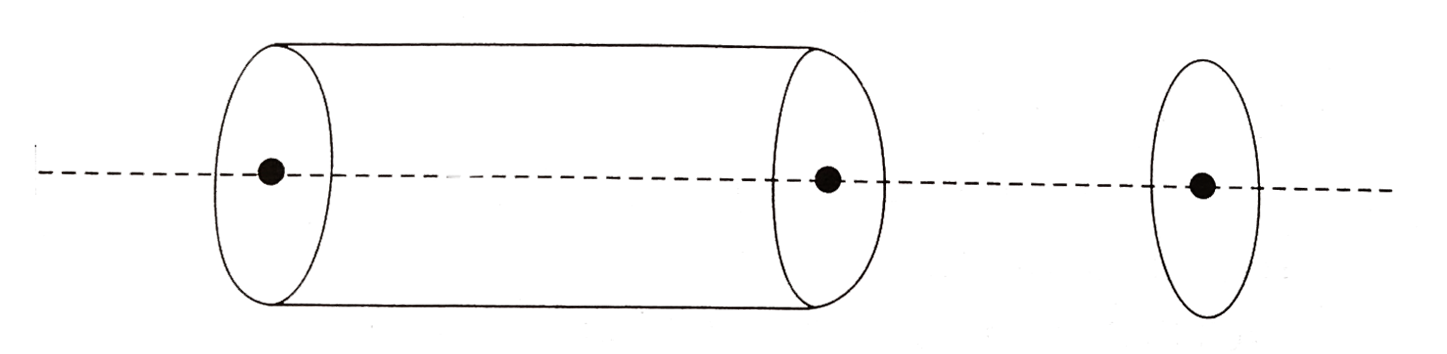
The diagram shows a solenoid carrying time varying current I=I0t (I0 is constant) on the axis of this solenoid a conducting ring is being placed as shown in the figure. The mutual inductance of the ring and the solenoid is M and self inductance of the ring is L . if the resistance of the ring is R then the maximum current which can flow through the ring is
(2M+L)I0R
MI0R
(2M−L)I0R
(M+L)I0R
The correct Answer is:B
To solve the problem, we need to find the maximum current Imax that can flow through the conducting ring placed on the axis of the solenoid carrying a time-varying current I=I0t.
1. Understanding the Current in the Solenoid:
The current in the solenoid is given by:
I(t)=I0t
where I0 is a constant.
2. Finding the Magnetic Flux:
The magnetic flux Φ through the ring due to the solenoid can be expressed as:
Φ=MI(t)
where M is the mutual inductance between the solenoid and the ring.
3. Substituting the Current into the Flux Equation:
Substitute I(t) into the flux equation:
Φ=M(I0t)
4. Calculating the Induced EMF:
According to Faraday's law of electromagnetic induction, the induced EMF E in the ring is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for Φ:
E=−ddt(MI0t)=−MI0
5. Applying Ohm's Law:
According to Ohm's law, the induced EMF is also equal to the product of the current I flowing through the ring and its resistance R:
E=IR
6. Setting the Two Expressions for EMF Equal:
Equating the two expressions for EMF:
−MI0=IR
Since we are interested in the magnitude, we can drop the negative sign:
MI0=IR
7. Solving for the Current I:
Rearranging the equation to find the current I:
I=MI0R
8. Identifying the Maximum Current:
Since the current I is directly proportional to I0 and the mutual inductance M, the maximum current Imax that can flow through the ring is:
Imax=MI0R
Final Answer:
The maximum current which can flow through the ring is:
Imax=MI0R
The current in the solenoid is given by:
I(t)=I0t
where I0 is a constant.
The magnetic flux Φ through the ring due to the solenoid can be expressed as:
Φ=MI(t)
where M is the mutual inductance between the solenoid and the ring.
Substitute I(t) into the flux equation:
Φ=M(I0t)
According to Faraday's law of electromagnetic induction, the induced EMF E in the ring is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for Φ:
E=−ddt(MI0t)=−MI0
According to Ohm's law, the induced EMF is also equal to the product of the current I flowing through the ring and its resistance R:
E=IR
Equating the two expressions for EMF:
−MI0=IR
Since we are interested in the magnitude, we can drop the negative sign:
MI0=IR
Rearranging the equation to find the current I:
I=MI0R
Since the current I is directly proportional to I0 and the mutual inductance M, the maximum current Imax that can flow through the ring is:
Imax=MI0R
The maximum current which can flow through the ring is:
Imax=MI0R
Similar Questions
The diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
 View Solution
View SolutionA magnet is taken towards a conducting ring in such a way that a constant current of 10mA is induced in it. The total resistance of the ring is 0.5Ω. In 5s, the magnetic flux through the ring changes by
View SolutionA magnet is taken towards a conducting ring in such a way that a constant current of 10mA is induced in it. The total resistance of the ring is 0.5Ω. In 5s, the magnetic flux through the ring changes by
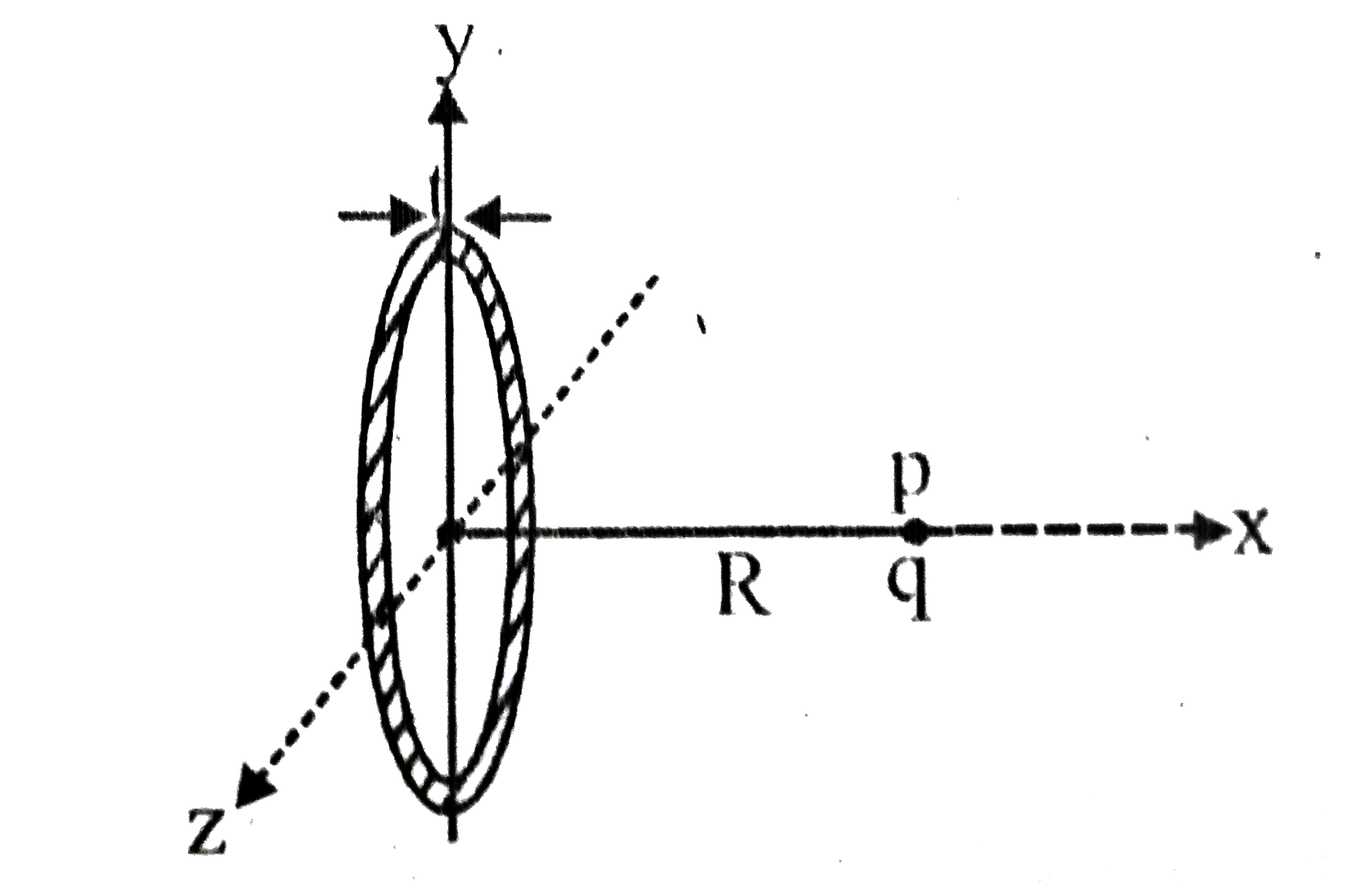
View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
 View Solution
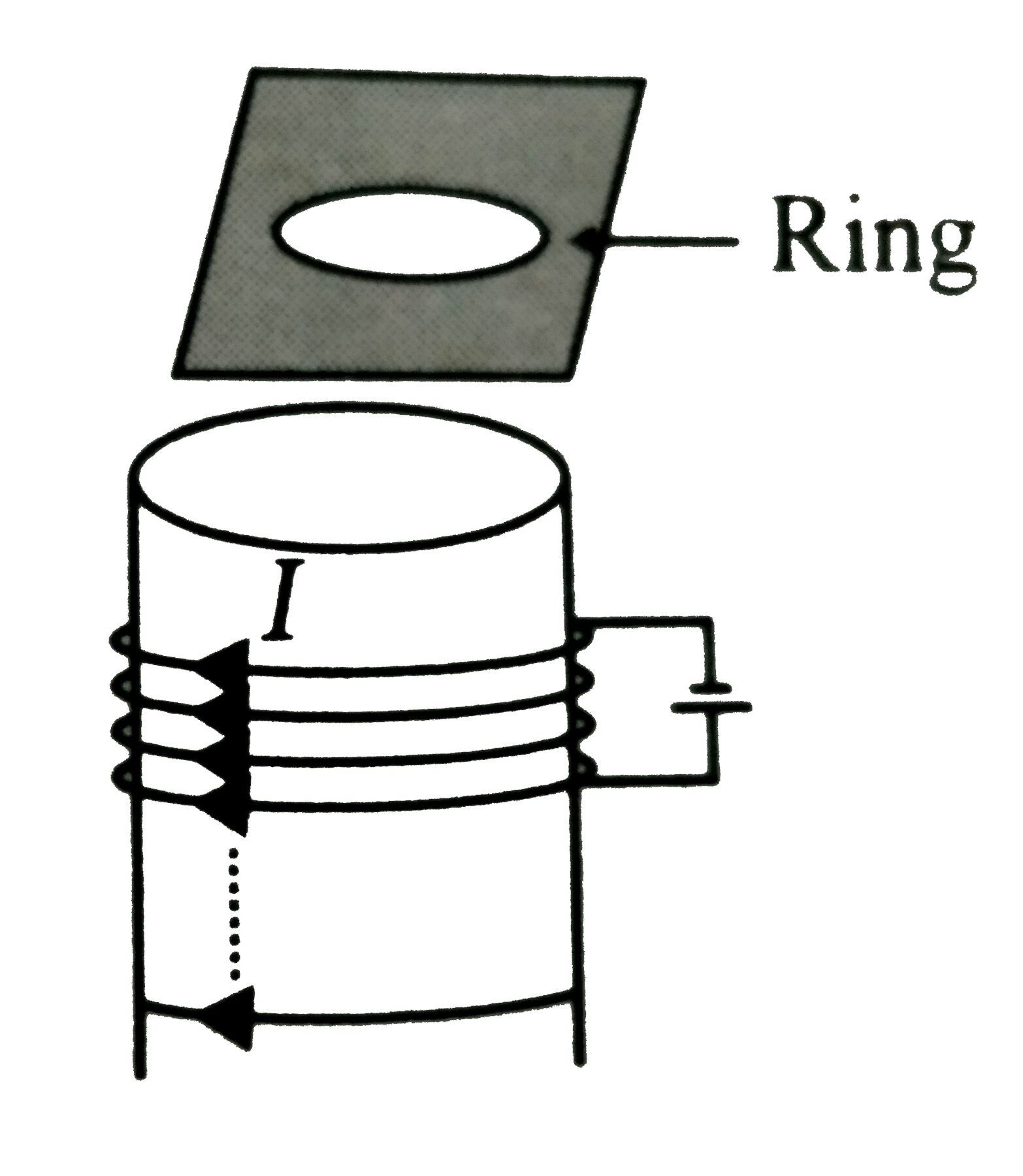
View SolutionA metal ring kept (supported by a card borad) on the top of a fixed soleniod carry a current I as shown in figure. The center of the ring coincides with the axis of the solenoid. If the current in the soleniod is switched off, then
 View Solution
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA short solenoid of length 4 cm, radius 2 cm and 100 turns is placed inside and on the axis of a long solenoid of length 80 cm and 1500 turns. A current of 3 A flows through the short solenoid. The mutual inductance of two solenoid is
View SolutionA long solenoid of radius R carries a time (t)-dependent current I(t)=I0t2(1−t). A conducting ring of radius 3R is placed co-axially near its middle. During the time interva 0≤t≤1, the induced current (IR) in the ring varies as: [Take resistance of ring to be R0]
View SolutionThe figure shows a long straigh wire carryhing a current I1 along the axis of a circular ring carrying a current I_2. Identify the correct statement.
 View Solution
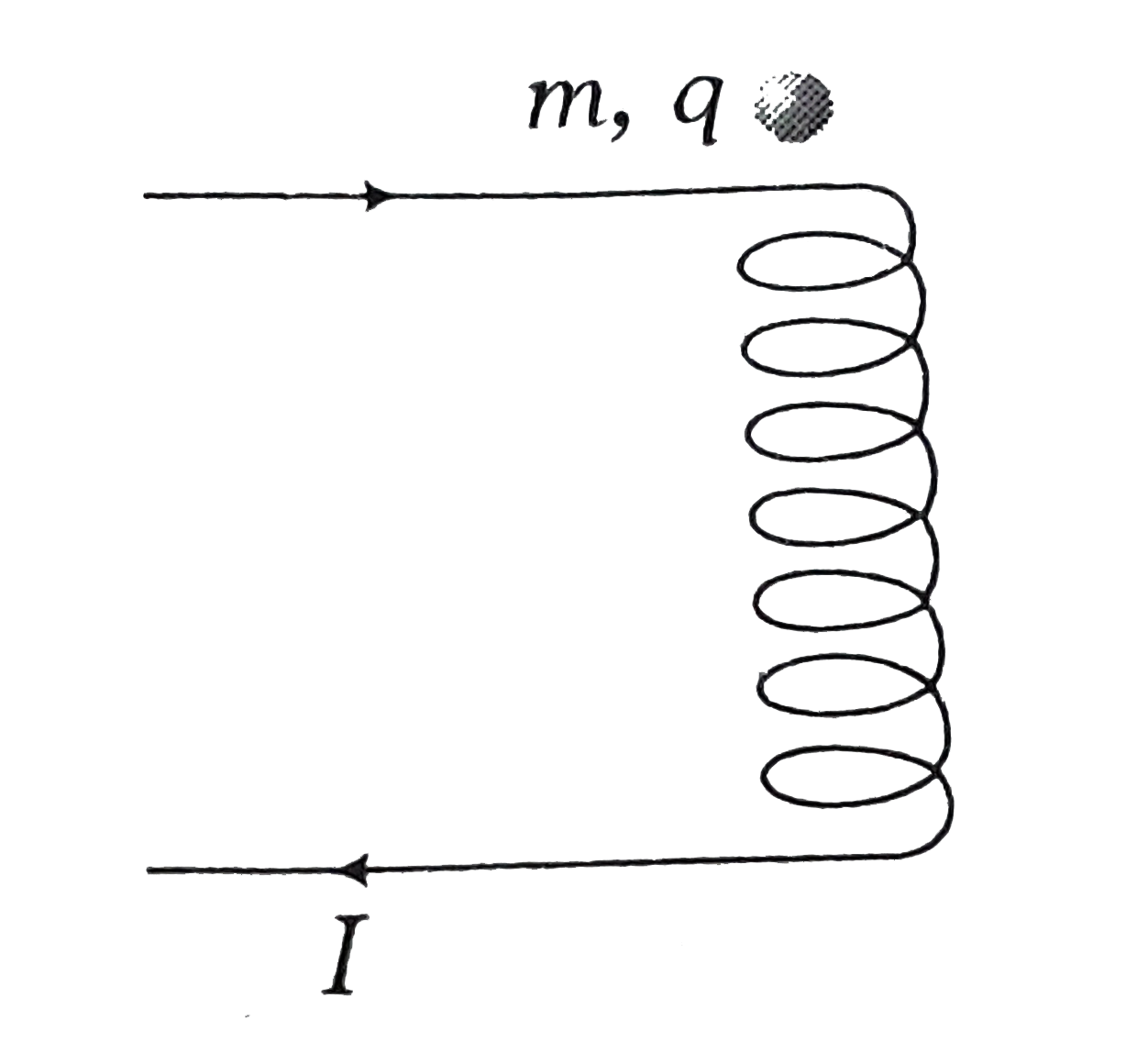
View SolutionA long solenoid carrying a current I is placed with its axis vertical as shown in the figure. A particle of mass m and charge q is released from the top of the solenoid. Its acceleration is (g being acceleration due to gravity)
 View Solution
View Solution
