Discuss the similarities between the energy stored in the electric field of charged capacitor and the energy stored in the magnetic field of a current-carrying coil.
To discuss the similarities between the energy stored in the electric field of a charged capacitor and the energy stored in the magnetic field of a current-carrying coil, we can follow these steps:
Step 1: Understand the Energy Stored in a Capacitor
The energy (U) stored in a capacitor can be expressed using the formula:
U=12CV2
where:
- U is the energy stored,
- C is the capacitance of the capacitor,
- V is the voltage across the capacitor.
Step 2: Understand the Energy Stored in an Inductor
The energy (U) stored in an inductor can be expressed using the formula:
U=12LI2
where:
- U is the energy stored,
- L is the inductance of the coil,
- I is the current flowing through the coil.
Step 3: Identify the Proportional Relationships
From the formulas derived:
- The energy stored in a capacitor is directly proportional to the square of the voltage (V2) and the capacitance (C).
- The energy stored in an inductor is directly proportional to the square of the current (I2) and the inductance (L).
Step 4: Compare the Energy Storage Mechanisms
Both energy storage mechanisms involve:
- A quadratic relationship: Both energies are proportional to the square of a variable (voltage for capacitors and current for inductors).
- Dependence on a geometric factor: The energy stored in a capacitor depends on its capacitance, while the energy stored in an inductor depends on its inductance.
Step 5: Conclude the Similarities
In conclusion, both the energy stored in the electric field of a capacitor and the energy stored in the magnetic field of a coil share the following similarities:
- Both energies are stored in fields (electric and magnetic).
- Both depend on the square of a fundamental quantity (voltage or current).
- Both depend on a geometric property of the device (capacitance for capacitors and inductance for inductors).
The energy (U) stored in a capacitor can be expressed using the formula:
U=12CV2
where:
- U is the energy stored,
- C is the capacitance of the capacitor,
- V is the voltage across the capacitor.
The energy (U) stored in an inductor can be expressed using the formula:
U=12LI2
where:
- U is the energy stored,
- L is the inductance of the coil,
- I is the current flowing through the coil.
From the formulas derived:
- The energy stored in a capacitor is directly proportional to the square of the voltage (V2) and the capacitance (C).
- The energy stored in an inductor is directly proportional to the square of the current (I2) and the inductance (L).
Both energy storage mechanisms involve:
- A quadratic relationship: Both energies are proportional to the square of a variable (voltage for capacitors and current for inductors).
- Dependence on a geometric factor: The energy stored in a capacitor depends on its capacitance, while the energy stored in an inductor depends on its inductance.
In conclusion, both the energy stored in the electric field of a capacitor and the energy stored in the magnetic field of a coil share the following similarities:
- Both energies are stored in fields (electric and magnetic).
- Both depend on the square of a fundamental quantity (voltage or current).
- Both depend on a geometric property of the device (capacitance for capacitors and inductance for inductors).
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Comprehension Type
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Knowledge Check
The energy stored in an electric cell is
Achemical energyBelectrical energyCheat energyDmechanical energy
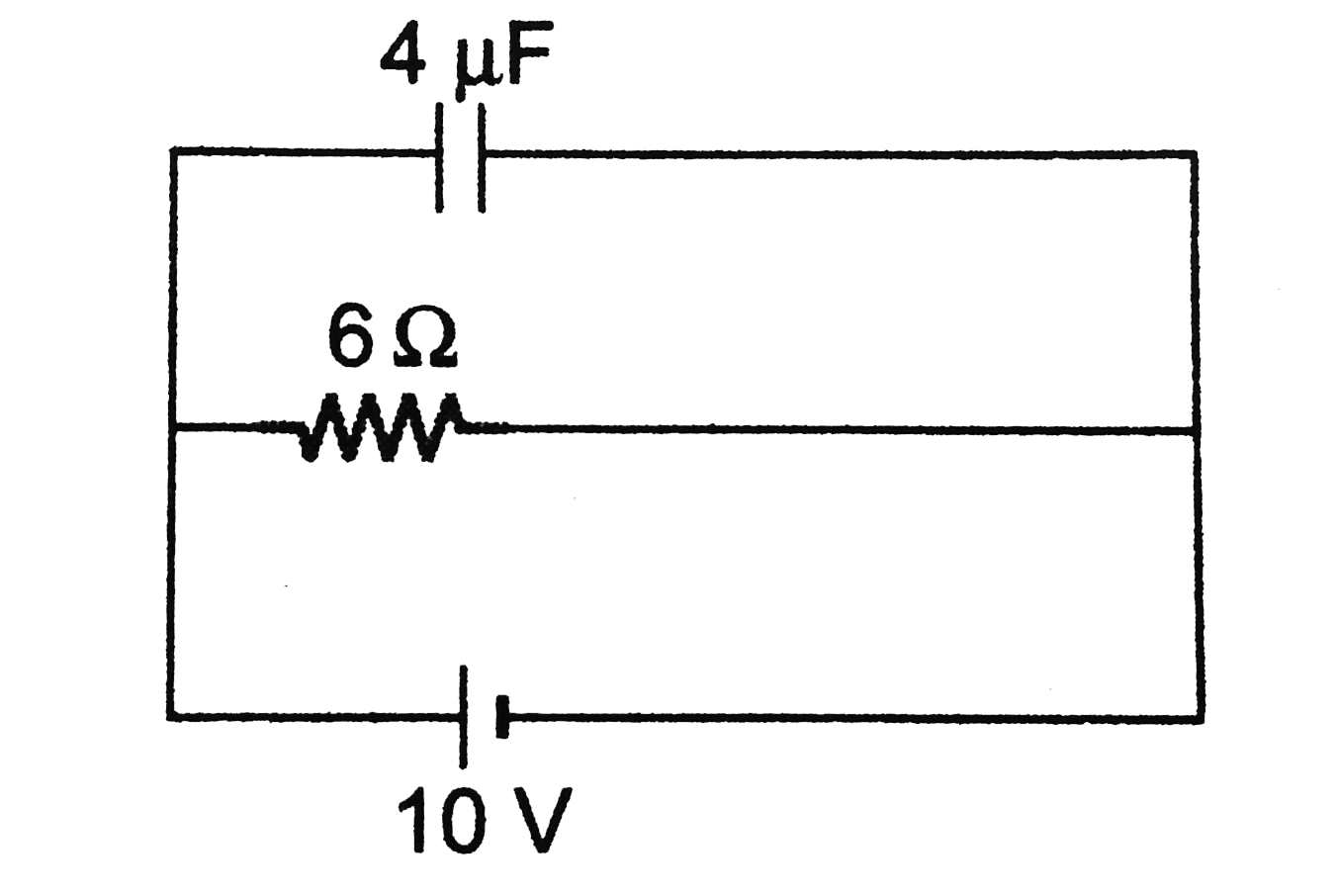
The energy stored in 4μF capacitors is
View SolutionFind the charge stored in the capacitor.
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
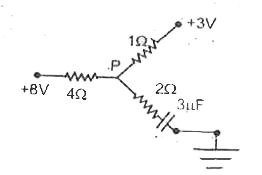
View SolutionThe energy stored in the capacitor in the steady state is
View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View SolutionFind the energy stored in the electirc field produced by a metal sphere of radius R containing a charge Q.
View SolutionMatch the columns

View Solution

