A 1.00μF capacitor is charged by a 40.0V power supply. The fully charged charged capacitor is then discharged through a 10.0mH inductor. Find the maximum current in the resultaing oscillations.
400mA
800mA
600mA
150mA
The correct Answer is:A
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the maximum charge on the capacitor
The maximum charge Q on a capacitor is given by the formula:
Q=C×V
where:
- C=1.00μF=1.00×10−6F
- V=40.0V
Substituting the values:
Q=(1.00×10−6F)×(40.0V)=40.0×10−6C
Thus, the maximum charge Q is:
Q=40.0μC
Step 2: Calculate the angular frequency of the LC circuit
The angular frequency ω of an LC circuit is given by:
ω=1√L×C
where:
- L=10.0mH=10.0×10−3H
- C=1.00×10−6F
Substituting the values:
ω=1√(10.0×10−3H)×(1.00×10−6F)
Calculating the product inside the square root:
=1√10.0×10−9=1√10−8=110−4=10,000rad/s
Step 3: Calculate the maximum current in the oscillations
The maximum current Imax in the oscillations can be calculated using the formula:
Imax=ω×Q
Substituting the values:
Imax=(10,000rad/s)×(40.0×10−6C)
Calculating this gives:
Imax=10,000×40.0×10−6=400×10−3A=0.400A=400mA
Final Result
The maximum current in the resulting oscillations is:
Imax=400mA
The maximum charge Q on a capacitor is given by the formula:
Q=C×V
where:
- C=1.00μF=1.00×10−6F
- V=40.0V
Q=(1.00×10−6F)×(40.0V)=40.0×10−6C
Thus, the maximum charge Q is:
Q=40.0μC
The angular frequency ω of an LC circuit is given by:
ω=1√L×C
where:
- L=10.0mH=10.0×10−3H
- C=1.00×10−6F
ω=1√(10.0×10−3H)×(1.00×10−6F)
Calculating the product inside the square root:
=1√10.0×10−9=1√10−8=110−4=10,000rad/s
The maximum current Imax in the oscillations can be calculated using the formula:
Imax=ω×Q
Imax=(10,000rad/s)×(40.0×10−6C)
Calculating this gives:
Imax=10,000×40.0×10−6=400×10−3A=0.400A=400mA
The maximum current in the resulting oscillations is:
Imax=400mA
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Comprehension Type
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Knowledge Check
A charged 30 μF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit ?
A1.1×103rad s−1B2.1×103rad s−1C3.1×103rad s−1D4.1×103rad s−1A 1.5μF capacitor is charged of 60 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Assuming that the circuit contains no resistance, the maximum current in this coil shall be close to
A1.4AB1.2AC0.8AD0.6A
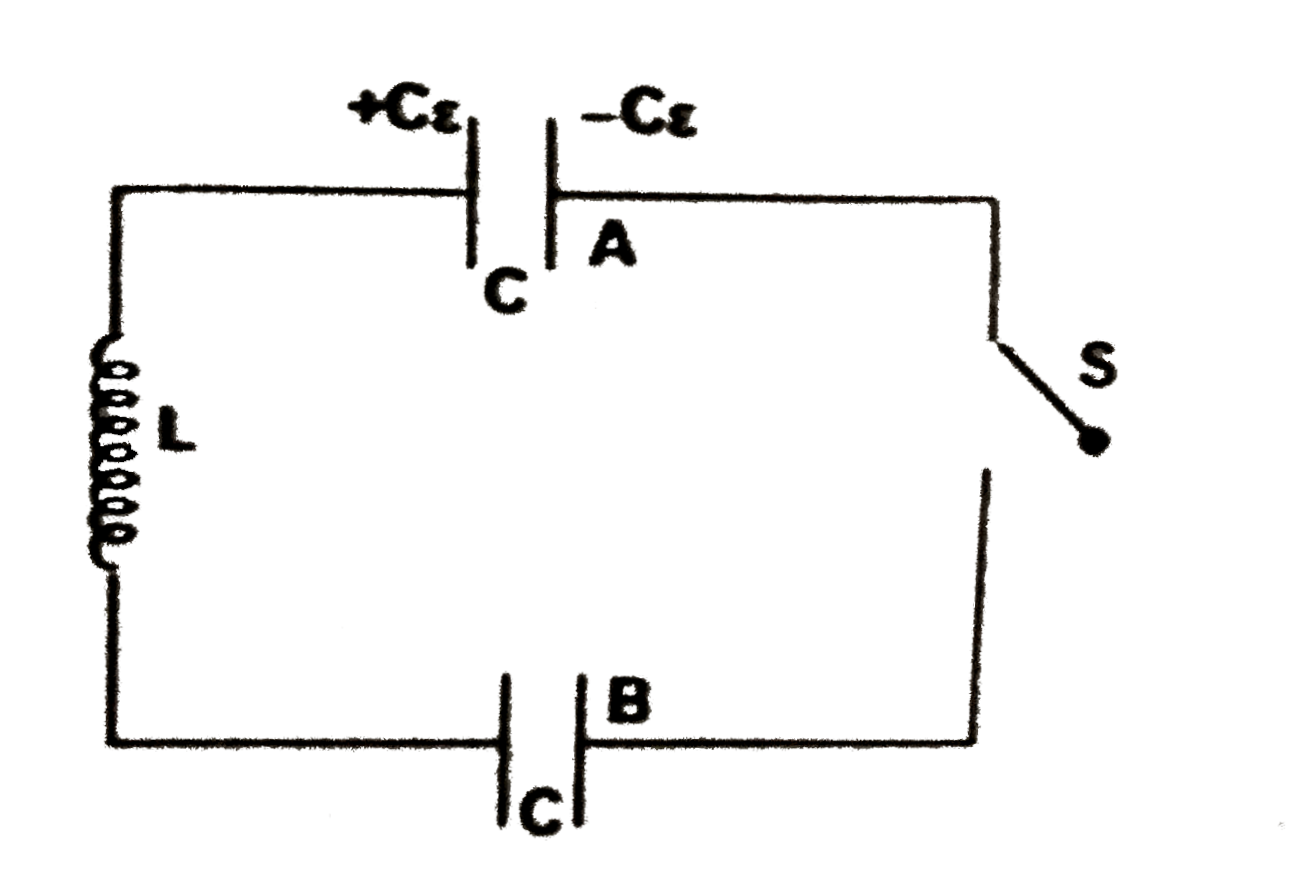
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?

View SolutionA 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
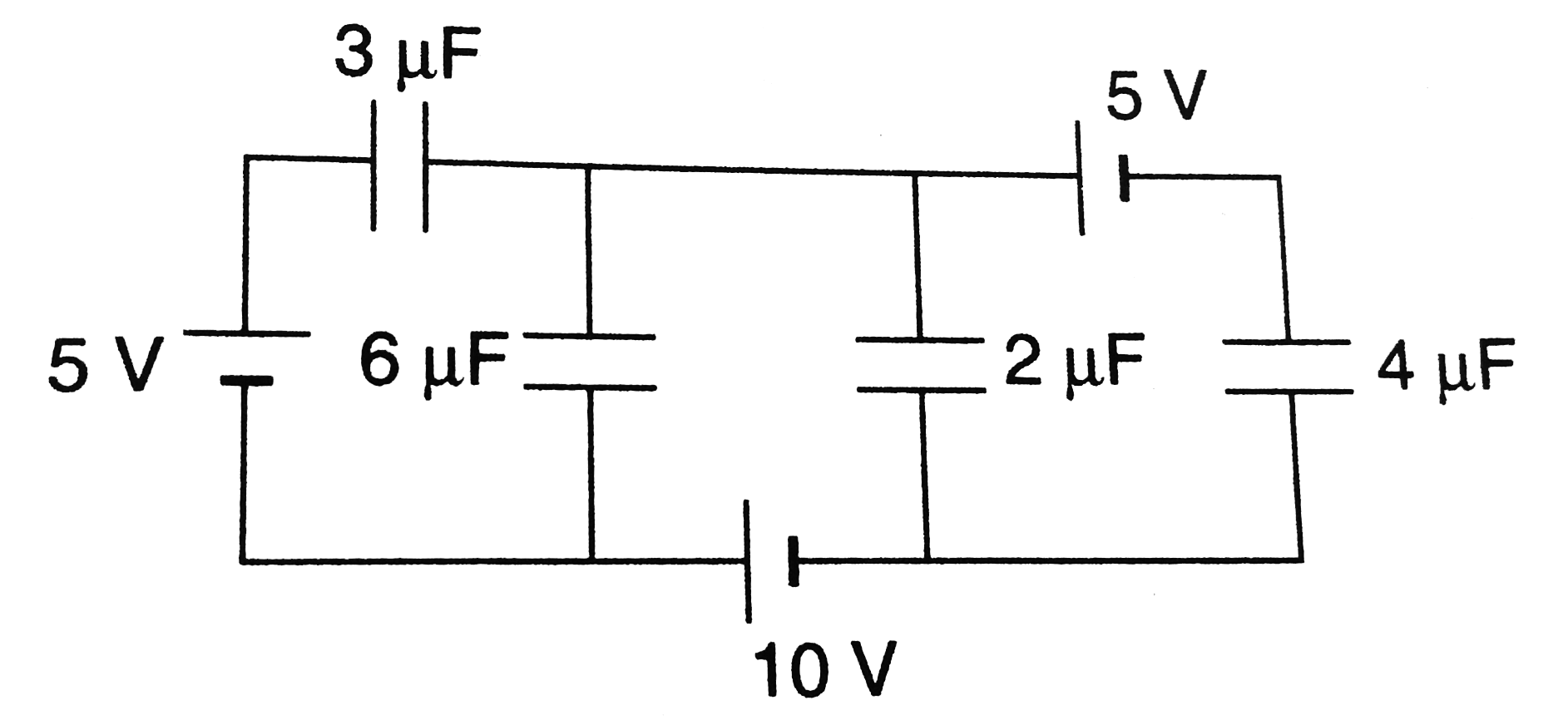
View SolutionFind the charges on 6μF and 4μF capacitors
View SolutionA 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking at the instant at which inductor is connected to the capacitor at t = 0
View Solution
