A ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
The correct Answer is:D
To solve the problem, we need to determine the maximum base angle (α) of a right-angled prism for which light is totally reflected from the hypotenuse when the light ray travels parallel to the base of the prism.
1. Understanding the Geometry of the Prism:
- We have a right-angled prism where one angle is 90 degrees (the right angle).
- Let the base angle be α. Therefore, the other angle (the angle at the hypotenuse) will be (90 - α).
2. Ray of Light Incident on the Hypotenuse:
- A ray of light travels parallel to the base of the prism and strikes the hypotenuse.
- When the light ray strikes the hypotenuse, we need to analyze the angles involved.
3. Using Snell's Law:
- According to Snell's law, at the boundary between two media, we have:
μ1sin(θ1)=μ2sin(θ2)
- Here, µ is the refractive index of the prism, and we can assume the refractive index of air (µ1) is 1.
- The angle of incidence (θ1) at the hypotenuse will be (90 - α) because the light is traveling parallel to the base.
4. Setting Up the Equation:
- At the hypotenuse, we can write:
1⋅sin(90∘)=μ⋅sin(90−α)
- Since sin(90°) = 1, we have:
1=μ⋅cos(α)
5. Solving for α:
- Rearranging the equation gives:
cos(α)=1μ
- To find α, we take the inverse cosine:
α=cos−1(1μ)
6. Conclusion:
- The maximum value of the base angle α for which light is totally reflected from the hypotenuse is:
α=cos−1(1μ)
Final Answer:
The maximum value of the base angle for which light is totally reflected from the hypotenuse is:
α=cos−1(1μ)
- We have a right-angled prism where one angle is 90 degrees (the right angle).
- Let the base angle be α. Therefore, the other angle (the angle at the hypotenuse) will be (90 - α).
- A ray of light travels parallel to the base of the prism and strikes the hypotenuse.
- When the light ray strikes the hypotenuse, we need to analyze the angles involved.
- According to Snell's law, at the boundary between two media, we have:
μ1sin(θ1)=μ2sin(θ2)
- Here, µ is the refractive index of the prism, and we can assume the refractive index of air (µ1) is 1.
- The angle of incidence (θ1) at the hypotenuse will be (90 - α) because the light is traveling parallel to the base.
- At the hypotenuse, we can write:
1⋅sin(90∘)=μ⋅sin(90−α)
- Since sin(90°) = 1, we have:
1=μ⋅cos(α)
- Rearranging the equation gives:
cos(α)=1μ
- To find α, we take the inverse cosine:
α=cos−1(1μ)
- The maximum value of the base angle α for which light is totally reflected from the hypotenuse is:
α=cos−1(1μ)
The maximum value of the base angle for which light is totally reflected from the hypotenuse is:
α=cos−1(1μ)
Topper's Solved these Questions
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.4
15 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
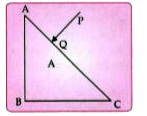
A ray of light PQ is incident normally on the hypotenuse of a right angled prism ABC as shown in the diagram given below:
What is the value of the angle of deviation of the ray ?
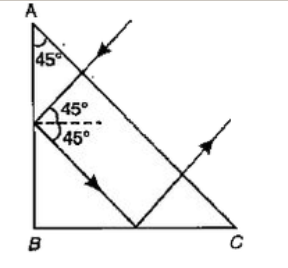
View SolutionA ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
View Solution
Knowledge Check
A ray of light is incident at small angle I on the surface of prism of small angle A and emerges normally from the oppsite surface. If the refractive index of the material of the prism is mu, the angle of incidence is nearly equal to
AAμBA2μCμADμA2
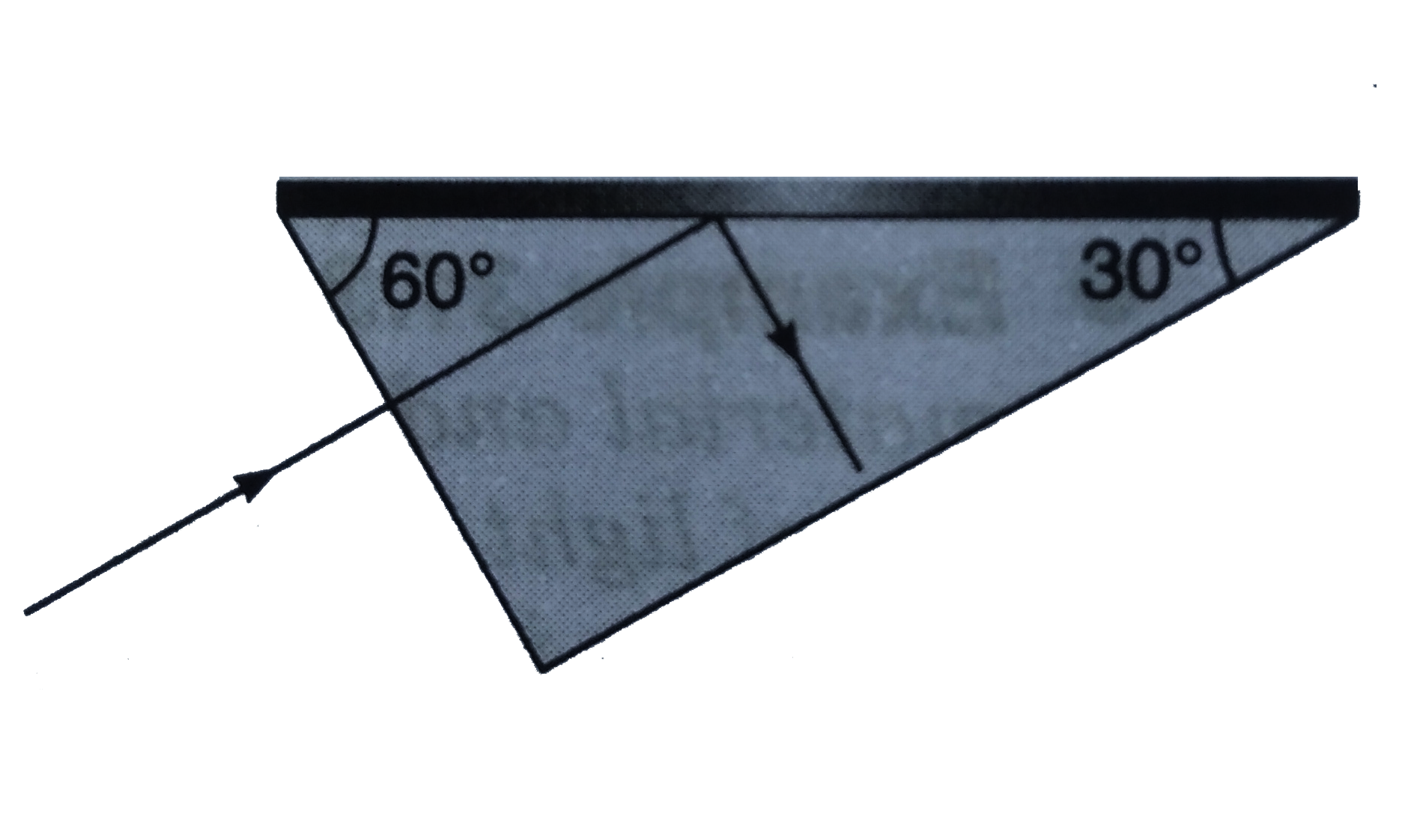
Light is incident normally on the short face of a 30∘−60∘−90∘ prism. A liquid is poured on the hypotenuse of the prism. If the refractive index of the prism is √3, find the maximum refractive index of the liquid so that light is totally reflected.
View SolutionA ray of light is incident at small angle I on the surface of prism of small angle A and emerges normally from the oppsite surface. If the refractive index of the material of the prism is mu, the angle of incidence is nearly equal to
View SolutionA ray of light is incident at small angle I on the surface of prism of small angle A and emerges normally from the oppsite surface. If the refractive index of the material of the prism is mu, the angle of incidence is nearly equal to
View SolutionA ray of light PQ is incident normally on the hypotenuse of a right angled prism ABC as shown in the diagram given below:
Name an instrument where this action of the prism is used.
View SolutionA ray of light PQ is incident normally on the hypotenuse of a right angled prism ABC as shown in the diagram.

Name an instrument where this action of the prism is used.
View SolutionA ray of light incident on an equilateral triangular glass prism of μ=√3 moves parallel to the base of the prism inside it. What is the angle of incidence for this ray ?
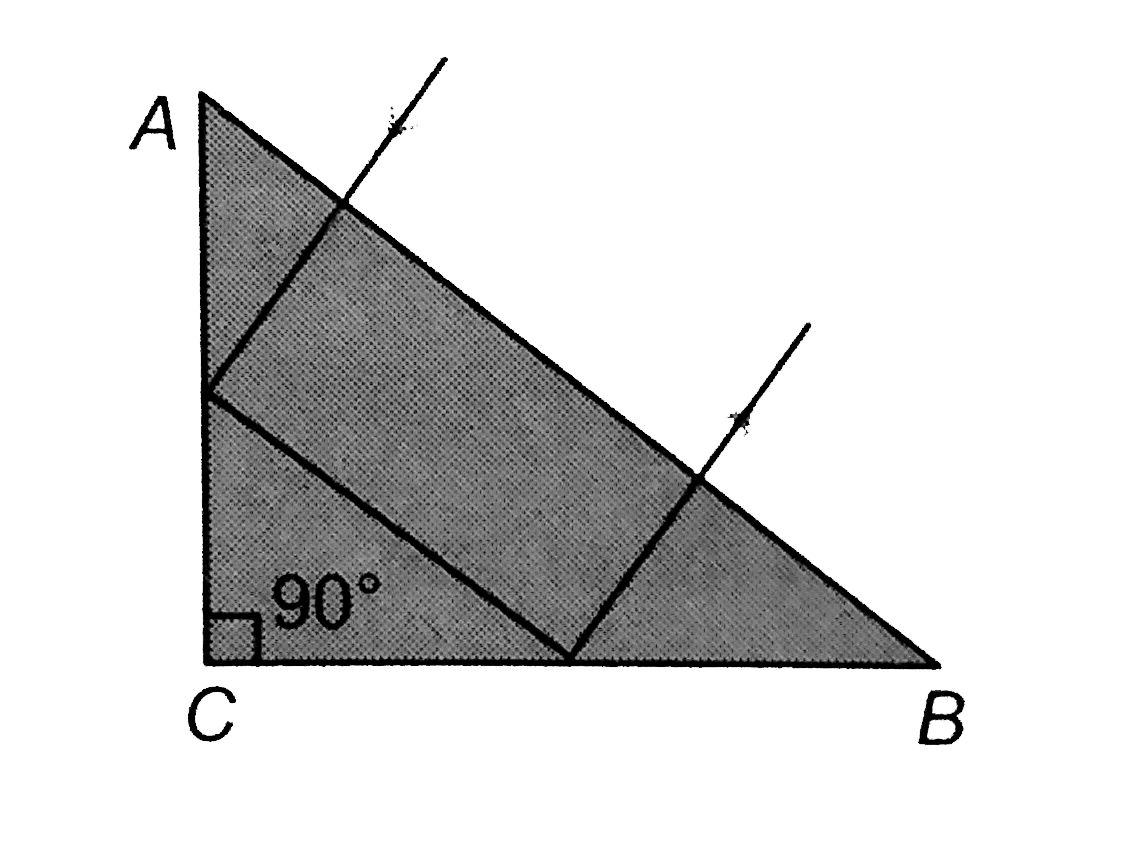
View SolutionA ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be
View Solution
