In a biprism experiement, by using light of wavelength 5000Å, 5mm wide fringes are obtained on a screen 1.0m away from the coherent sources. The separation between the two coherent sources is
1.0 mm
0.1 mm
0.05 mm
0.01 m
The correct Answer is:B
To solve the problem, we need to find the separation between the two coherent sources in a biprism experiment using the given parameters.
1. Identify the Given Values:
- Wavelength of light, λ=5000Å=5000×10−10m
- Fringe width, β=5mm=5×10−3m
- Distance from the biprism to the screen, D=1.0m
2. Use the Formula for Fringe Width:
The formula for fringe width in a biprism experiment is given by:
β=Dλd
where d is the separation between the two coherent sources.
3. Rearrange the Formula to Solve for d:
We can rearrange the formula to find d:
d=Dλβ
4. Substitute the Known Values:
Now, substitute the values into the equation:
d=1.0m×(5000×10−10m)5×10−3m
5. Calculate the Separation d:
Performing the calculation:
d=1.0×5000×10−105×10−3=5000×10−105×10−3=50005×10−10+3=1000×10−7=0.1×10−3m
6. Convert to Millimeters:
Convert the result to millimeters:
d=0.1mm
7. Final Result:
The separation between the two coherent sources is 0.1mm.
Conclusion:
The correct answer is 0.1mm.
- Wavelength of light, λ=5000Å=5000×10−10m
- Fringe width, β=5mm=5×10−3m
- Distance from the biprism to the screen, D=1.0m
The formula for fringe width in a biprism experiment is given by:
β=Dλd
where d is the separation between the two coherent sources.
We can rearrange the formula to find d:
d=Dλβ
Now, substitute the values into the equation:
d=1.0m×(5000×10−10m)5×10−3m
Performing the calculation:
d=1.0×5000×10−105×10−3=5000×10−105×10−3=50005×10−10+3=1000×10−7=0.1×10−3m
Convert the result to millimeters:
d=0.1mm
The separation between the two coherent sources is 0.1mm.
The correct answer is 0.1mm.
Similar Questions
In Young’s double slit experiment, using light of wavelength 600 nm, 10th bright fringe is obtained on a screen, 3mm from the centre of the pattern. If the screen is 120 cm away from the slits, calculate:
(i) Distance between the two slits,
(ii) Fringe width, i.e. fringe separation.
View SolutionTwo coherent source of light can be obtained by
View SolutionIn Young.s double slit experiment, blue-green light of wavelength 500nm is used. The slits are 1.20mm apart, and the viewing screen is 5.40m away from the slits. What is the fringe width.
View SolutionTwo slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
View SolutionIn a Young's double slit experiment the separation between the slits is 0.10 mm, the wavelength of light used is 600 nm and the interference pattern is observed on a screen 1.0 m away. Find the separation between the successive bright fringes.
View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
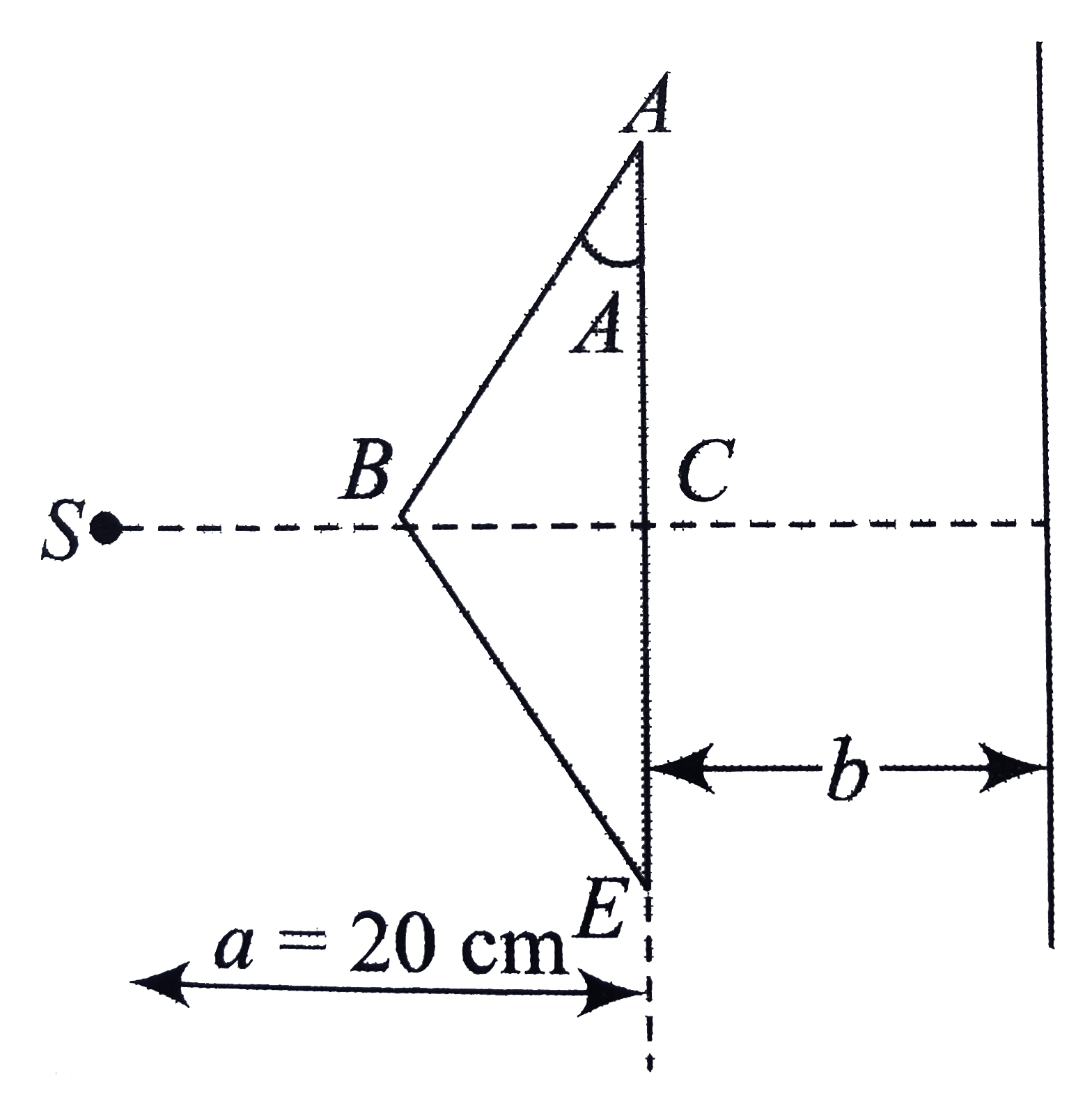
View SolutionTwo small angled transparent prisms (each or refracting angle A=1∘) are so placed that their bases coincide, so that common base is BC. This device is called Fresnel's biprism and is used to obtain coherent sources of a point source S illuminated by monochromatic light of wavelength 6000Å placed at a distance a=20 cm. Calculate the separation between coherent sources. If a screen is placed at a distance b=80 cm. from the device, what ist the finge which of fringes obtained (Refractive index of material of each prism =1.5.)
View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View SolutionIn young's double slit experiment with monochromic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 cm towards the slits, then the change in fringe width is 30μm if the distance between the slits is 1mm, then calculate wavelength of the light used.
View SolutionIn Young's double slit experiment slits are separated by 2 mm and the screen is placed at a distance of1.2 m from the slits. Light consisting of two wavelengths 6500Å and 5200Å are used to obtain interference fringes.
The the separation between the fourth bright fringes the two wavelength is
View Solution
